模板：数论 & 数论函数 & 莫比乌斯反演

作为神秘奖励……？也是为了方便背。

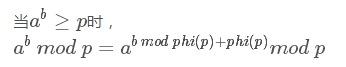
所有的除法都是向下取整。

数论函数：

\((f*g)(n)=\sum_{d|n}f(d)g(\frac{n}{d})\)

\((Id*\mu)(n)=\sum_{d|n}\mu(d)\frac{n}{d}=\phi(n)\)

筛法求积性函数：

int su[N],he[N],miu[N],phi[N],c[N],d[N],tot;
void Euler(int n){
    miu[1]=d[1]=c[1]=phi[1]=1;
    for(int i=2;i<=n;i++){
		if(!he[i]){
		    su[++tot]=i;
		    miu[i]=-1;
		    phi[i]=i-1;
		    d[i]=2;
		    c[i]=1;
		}
		for(int j=1;j<=tot;j++){
		    int p=su[j];
		    if(i*p>n)break;
		    he[i*p]=1;
		    if(i%p==0){
				miu[i*p]=0;
				phi[i*p]=phi[i]*p;
				d[i*p]=d[i]/(c[i]+1)*(c[i]+2);
				c[i*p]=c[i]+1;
				break;
		    }else{
				miu[i*p]=miu[i]*miu[p];
				phi[i*p]=phi[i]*phi[p];
				d[i*p]=d[i]*d[p];
				c[i*p]=1;
		    }
		}
    }
}

莫比乌斯反演：

\(n=\sum_{d|n}\phi(d)\)

\([n=1]=\sum_{d|n}\mu(d)\)

推导：

\(\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j)=p]=\sum_{d=1}^{min(\frac{n}{p},\frac{m}{p})}\mu(d)*\frac{\frac{n}{p}}{d}*\frac{\frac{m}{p}}{d}\)

例题+推导：BZOJ1101 & 洛谷3455：[POI2007]ZAP

\(\sum_{i=1}^n\sum_{j=1}^mgcd(i,j)=\sum_{d=1}^{min(n,m)}\phi(d)*\frac{n}{d}*\frac{m}{d}\)

例题+推导：BZOJ2005：[Noi2010]能量采集

\(\sum_{i=1}^n\sum_{j=1}^mlcm(i,j)=\sum_{k=1}^{min(n,m)}sum(\frac{n}{k})sum(\frac{m}{k})\sum_{d|k}d^2\mu(d)\frac{k}{d}\)

例题+推导：BZOJ2693：jzptab——题解

杜教筛：

令\(M(n)=∑_{i=1}^nμ(i)\)

则\(M(n)=1−∑_{i=2}^nM(\frac{n}{i})\)

令\(S(n)=∑_{i=1}^n\phi(i)\)

则\(S(n)=∑_{i=1}^ni−∑_{i=2}^nS(\frac{n}{i})\)

推导：http://blog.csdn.net/samjia2000/article/details/70147436



+++++++++++++++++++++++++++++++++++++++++++

+本文作者：luyouqi233。 　　　　　　　　　　　　　　+

+欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/ +

+++++++++++++++++++++++++++++++++++++++++++