【LabVIEW技巧】策略模式
前言
为什么学习OOP


简单工厂模式
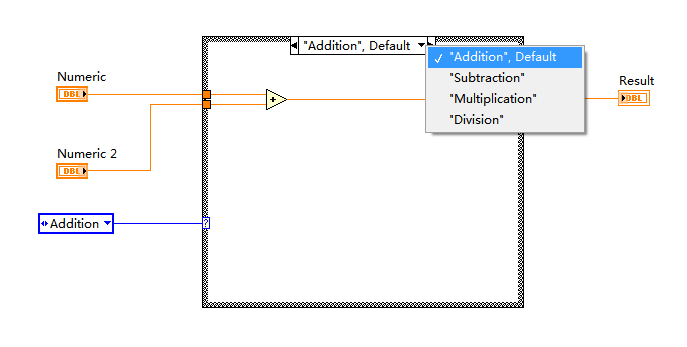
但是当多个函数中都需要进行判断时,Case结构将会写很多个,并且每一次维护代码均需要了解之前的设计,极易造成误修改。
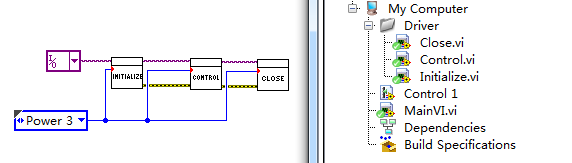
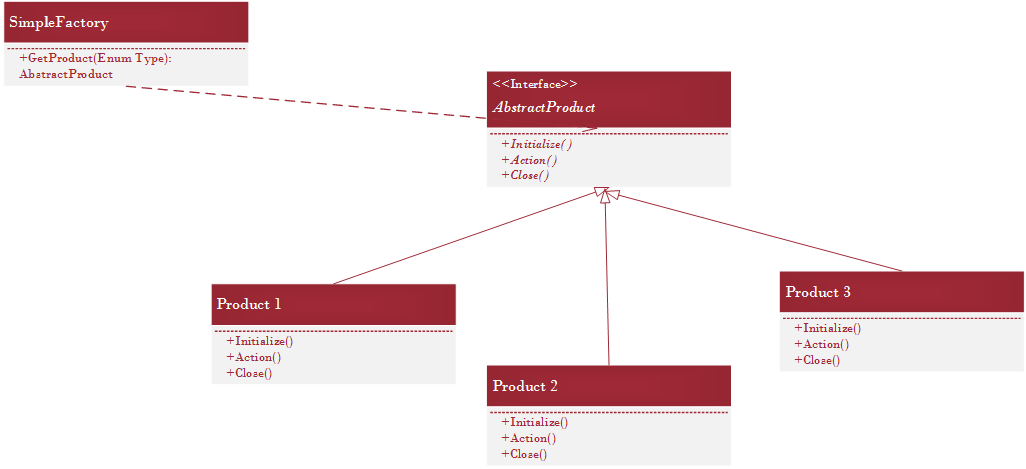
了解UML类图,可以发现程序在运行时动态选择执行的内容,通过类的继承,可以实现对原有方法的轻易拓展;改动的时候不影响主程序的原有设计,实现了针对接口而不是实现编程。
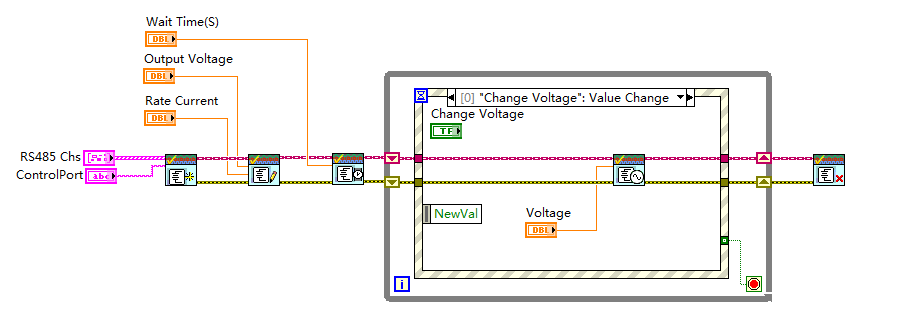
策略模式
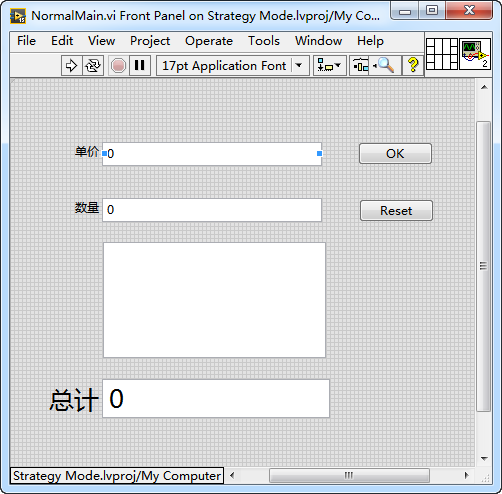
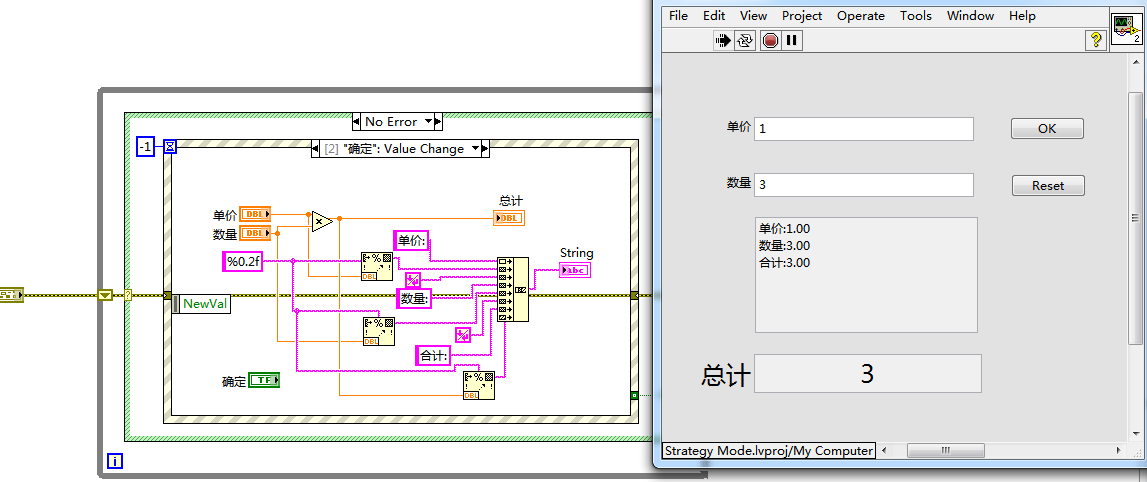
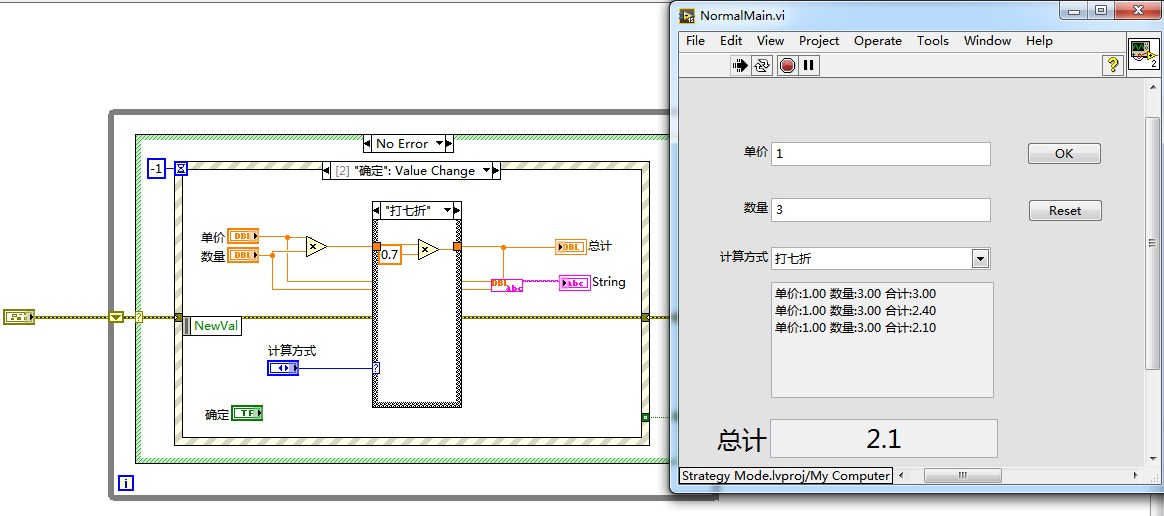
简单工厂实现
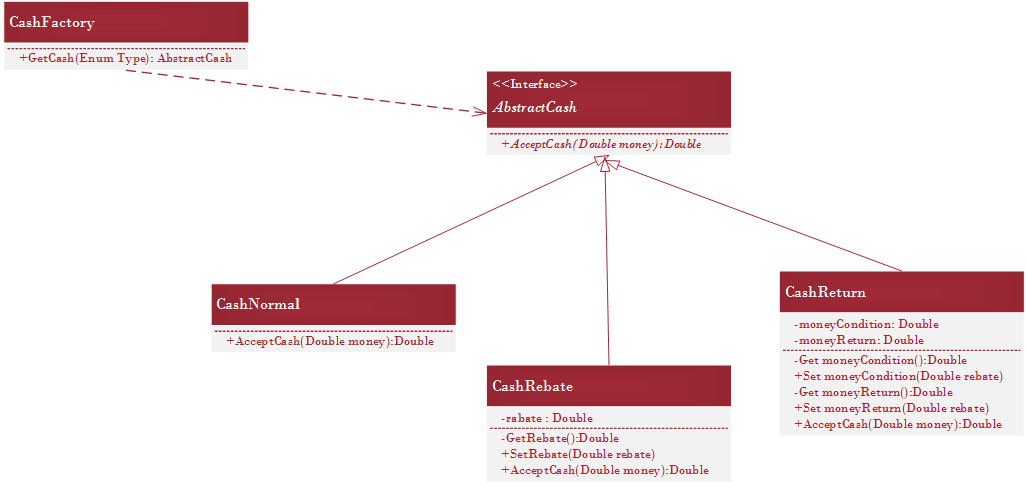
算法抽象
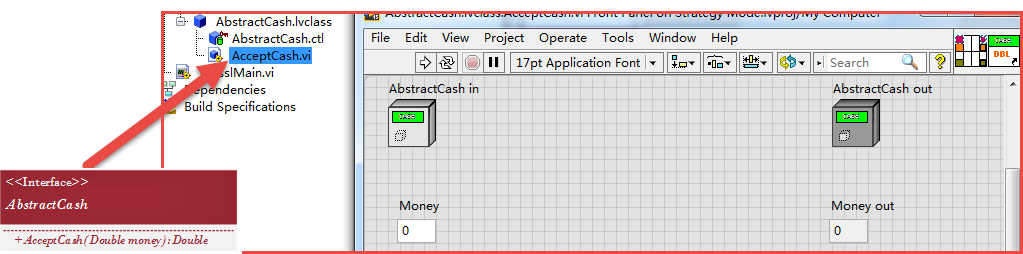
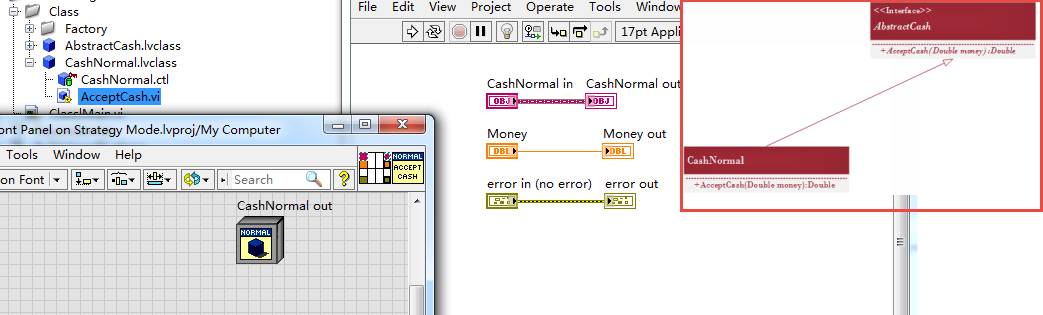
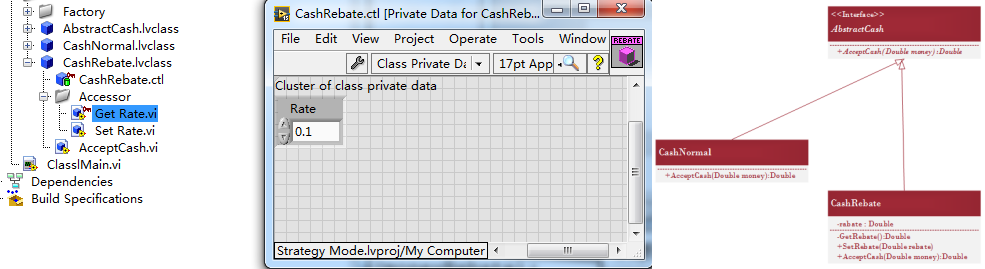
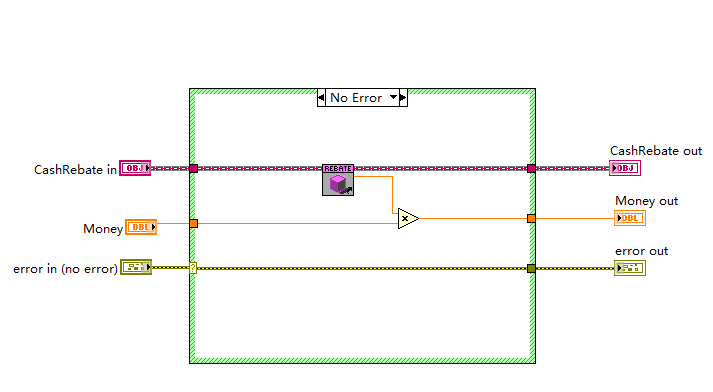
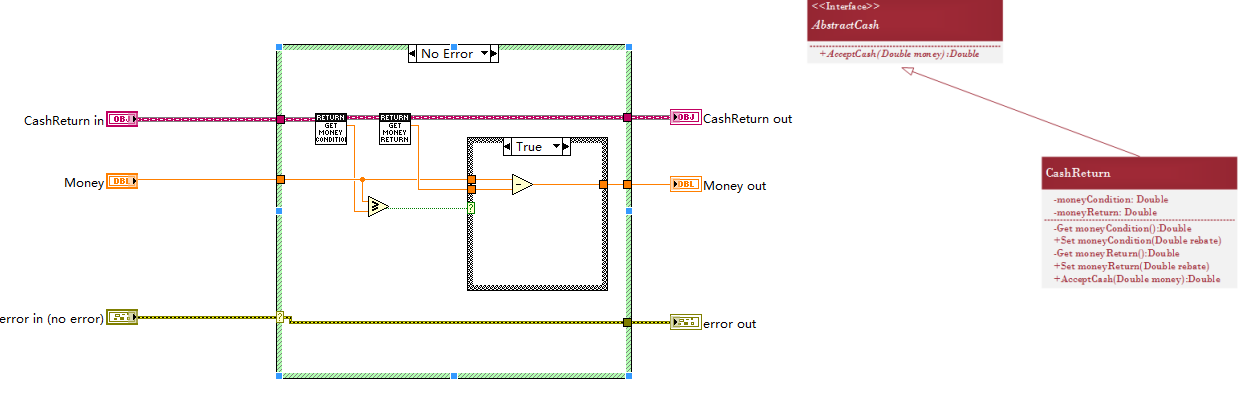
工厂设计
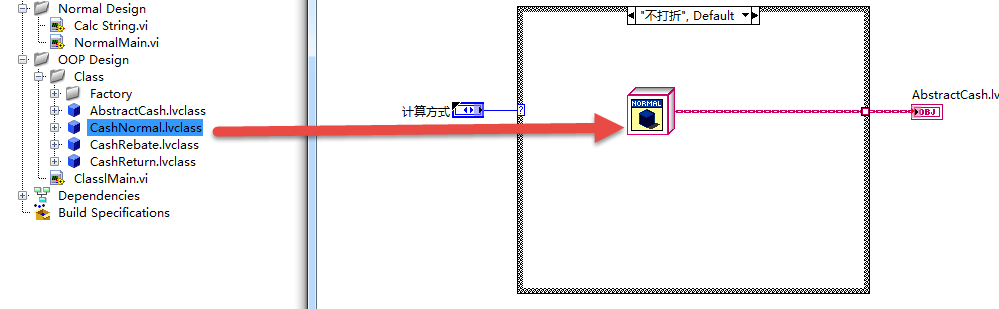
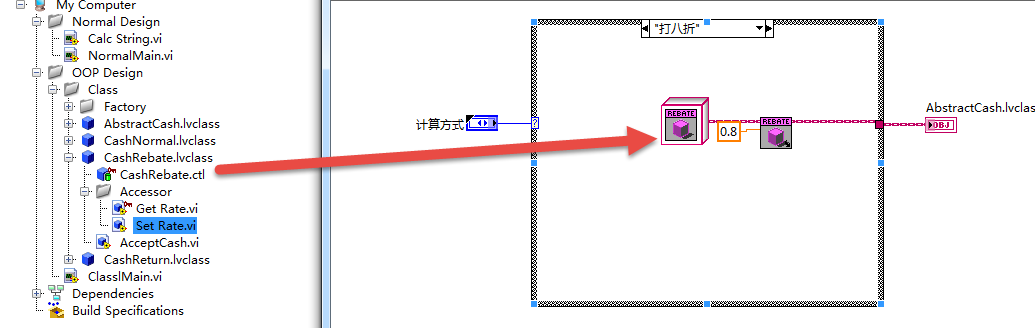
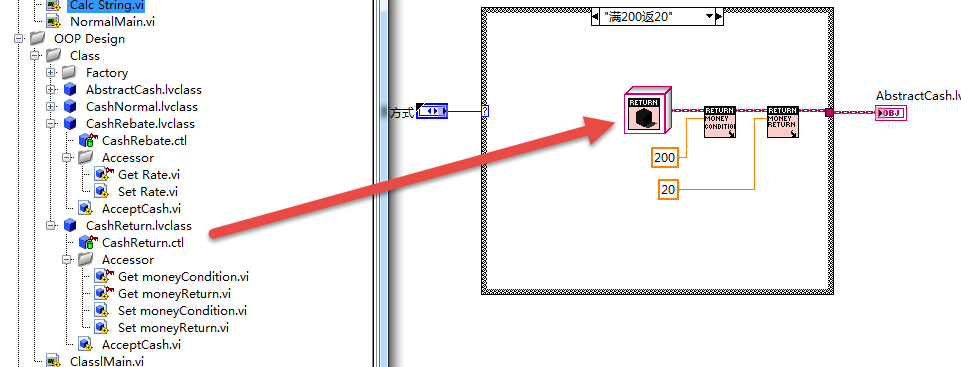
主程序设计
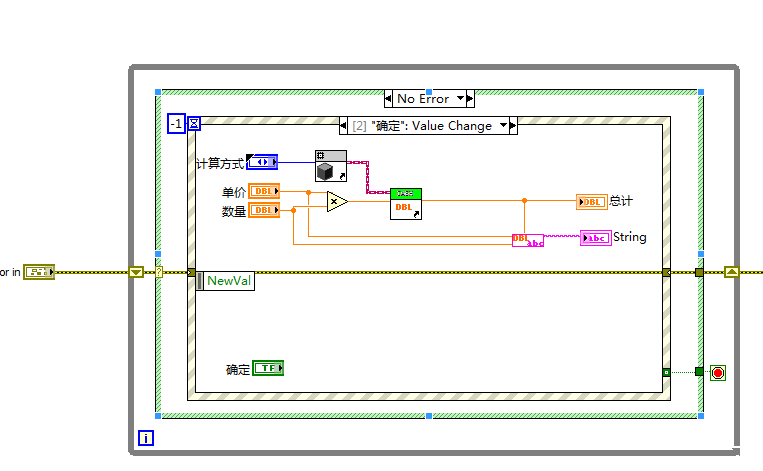
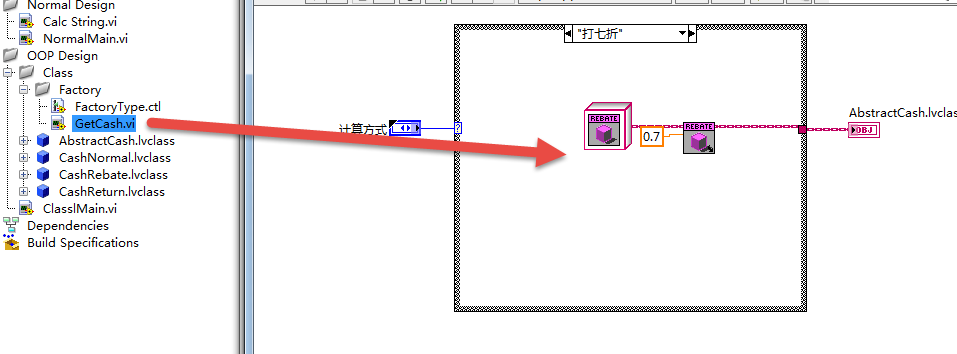
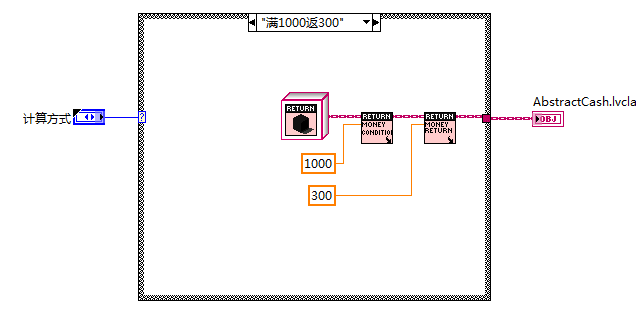
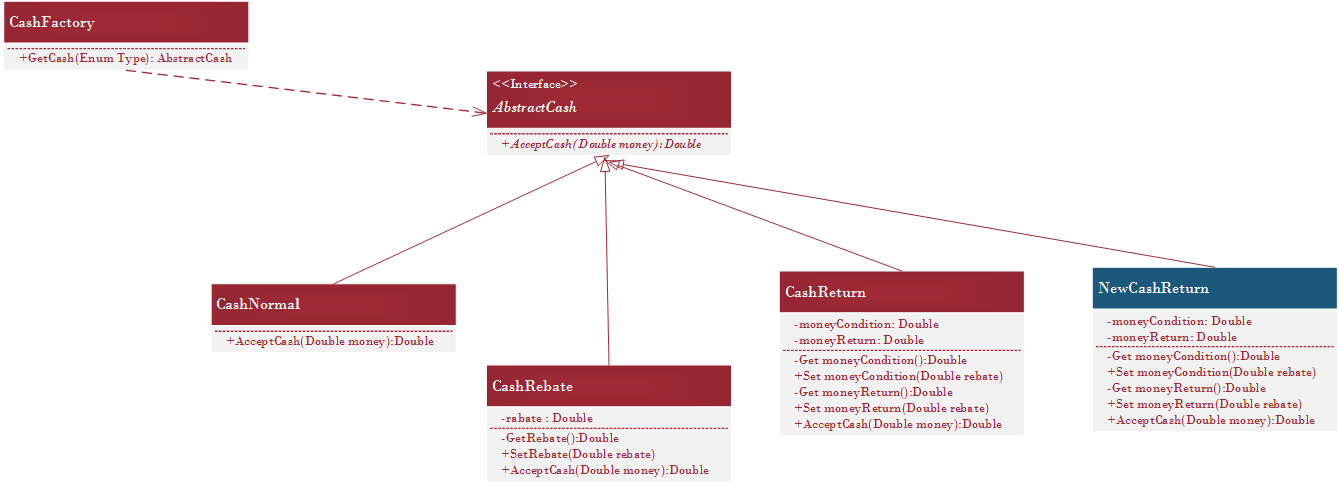
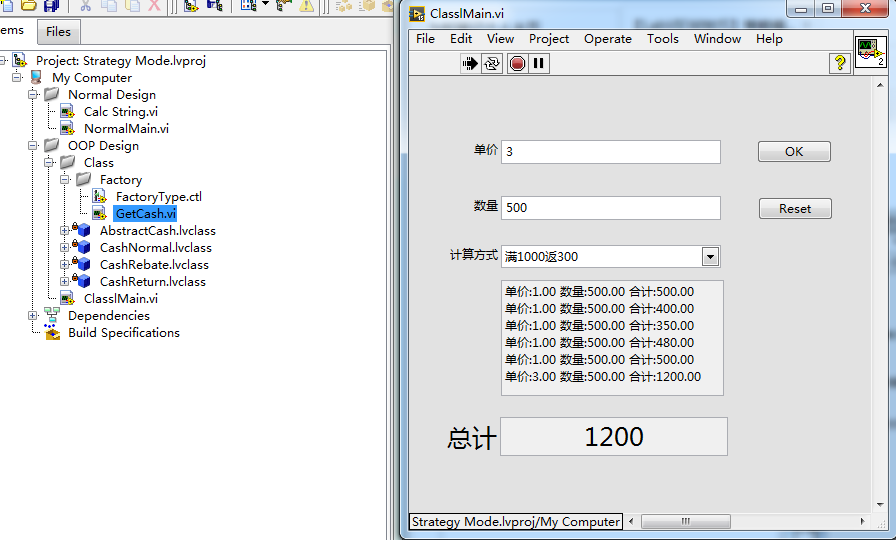
策略模式实现
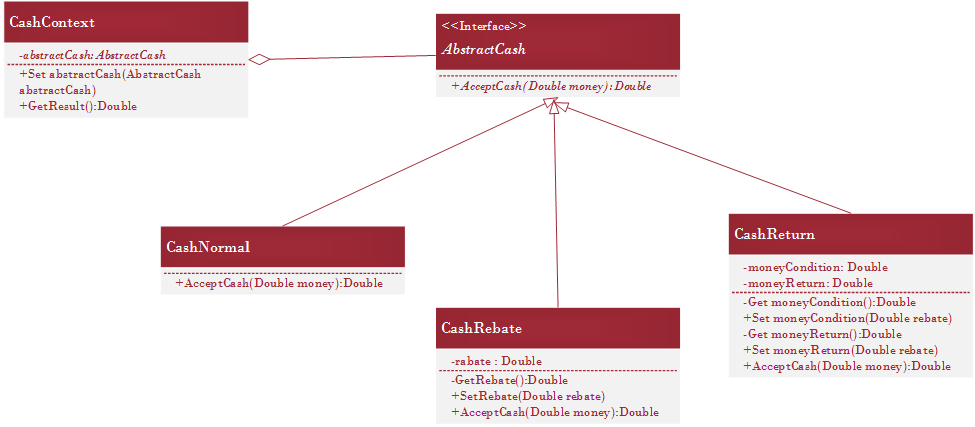
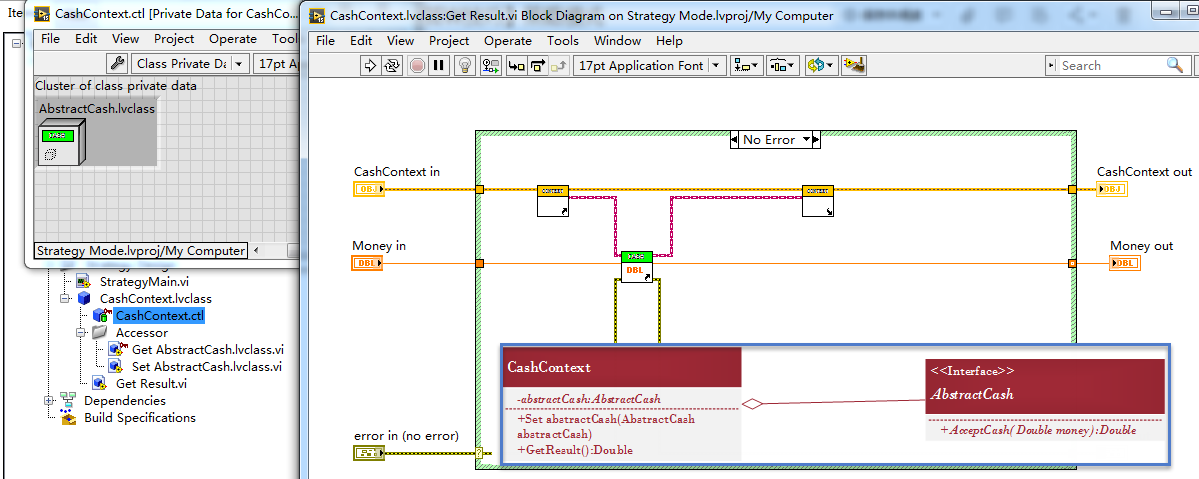
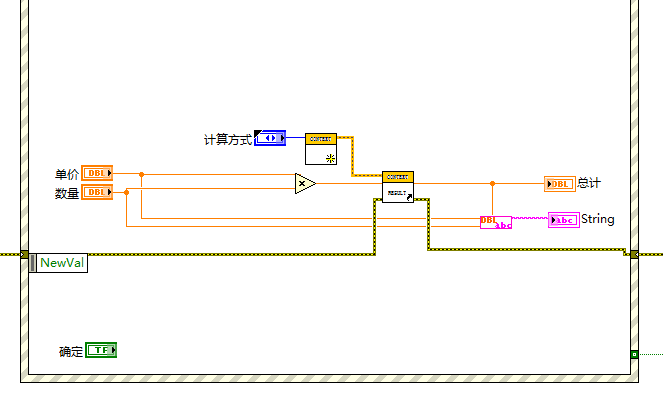
使用策略模式封装后发现,相比于简单工厂模式的例子,
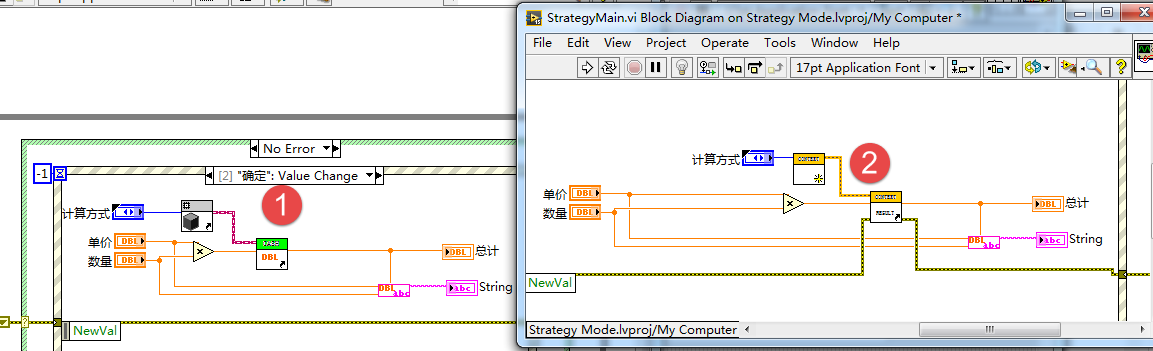
继续优化代码
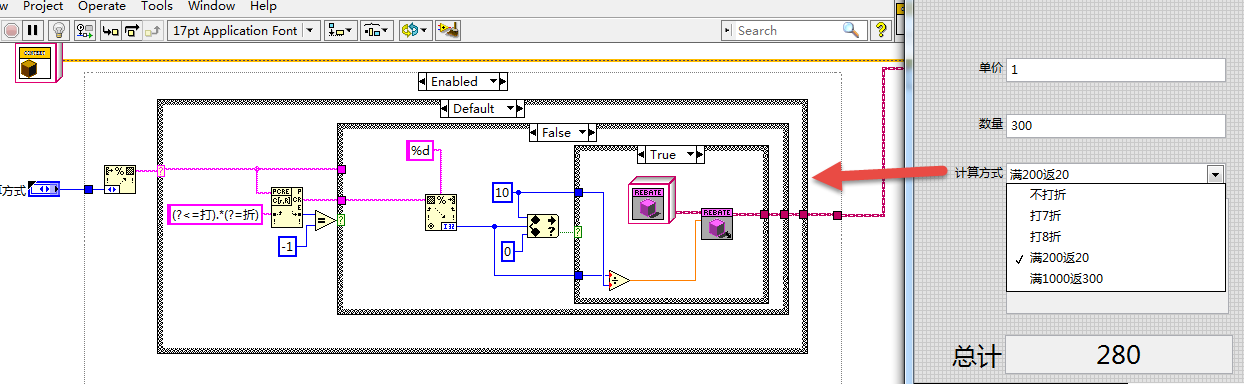
总结
后记

【LabVIEW技巧】策略模式的更多相关文章
- 【LabVIEW技巧】工厂模式_简单工厂
前言 上一个文章介绍了如何学习LabVIEW OOP,简要的提及了一些OOP学习中注意的事项,许多文章的读者反映写的太范,后文会逐步缩小范围,讨论在LabVIEW中各个模式的应用. 工厂模式概述 工厂 ...
- 大熊君说说JS与设计模式之------策略模式Strategy
一,总体概要 1,笔者浅谈 策略模式,又叫算法簇模式,就是定义了不同的算法,并且之间可以互相替换,此模式让算法的变化独立于使用算法的客户. 策略模式和工厂模式有一定的类似,策略模式相对简单容易理解,并 ...
- LVOOP设计模式在路上(二)-- 策略模式
前言 最近工作还挺忙的,连着好些周都是单休了,今天休息在家就来写写关于策略模式的理解和labivew的实现. 正文 1.什么是策略模式 定义是这样描述的:它定义了算法家族,分别封装起来,让它们之间可以 ...
- 设计模式 (一)——策略模式(Strategy,行为型)
1.概述 使用设计模式可以提高代码的可复用性.可扩充性和可维护性.策略模式(Strategy Pattern)属于行为型模式,其做法是将类所需的行为或者算法一个个封装成单独的类,并将其作为类的数据成员 ...
- 【LabVIEW技巧】LabVIEW OOP怎么学
前言 有很多人对LabVIEW OOP存在比较极端的看法,大致分为两类: 1. 绝对否定派认为LabVIEW OOP只不过是LabVIEW为了追求时髦,在面向过程的基础上用簇做了一些特性,实际上完全不 ...
- 《Mybatis 手撸专栏》第10章:使用策略模式,调用参数处理器
作者:小傅哥 博客:https://bugstack.cn 沉淀.分享.成长,让自己和他人都能有所收获! 一.前言 你这代码写的,咋这么轴呢! 说到轴,让我想起初中上学时老师说的话:"你那脑 ...
- javascript设计模式:策略模式
前言 策略模式有效利用组合.委托.多态等技术和思想,可以有效避免多重条件选择语句. 策略模式对开放-封闭原则提供了很好的支持,将算法封装在strategy中,使得他们易于切换.理解.扩展. 策略模式中 ...
- StrategyPattern (策略模式)
/** * 策略模式 * @author TMAC-J * 根据环境的不同选择不同的策略,把策略用接口抽象出来 */ public class StrategyPattern { interface ...
- JAVA 设计模式之策略模式
定义:定义一组算法,将每个算法都封装起来,并且使他们之间可以互换. 类型:行为类模式 策略模式是对算法的封装,把一系列的算法分别封装到对应的类中,并且这些类实现相同的接口,相互之间可以替换.在前面说过 ...
随机推荐
- Socket网络编程实例2
两个程序通过“网络”交互数据就使用socket,它只负责两件事:建立连接,传递数据. 所有的数据传输接收,必须都使用byte格式 1.简单实例: #客户端 import socket client=s ...
- Git的安装与使用(一)
闲来无事写了个小demo,想上传到GitHub上,发现得使用git进行上传,所以得先了解下git . 1.git是什么 分布式版本控制器 2.svn与git的区别 svn:是集中式的版本控制系统,版本 ...
- 【以前的空间】bzoj [ZJOI2007]棋盘制作
具体可以去跪<浅谈用极大化思想解决最大子矩形问题>(p.s. 蒟蒻跪了还是很晕,不过想到之前usaco好像是最后一章的一道题……看了下代码顿然醒悟) 也就是如果用o(nm)的方法维护一个极 ...
- BZOJ4890 & 洛谷3761:[TJOI2017]城市——题解
https://www.lydsy.com/JudgeOnline/problem.php?id=4890 https://www.luogu.org/problemnew/show/P3761 从加 ...
- BZOJ3343 & 洛谷2801:教主的魔法——题解
http://www.lydsy.com/JudgeOnline/problem.php?id=3343 https://www.luogu.org/problemnew/show/2801 题目描述 ...
- BZOJ1597 土地购买 【dp + 斜率优化】
1597: [Usaco2008 Mar]土地购买 Time Limit: 10 Sec Memory Limit: 162 MB Submit: 5466 Solved: 2035 [Submi ...
- 洛谷 P4555 [国家集训队]最长双回文串 解题报告
P4555 [国家集训队]最长双回文串 题目描述 顺序和逆序读起来完全一样的串叫做回文串.比如acbca是回文串,而abc不是(abc的顺序为abc,逆序为cba,不相同). 输入长度为\(n\)的串 ...
- POJ.2739 Sum of Consecutive Prime Numbers(水)
POJ.2739 Sum of Consecutive Prime Numbers(水) 代码总览 #include <cstdio> #include <cstring> # ...
- 调整KVM虚拟机硬盘大小
KVM虚拟机的硬盘映像默认存放在“/var/lib/libvirt/images/”中,先查看你的硬盘映像格式是不是RAW格式: qemu-img info /var/lib/libvirt/imag ...
- 常州模拟赛d7t3 水管
分析:第一问还是很好做的,关键是怎么做第二问.我们可以每次删掉最小生成树上的一条边,然后再求一次最小生成树,看边权和大小和原来的是不是一样的,不过这个做法效率很低. 考虑Kruskal算法的原理,每次 ...
