LeetCode第[62]题(Java)：Unique Paths 及扩展

题目：唯一路径（机器人走方格）

难度：Medium

题目内容：

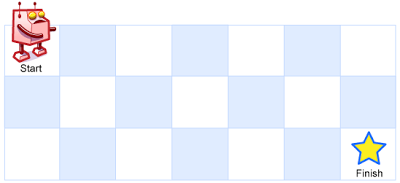
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

翻译：

机器人位于m x n网格的左上角（在下图中标记为“开始”）。

机器人只能在任何时间点移动或向右移动。机器人正试图到达网格的右下角（在下图中标记为“Finish”）。

有多少种可能的路径？

Note: m and n will be at most 100.

Example 1:

Input: m = 3, n = 2
Output: 3

Example 2:

Input: m = 7, n = 3
Output: 28

我的思路：动态规划题，每个点（m，n）都是由（m-1，n）+（m，n-1）这两个点的可能数之和。最简单的方法就是用递归来实现。

我的代码：

     public int uniquePaths(int m, int n) {
         if (m == 1 || n==1) {
             return 1;
         }
         return uniquePaths(m,n-1) + uniquePaths(m-1,n);
     }

我的复杂度：O（m*n）    空间复杂度也是O（m*n） ——递归深度

结果：41 / 62 test cases passed.     Time Limit Exceeded

Last executed input:   51  9

递归就是这样，代码很简单，但是运行速度很慢，稍微大一点就会超时。

答案代码：

     public int uniquePaths(int x, int y) {
         int dp[][] = new int[x][y];
         for(int i = 0; i< x;i++){
             for(int j = 0;j<y;j++){
                 if (i == 0 || j == 0) {
                     dp[i][j] = 1;
                     continue;
                 }
                 dp[i][j] = dp[i-1][j] + dp[i][j-1];
             }
         }
         return dp[x-1][y-1];
     }

答案复杂度：O（m*n）    空间复杂度也是O（m*n）  虽然复杂度都一样，但是由于用迭代替换了递归，运行速度大大提高。

答案思路：递归无非就是把本层的计算调用深一层的计算，然后将深一层的结果返回，所以如果将从第一层到最后一层所有的值都计算出来并由某种数据结构保存，那么就可以直接迭代进行计算。

所以一维的递归：一维只会与一维相关，所以一路直线迭代即可。例如：求阶乘（只与上一个有关，记录一个即可）、斐波那契数列（与上两个有关，需要记录两个）

　　二维的递归：每一个元素都与两个维度相关，所以得借用二维数组来记录所有值。

扩展：当x == y的时候，此时为正方格，是否有更好的方法？

　　因为此时类似于卡特兰数，此时有 f（n+1）=f（n）* （4*n-2），所以代码中加入方形判断可以优化方形的计算速度，如下：

        if (x == y) {
            int ans = 1;
            for (int i = 1; i < x; i++) {
                ans = ans * (4*i-2)/i;
            }
            return ans;
        } 

注意：当要使用  “  *=  ”  这种符号的时候，如果右边是一个表达式且含有 除号 ，那么最好还是不要使用，因为这个运算符是先运算右边再乘自己，所以有可能右边的计算顺序就不对了。

例如当x==y==4的时候  此时ans = =6   而  i ==3 ，如果使用  ans *= (4*i -2)/i; 所以先计算右边就有   10 /  3 = 3,  然后再乘以6  最后结果为18,结果错误。

而使用 ans = ans * (4*i-2)/i; 就不会有此错误。