SMU Autumn 2023 Round 1(Div.1)

SMU Autumn 2023 Round 1(Div.1)

A. Set or Decrease(枚举)

题意就是你可以进行两种操作,将\(a_i-1\)或者令\(a_i\)等于\(a_j\),然后使得\(\sum\limits_{i=1}^{n}a_i \leq k\),求最少的操作步数

首先我们让一个大数变成一个最小数的贡献肯定是要比让大数减一产生的贡献更多,所以我们可以排序后去枚举将后面\(i\)个数变成最小数后得到的和\(Sum\)来与\(k\)比较,求和可以用前面\((n-i-1)\)个数的前缀和加上后面\(i\)个最小数,即\(a_0\),如果这个和仍然大于\(k\),那我们就要执行减一操作了,因为后面的大数都等于最小数了,所以这个减一操作也是只有最小数减一才能贡献最大,至于要减多少,那就是\(\lceil \frac{Sum-k}{i} \rceil\),即将这个差值平均分到后面的\(i\)个数中,且\(Sum \leq k\),所以我们一定得向上取整,每次的步数即\(i+\lceil \frac{Sum-k}{i} \rceil\),然后取最小值即可

#include <bits/stdc++.h>
#define int long long
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;

void solve() {
	int n, k;
	cin >> n >> k;
	vector<int> a(n);
	for (auto &i : a)
		cin >> i;

	sort(a.begin(), a.end());
	vector<int> num(n);
	num[0] = a[0];
	for(int i = 1;i < n;i ++)
		num[i] = num[i - 1] + a[i];

	int ans = 1e15;
	for(int i = 0;i < n;i ++){
		int s = num[n - i - 1] + a[0] * i;
		int t = i;
		if(s > k){
			t += (s - k + i) / (i + 1);
		}
		ans = min(ans, t);
	}

	cout << ans << '\n';

}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}

	return 0;
}

E. Exact Change(暴力枚举)

题意就是用面值为\(1,2,3\)的三种纸币去凑出\(n\)个数,且要让使用的纸币数最少

首先肯定是尽量的去使用面值为\(3\)的纸币,面值为\(1\)的最多使用\(1\)张,再多就可以用纸币\(2\)或\(3\)代替,纸币\(2\)最多使用\(2\)张,\(3\)张纸币\(2\)可以用\(2\)张纸币\(3\)代替,数据范围较小,可以直接去暴力枚举使用纸币\(1\)和纸币\(2\)的数量,然后去找出当使用\(i\)张纸币\(1,j\)张纸币\(2\)时使得所有数能凑出的纸币\(3\)最大所需要的数量\((res)\),则总使用张数为\((res + i+j)\),然后在枚举\(i,j\)的过程中判断一下最小值就行了

#include <bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;
using i64 = long long;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		int n;
		cin >> n;
		vector<int> a(n);
		for (auto &i : a) cin >> i;

		i64 ans = INT_MAX;
		for (int i = 0; i <= 1; i ++) {
			for (int j = 0; j <= 2; j ++) {
				i64 res = 0;
				for (auto ai : a) {
					i64 v3 = INT_MAX;
					for (int x1 = 0; x1 <= i; x1 ++) {
						for (int x2 = 0; x2 <= j; x2 ++) {
							i64 ak = ai - x1 - 2 * x2;
							if (ak >= 0 && ak % 3 == 0)
								v3 = min(v3, ak / 3);
						}
					}
					res = max(res, v3);
				}
				ans = min(ans, res + i + j);
			}
		}

		cout << ans << '\n';

	}

	return 0;
}

F. Replace the Numbers(离线)

题意是给出两种操作,操作\(1\)是在序列后添加一个数,操作\(2\)是将序列中的\(x\)都替换成\(y\),问\(q\)次操作后的序列

可以发现的是,每一步操作\(2\)都会影响这一步之前的序列,如果暴力做的话就需要每次都循环一遍之前的序列,但如果我们反过来看,从最后一步往前的话,那么每一步操作\(2\)影响的就是之后的序列了,假设\(f_x \rightarrow x, f_y \rightarrow y\),遇到操作\(1\)的话,直接加上对应的值即可,遇到操作\(2\)的话,就要让\(f_x \rightarrow f_y\),而不能直接让\(f_x \rightarrow y\),因为\(y\)之后还可能已经变成其他值了,如\(f_y \rightarrow z\),那么这一步应该是\(f_x \rightarrow f_y \rightarrow z\),之后又遇到操作\(1\),直接加上\(f_x \rightarrow \dots \rightarrow z\)即可,因为是从后往前操作的,所以最后输出要倒序输出

#include <bits/stdc++.h>
#define debug(a) cout<<#a<<"="<<a<<'\n';

using namespace std;
using i64 = long long;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int q;
	cin >> q;
	vector<int> f(500005),opt(q + 1),x(q + 1),y(q + 1);
	iota(f.begin(), f.end(),0);

	for(int i = 1;i <= q;i ++){
		cin >> opt[i];
		if(opt[i] == 1)
			cin >> x[i];
		else
			cin >> x[i] >> y[i];
	}

	vector<int> ans(q + 1);
	int l = 0;
	for(int i = q;i >= 1;i --){
		if(opt[i] == 1)
			ans[++l] = f[x[i]];
		else
			f[x[i]] = f[y[i]];
	}

	for(int i = l;i >= 1;i --)
		cout << ans[i] << ' ';

	return 0;
}

G. Triangles on a Rectangle

题意是给你一个矩形,然后四条边每条边至少有两个点,然后在这个矩形中选三个点使得组成的三角形面积最大

画个图其实就能看出了

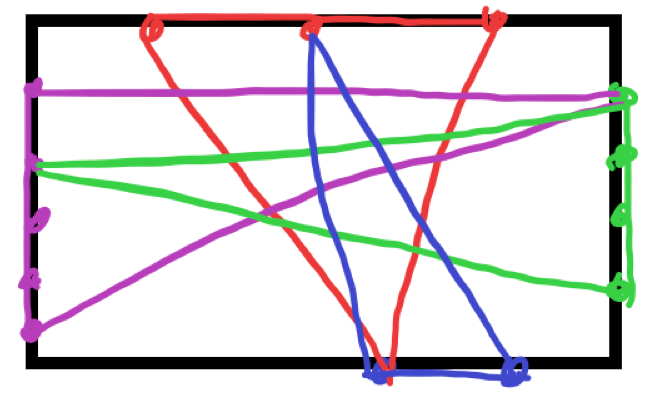
就是找每条边上最远的两点和长或宽作为高组成的三角形最大的即可

#include <bits/stdc++.h>
#define int long long

using namespace std;

void solve() {
	int w, h;
	cin >> w >> h;
	int ans = 0;
	int k, x;
	cin >> k;
	int ma = 0, mi = 1e7;
	for (int i = 0; i < k; i ++) {
		cin >> x;
		mi = min(x, mi);
		ma = max(ma, x);
	}
	ans = (ma - mi) * h;
	cin >> k;
	ma = 0, mi = 1e7;
	for (int i = 0; i < k; i ++) {
		cin >> x;
		mi = min(x, mi);
		ma = max(ma, x);
	}
	ans = max(ans, (ma - mi) * h);
	cin >> k;
	ma = 0, mi = 1e7;
	for (int i = 0; i < k; i ++) {
		cin >> x;
		mi = min(x, mi);
		ma = max(ma, x);
	}
	ans = max(ans, (ma - mi) * w);
	cin >> k;
	ma = 0, mi = 1e7;
	for (int i = 0; i < k; i ++) {
		cin >> x;
		mi = min(x, mi);
		ma = max(ma, x);
	}
	ans = max(ans, (ma - mi) * w);
	cout << ans << '\n';
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);

	int T;
	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}