Linux字节对齐的那些事

最近一口君在做一个项目，遇到一个问题，ARM上的threadx在与DSP通信采用消息队列的方式传递消息（最终实现原理是中断+共享内存的方式），在实际操作过程中发现threadx总是crash，于是经过排查，是因为传递消息的结构体没有考虑字节对齐的问题。

随手整理一下C语言中字节对齐的问题与大家一起分享。

一、概念

对齐跟数据在内存中的位置有关。如果一个变量的内存地址正好位于它长度的整数倍，他就被称做自然对齐。比如在32位cpu下，假设一个整型变量的地址为0x00000004，那它就是自然对齐的。

首先了解什么位、字节、字

名称	英文名	含义
位	bit	1个二进制位称为1个bit
字节	Byte	8个二进制位称为1个Byte
字	word	电脑用来一次性处理事务的一个固定长度

字长

一个字的位数，现代电脑的字长通常为16，32， 64位。(一般N位系统的字长是N/8字节。)

不同的CPU一次可以处理的数据位数是不同的，32位CPU可以一次处理32位数据，64位CPU可以一次处理64位数据，这里的位，指的就是字长。

而所谓的字长，我们有时会称为字（word）。在16位的CPU中，一个字刚好为两个字节，而32位CPU中，一个字是四个字节。若以字为单位，向上还有双字（两个字），四字（四个字）。

二、对齐规则

对于标准数据类型，它的地址只要是它的长度的整数倍就行了，而非标准数据类型按下面的原则对齐：

　　

数组 ：按照基本数据类型对齐，第一个对齐了后面的自然也就对齐了。

联合 ：按其包含的长度最大的数据类型对齐。

结构体： 结构体中每个数据类型都要对齐。

三、如何限制定字节对齐位数？

1. 缺省

在缺省情况下，C编译器为每一个变量或是数据单元按其自然对界条件分配空间。

一般地，可以通过下面的方法来改变缺省的对界条件：

2. #pragma pack(n)

· 使用伪指令#pragma pack (n)，C编译器将按照n个字节对齐。

· 使用伪指令#pragma pack ()，取消自定义字节对齐方式。

pragma pack(n) 用来设定变量以n字节对齐方式。

n字节对齐就是说变量存放的起始地址的偏移量有两种情况：

1. 如果n大于等于该变量所占用的字节数，那么偏移量必须满足默认的对齐方式
2. 如果n小于该变量的类型所占用的字节数，那么偏移量为n的倍数，不用满足默认的对齐方式。

结构的总大小也有一个约束条件，如果n大于等于所有成员变量类型所占用的字节数，那么结构的总大小必须为占用空间最大的变量占用的空间数的倍数；否则必须是n的倍数。

3. __attribute

另外，还有如下的一种方式：

· __attribute((aligned (n)))，让所作用的结构成员对齐在n字节自然边界上。如果结构中有成员的长度大于n，则按照最大成员的长度来对齐。

· attribute ((packed))，取消结构在编译过程中的优化对齐，按照实际占用字节数进行对齐。

3. 汇编.align

汇编代码通常用.align来制定字节对齐的位数。

.align:用来指定数据的对齐方式,格式如下：

.align [absexpr1, absexpr2]

以某种对齐方式,在未使用的存储区域填充值. 第一个值表示对齐方式,4, 8,16或 32. 第二个表达式值表示填充的值。

四、为什么要对齐？

操作系统并非一个字节一个字节访问内存，而是按2，4，8这样的字长来访问。

因此，当CPU从存储器读数据到寄存器，IO的数据长度通常是字长。

如32位系统访问粒度是4字节(bytes), 64位系统的是8字节。

当被访问的数据长度为n字节且该数据地址为n字节对齐时，那么操作系统就可以高效地一次定位到数据，

无需多次读取，处理对齐运算等额外操作。

数据结构应该尽可能地在自然边界上对齐。如果访问未对齐的内存，CPU需要做两次内存访问。

字节对齐可能带来的隐患:

代码中关于对齐的隐患，很多是隐式的。比如在强制类型转换的时候。例如：

unsigned int i = 0x12345678;
unsigned char *p=NULL;
unsigned short *p1=NULL;

p=&i;
*p=0x00;
p1=(unsigned short *)(p+1);
*p1=0x0000;

最后两句代码，从奇数边界去访问unsignedshort型变量，显然不符合对齐的规定。

在x86上，类似的操作只会影响效率，但是在MIPS或者sparc上，可能就是一个error,因为它们要求必须字节对齐.

五、举例

例1：os基本数据类型占用的字节数

首先查看操作系统的位数



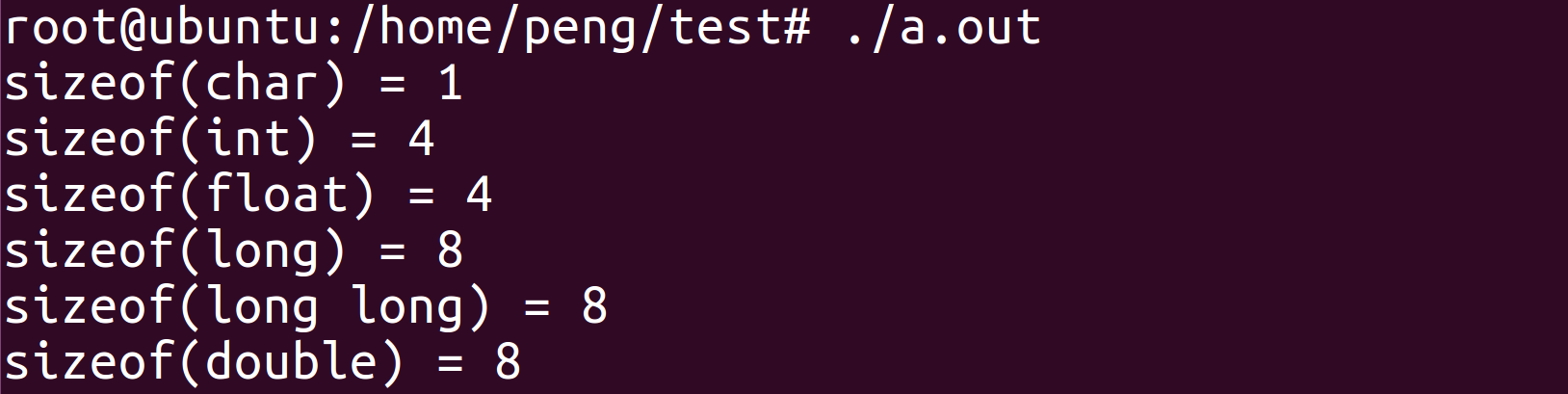
在64位操作系统下查看基本数据类型占用的字节数：

#include <stdio.h>

int main()
{
    printf("sizeof(char) = %ld\n", sizeof(char));
    printf("sizeof(int) = %ld\n", sizeof(int));
    printf("sizeof(float) = %ld\n", sizeof(float));
    printf("sizeof(long) = %ld\n", sizeof(long));
    printf("sizeof(long long) = %ld\n", sizeof(long long));
    printf("sizeof(double) = %ld\n", sizeof(double));
    return 0;
}

例2：结构体占用的内存大小--默认规则

考虑下面的结构体占用的位数

struct yikou_s
{
    double d;
    char c;
    int i;
} yikou_t;

执行结果

sizeof(yikou_t) = 16

在内容中各变量位置关系如下：

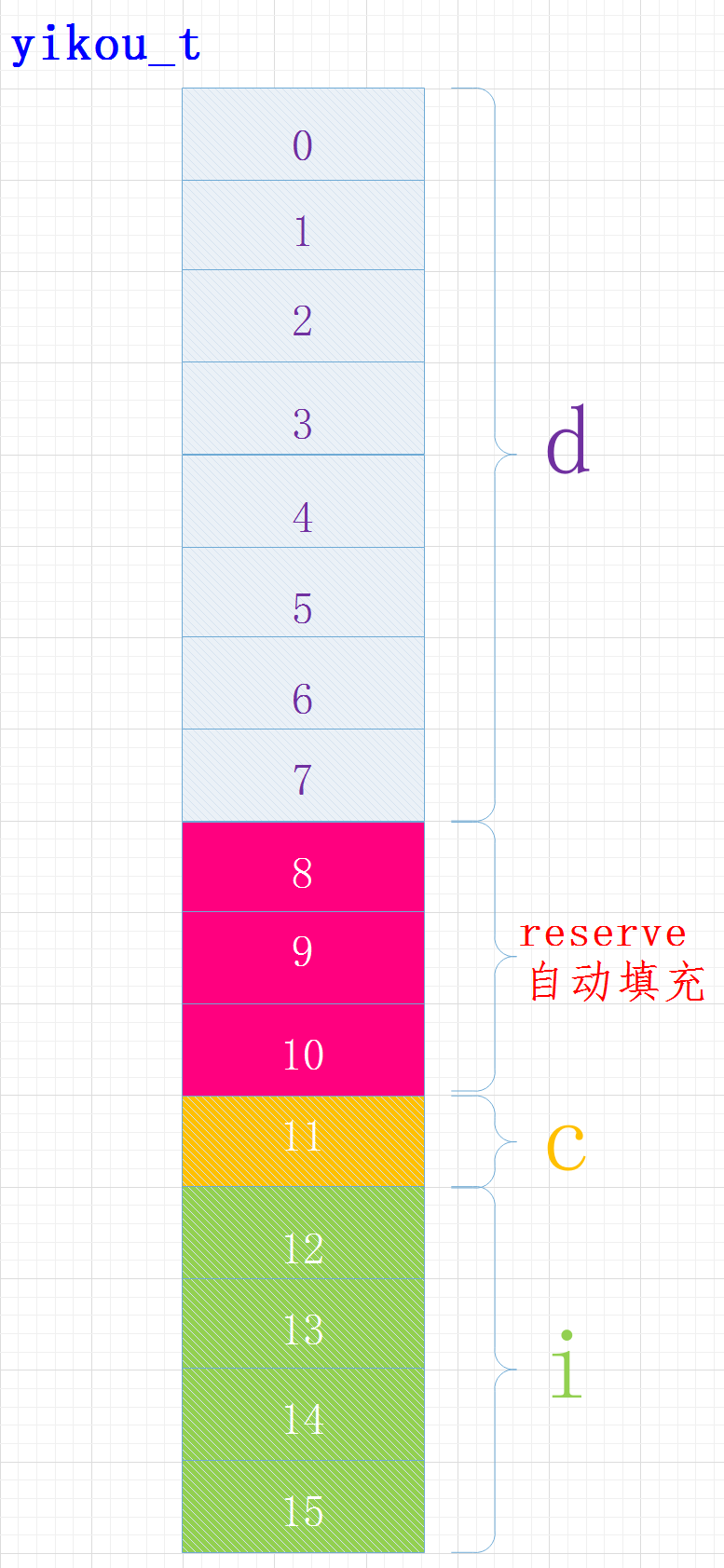
其中成员C的位置还受字节序的影响，有的可能在位置8

编译器给我们进行了内存对齐，各成员变量存放的起始地址相对于结构的起始地址的偏移量必须为该变量类型所占用的字节数的倍数, 且结构的大小为该结构中占用最大空间的类型所占用的字节数的倍数。

对于偏移量：变量type n起始地址相对于结构体起始地址的偏移量必须为sizeof(type(n))的倍数

结构体大小：必须为成员最大类型字节的倍数

char: 偏移量必须为sizeof(char) 即1的倍数
int: 偏移量必须为sizeof(int) 即4的倍数
float: 偏移量必须为sizeof(float) 即4的倍数
double: 偏移量必须为sizeof(double) 即8的倍数

例3：调整结构体大小

我们将结构体中变量的位置做以下调整：

struct yikou_s
{
    char c;
    double d;
    int i;
} yikou_t;

执行结果

sizeof(yikou_t) = 24

各变量在内存中布局如下：

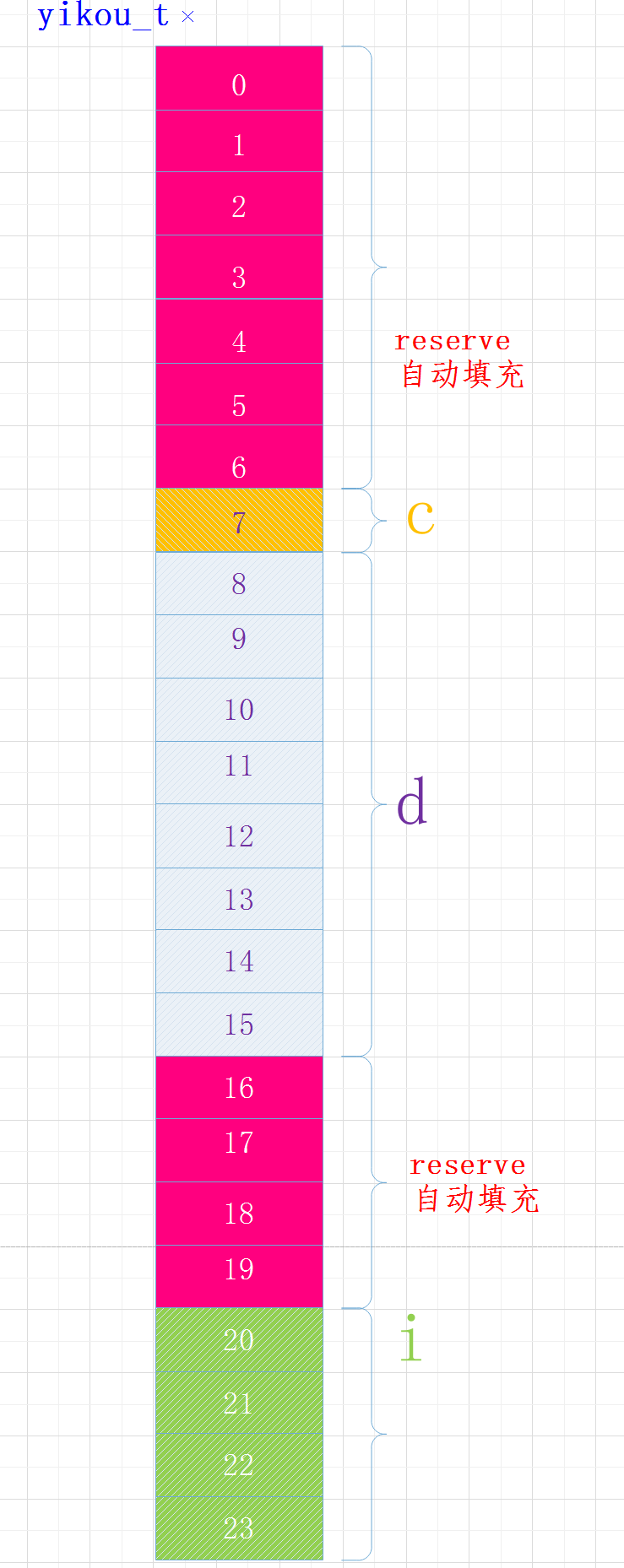
当结构体中有嵌套符合成员时，复合成员相对于结构体首地址偏移量是复合成员最宽基本类型大小的整数倍。

例4： #pragma pack(4)

#pragma pack(4)

struct yikou_s
{
    char c;
    double d;
    int i;
} yikou_t;

sizeof(yikou_t) = 16

例5：#pragma pack(8)

#pragma pack(8)

struct yikou_s
{
    char c;
    double d;
    int i;
} yikou_t;

sizeof(yikou_t) = 24

例6：汇编代码

举例：

以下是截取的uboot代码中异常向量irq、fiq的入口位置代码：

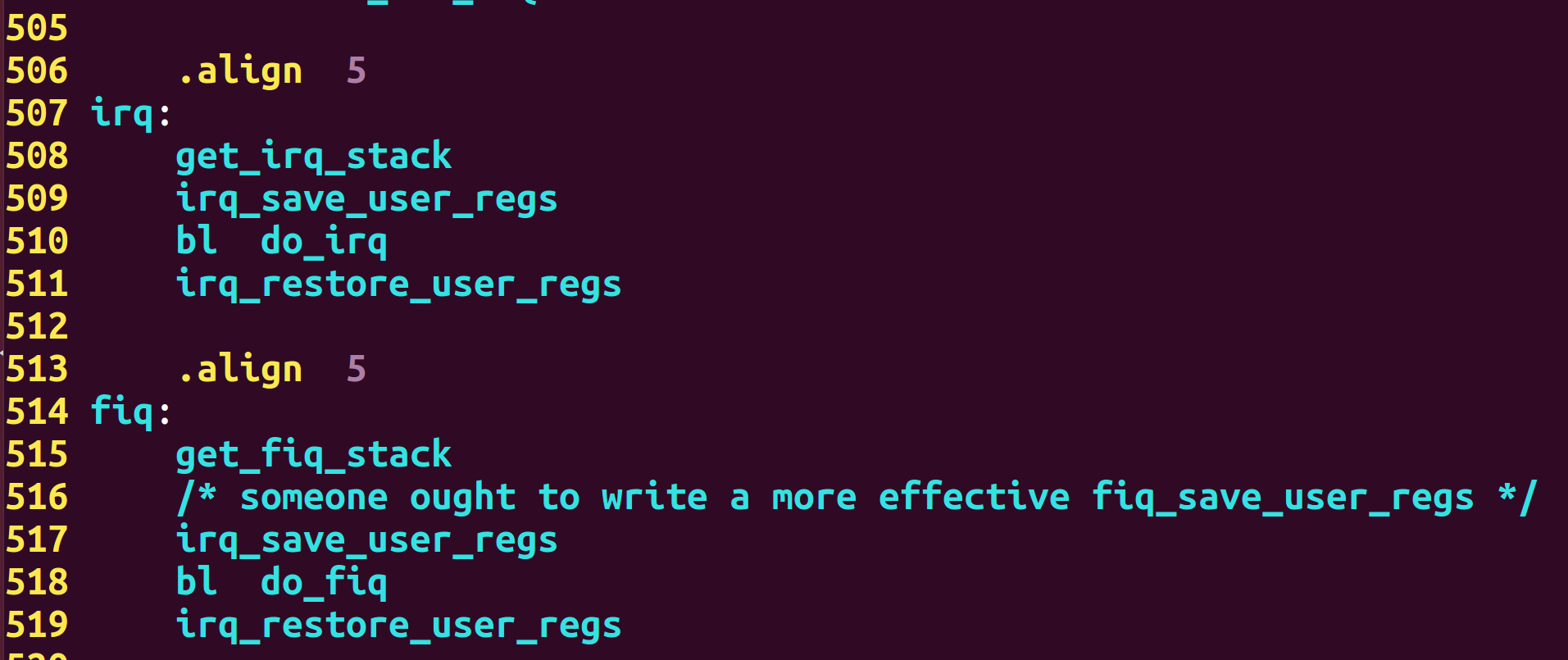
六、汇总实力

有手懒的同学，直接贴一个完整的例子给你们：

#include <stdio.h>
main()
{
struct A {
    int a;
    char b;
    short c;
};

struct B {
    char b;
    int a;
    short c;
};
struct AA {
   // int a;
    char b;
    short c;
};

struct BB {
    char b;
   // int a;
    short c;
};
#pragma pack (2) /*指定按2字节对齐*/
struct C {
    char b;
    int a;
    short c;
};
#pragma pack () /*取消指定对齐，恢复缺省对齐*/

#pragma pack (1) /*指定按1字节对齐*/
struct D {
    char b;
    int a;
    short c;
};
#pragma pack ()/*取消指定对齐，恢复缺省对齐*/

int s1=sizeof(struct A);
int s2=sizeof(struct AA);
int s3=sizeof(struct B);
int s4=sizeof(struct BB);
int s5=sizeof(struct C);
int s6=sizeof(struct D);
printf("%d\n",s1);
printf("%d\n",s2);
printf("%d\n",s3);
printf("%d\n",s4);
printf("%d\n",s5);
printf("%d\n",s6);
}