ACM算法竞赛代码模板（长期更新）

C++算法模板

基础算法

排序

快速排序

void quickSort(int q[], int l, int r) {
    if (l >= r) return;
    int i = l - 1, j = r + 1, x = q[l + r >> 1];
    while (i < j)
    {
        do i ++ ; while (q[i] < x);
        do j -- ; while (q[j] > x);
        if (i < j) swap(q[i], q[j]);
    }
    quickSort(q, l, j), quickSort(q, j + 1, r);
}

归并排序

void mergeSort(int q[], int l, int r) {
    if (l >= r) return;
    int mid = l + r >> 1;
    mergeSort(q, l, mid);
    mergeSort(q, mid + 1, r);
    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else tmp[k ++ ] = q[j ++ ];
    while (i <= mid) tmp[k ++ ] = q[i ++ ];
    while (j <= r) tmp[k ++ ] = q[j ++ ];
    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

二分

整数二分

bool check(int x) {/* ... */} // 检查x是否满足某种性质

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bSearch_1(int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bSearch_2(int l, int r) {
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

浮点数二分

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bSearch_3(double l, double r) {
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps) {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

高精度

高精度加法

// C = A + B, A >= 0, B >= 0
vector<int> add(vector<int> &A, vector<int> &B) {
    if (A.size() < B.size()) return add(B, A);
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size(); i ++ ) {
        t += A[i];
        if (i < B.size()) t += B[i];
        C.push_back(t % 10);
        t /= 10;
    }
    if (t) C.push_back(t);
    return C;
}

高精度减法

// C = A - B, 满足A >= B, A >= 0, B >= 0
vector<int> sub(vector<int> &A, vector<int> &B) {
    vector<int> C;
    for (int i = 0, t = 0; i < A.size(); i ++ ) {
        t = A[i] - t;
        if (i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if (t < 0) t = 1;
        else t = 0;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

高精度乘低精度

// C = A * b, A >= 0, b >= 0
vector<int> mul(vector<int> &A, int b) {
    vector<int> C;
    int t = 0;
    for (int i = 0; i < A.size() || t; i ++ ) {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

高精度除以低精度

// A / b = C ... r, A >= 0, b > 0
vector<int> div(vector<int> &A, int b, int &r) {
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- ) {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

离散化

vector<int> alls; //存储所有待离散化的值
sort(alls.begin(), alls.end()); //将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); //去掉重复元素

//二分求出x对应的离散化的值
int find(int x) {
    int l = 0, r = alls.size() - 1;
    while(l < r) {
        int mid = l + r >> 1;
        if(alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

尺取法（双指针）

for (int i = 0, j = 0; i < n; i ++ ) {
    while (j < i && check(i, j)) j ++ ;
    // 具体问题的逻辑
}
//常见问题分类：
    //(1) 对于一个序列，用两个指针维护一段区间
    //(2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

数论与数学知识

c++求上取整

\(\lceil \frac{l}{p} \rceil = \lfloor \frac{l+p-1}{p} \rfloor\)

快速幂

int qpow(int a, int b, int c){
	int res = 1;
    while(b){
        if(b & 1) res = res * a % c; //不可写成res *= a % c
        b >>= 1;
        a = a * a % c;
    }
    return res;
}

逆元

费马小定理求逆元

费马小定理(Fermat's little theorem)是数论中的一个重要定理，在1636年提出。如果p是一个质数，而整数a不是p的倍数，则有

\(a^{p-1} \equiv 1 (mod \ p)\)

对上式变形得

\(a^{p-2}a\equiv1(mod \ p)\)

则a mod p的逆元是\(a^{p-2}\)

接下来通过qpow(a, p - 2, p)即可求出a mod p的逆元

快速幂求逆元

基于费马小定理，求\(a \ mod \ p\)的逆元。

要求是p是一个质数，并且p与a互质。

int qPow(int a, int b, int k) {
    int ans = 1;
    while (b) {
        if (b & 1) ans = (LL)ans * a % k;
        a = (LL)a * a % k;
        b >>= 1;
    }
    return ans;
}

{
    int res = q_pow(a, p - 2, p);
    if (a % p) printf("%d\n", res);
    else puts("impossible");
}

线性逆元

证明：

线性求解n个数字的逆元，需要找到新元素的逆元同以往求解过逆元的关系。

以下面式子举例,对于要求解逆元的k,模数为p，有：

$ p=ak + b \ (b < a,k)$

进而有：

\(ak + b \equiv 0\, (mod\,p)\)

两边同时乘以k-1b-1,得到：

\(ab^{-1} + k^{-1} \equiv 0\,(mod\,p) \\\)

即

\(k^{-1}\equiv-ab^{-1}\,(mod\,p)\)

我们知道，

\(a=\left \lfloor p \over k\right \rfloor \\\)

\(b=p\,mod\,k\)

因此，有

\(k^{-1}\equiv - \left \lfloor p\over k\right \rfloor(p\,mod\,k)^{-1}\)

inv[1] = 1;

for (int i = 2; i <= n; i++) {
    inv[i] = (p - p / i) * inv[p % i] % p;
}

求解n个不同数字的逆元

求解n个不同数字的逆元，可以先维护一个前缀积，其最后一项是所有数字的乘积，求该项的逆元即求所有项逆元的乘积。由于逆元的特殊性质，逆元的乘积乘上其中某个元素即会消去对应的元素，因此我们可以借助前缀积来逐个迭代处理出所有数字的逆元。

\((∏\limits^n\limits_{i=1}a_i)^{−1}≡∏\limits^n\limits_{i=1}a_i^{-1}(mod\ p)\)

或

\((a_1a_2...a_n)^{-1}\equiv a_1^{-1}a_2^{-1}...a_n^{-1}(mod\ p)\)

且有

\(∏\limits_{i=1}\limits^na^{−1}_i∗a_n≡∏\limits^{n-1}_{i=1}a_i^{-1}\)

于是便可以处理处所有元素的逆元：

/*s是前缀积，inv是逆元*/
s[1] = a[1];
/*计算前缀积*/
for(int i = 2;i <= n;i++){
	s[i] = s[i - 1] * a[i] % p;
}
/*处理所有元素乘积的逆元，使用快速幂发求解单个逆元*/
inv[n] = fpow(s[n],p - 2);
/*逆元的前缀积*/
for(int i = n - 1;i >= 1;i--){
	inv[i] = inv[i + 1] * a[i + 1] % p;
}
/*计算全部逆元*/
for(int i = 2;i <= n;i++){
	inv[i] = inv[i] * s[i - 1] % p;
}
————————————————
版权声明：本文为CSDN博主「卷儿~」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/wayne_lee_lwc/article/details/107870741

扩展欧几里得算法

int exgcd(int a, int b, int &x, int &y)  // 扩展欧几里得算法, 求x, y，使得ax + by = gcd(a, b)
{
    if (!b)
    {
        x = 1; y = 0;
        return a;
    }
    //d始终都是a和b的最大公约数, 倒着传参是为了简化计算
    int d = exgcd(b, a % b, y, x);
    y -= (a / b) * x;
    return d;
    //返回d，使得能够在求最大公约数的同时完成x，y的凑整
}

高斯消元法

int gauss() {
    int c, r;
    for (r = 1, c = 1; c <= n; c ++) {
        int t = r;
        for (int i = r + 1; i <= n; i ++)
            if (fabs(a[i][c]) - fabs(a[t][c]) > eps) t = i;
        if (fabs(a[t][c]) < eps) continue;
        if (t != r) swap(a[t], a[r]);
        for (int i = n + 1; i >= c; i --) a[r][i] /= a[r][c];
        for (int i = r + 1; i <= n; i ++) {
            if (fabs(a[i][c]) > eps)
                for (int j = n + 1; j >= c; j --)
                    a[i][j] -= a[r][j] * a[i][c];
        }
        r ++;
    }
    if (r <= n) {
        for (int i = r; i <= n; i ++) {
            if (fabs(a[i][n + 1]) > eps) return 2; // 代表有无穷多组解
        }
        return 1; // 代表无解
    }
    for (int i = n; i >= 1; i --) {
        for (int j = i + 1; j <= n; j ++) {
            a[i][n + 1] -= a[i][j] * a[j][n + 1];
        }
    } // 代表有唯一组解
    return 0;
}

筛质数

朴素筛法

void getPrimes(int n) {
    for (int i = 2; i <= n; i ++) {
        if (!st[i]) {
            primes[cnt ++] = n;
        }
        for (int j = i + i; i <= n; j += i) st[j] = true;
    }
}

时间复杂度分析：

每个数的倍数都被筛掉了，因此时间复杂度为：

\(\frac{n}{2}+\frac{n}{3}+\dots+\frac{n}{n}\)

\(=n(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{n})\)

\(=n(ln(n)+c)\) 其中c是一个欧拉常数，是一个无限不循环小数，值是0.577左右

质数定理

1~n中有\(\frac{n}{ln(n)}\)个质数

我们可以只用把质数的倍数删掉，这样粗劣的时间复杂度就是\(\frac{n(ln(n))}{ln(n)}\)，但是这只是个粗略的估计，这个估计是不对的，真实的时间复杂度是\(O(nlog(log(n)))\)。

这个算法也就是下面的埃氏筛法。

埃氏筛法

//O(nloglogn)
int getPrimes(int n){
    int idx = 1;
    for(int i = 2; i <= n; i ++){
        if(!st[i]){
            prime[idx++] = i;
            for(int j = i + i; j <= n; j += i) st[j] = 1;
        }
    }
    return idx - 1;
}

线性筛法

线性筛法在10⁷次方的情况下会比埃氏筛法快一倍左右，在10⁶的情况下两个算法速度差不多。

整体思路：n只会被它的最小质因子筛掉

void getPrimes(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]) primes[cnt++] = i;
        // primes[j] <= n / i即primes * i <= n，即x <= n
        for(int j = 0; primes[j] <= n / i; j++){
            // 当还没有执行到下面的break语句时
            // 由于我们是从小到大枚举所有质数的，且还没有枚举到i的最小质因子
            // 所以当前的primes[j]一定是primes[j] * i的最小质因子
            // 所以就把primes[j] * i筛掉
            st[primes[j] * i] = true;
            // 当这段代码执行的时候就意味着primes[j]一定是i的最小质因子
            // primes[j]是从小到大枚举的质数，当第一次满足i % primes[j] == 0的时候
            // 说明primes[j]就一定是i的最小质因子
            // 同时此时primes[j]也一定是primes[j] * i的最小质因子
            // 因此上面的筛成立
            // 当如果此时再继续向后枚举质数，接下来的质数就不是primes[j] * i的最小质因子了
            // 因此要即时break掉
            if(i % primes[j] == 0) break;
        }
    }
}

证明线性：

对于一个合数x，假设primes[j]是x的最小质因子，当i枚举到x/primes[j]的时候，我们就可以在4到18行把x给筛掉。

第五行的判断条件不需要加j <= cnt

因为当i是合数的时候，primes[j]一定会在枚举到i的最小质因子时停下来，而i的最小质因子一定是小于i的，会在i之前被标记为primes，放到primes数组中来。

当i是质数的时候，当primes[j]=i的时候，枚举也会停下来。（是在break的时候停下来）

欧拉函数

\(\phi(n)\): 1~n中和n互质的数的个数

\(\phi(6)=2\)

一个数可以写成很多个质数的乘积的形式：

\(N=P_1^{\alpha_1}P_2^{\alpha_2}...P_k^{\alpha_k}\)

\(\phi(N)=N(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{{p_k}})\)

上式的证明会用到容斥原理。

那么如何计算从1~N中和N互质的数的个数呢

• 从1~N中去掉p1，p2，…，pk的所有倍数

  这里面就会多去一部分数，比如一个数可能既是p1的倍数又是p2的倍数

• 加上所有pi*pj的倍数

  \(N-\frac N {P_1} - \frac {N}{P_1} - ... - \frac N {P_1} + \frac N {P_1P_2} + \frac N {P_1 P_3} + ...\)

• 减去所有三个质数的倍数

  …

然后把最上面的式子展开，会发现这两个式子是相等的。

时间复杂度：时间复杂度瓶颈在分解质因数上，分解质因数的时间复杂度是\(O(\sqrt N)\)

代码：

int euler(int a) {
    int res = a;
    for (int i = 2; i <= a / i; i ++) {
        if (a % i == 0) {
            res = res / i * (i - 1);
            while (a % i == 0) a /= i;
        }
    }
    if (a > 1) res = res / a * (a - 1);
    return res;
}

筛法求欧拉函数

\(φ(ab)= \frac {φ(a)φ(b)gcd(a,b)} {φ(gcd(a,b))}\)

int getEuler(int n){
    phi[1] = 1;
    for(int i = 2; i <= n; i ++){
        if(!st[i]){
            prime[cnt ++] = i;
            phi[i] = i - 1;
        }
        for(int j = 0; prime[j] <= n / i; j ++){
            st[prime[j] * i] = true;
            if(i % prime[j] == 0){
                // 此时pj是i的最小质因子，i的质因子中有j了，所以pj*i的所有(1-pj*i的质因子)都在phi[i]中计算过了，因此两者的区别就只有式子开头的N，所以phi[pj * i] = phi[i] * prime[j]
                phi[prime[j] * i] = phi[i] * prime[j];
                break;
            }
            // 这里pj - 1就是(1 - 1 / pj) * pj
            phi[prime[j] * i] = phi[i] * (prime[j] - 1);
        }
    }
    int res = 0;
    for(int i = 1; i <= n; i ++){
        res += phi[i];
    }
    return res;
}

组合数

组合数1

主要思想：\(C_a^b = C_{a-1}^{b-1} \times C_{a - 1}^{b}\)

时间复杂度：O(n^2)

int c[N][N];

void init(){
    for(int i = 0; i < N; i ++){
        for(int j = 0; j <= i; j ++){
            if(j == 0) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
        }
    }
}

组合数2

预处理阶乘

int fact[N], infact[N];//存的分别是i的阶乘及其逆元

// 求a^k mod p
int qPow(int a, int k, int p) {
    int res = 1;
    while (k) {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

{
    fact[0] = infact[0] = 1;
    for (int i = 1; i < N; i ++) {
        fact[i] = (LL) fact[i - 1] * i % mod;
        infact[i] = (LL) infact[i - 1] * qmi(i, mod - 2, mod) % mod;
    }
    int a, b;
    scanf("%d%d", &a, &b);
    //这里要及时取模，否则会爆long long
    printf("%d\n", (LL) fact[a] * infact[b] % mod * infact[a - b] % mod);
    }
}

博弈论

必胜态：从这个状态总是有某种方式走到一个必败态

必败态：从这个状态无论怎么走都是会走到必胜态

如果先手初始处于必败态，那么先手必败，反之先手必胜

SG函数

首先，我们定义一个mex函数（或者称为mex操作）：

\(mex(A)\): 返回A集合中未曾出现过的最小的自然数

\(sg(x)\): 如果处于最终态，则返回0；否则返回该节点可以到达的状态（A集合）中未曾出现过的最小的自然数

图论

最短路

Dijkstra求最短路(朴素版)

Dijkstra算法总体流程：

1. dist[1] = 0, dist[i] = +\(\infty\)
2. for i : 1 ~ n
   • t\(\leftarrow\)不在s中的距离最近的点（其中s表示当前已确定最短距离的点的集合）\(\color{green}{O(n^2)}\)
   • s\(\leftarrow\) t \(\ \color{green}{n \times O(1)}\)
   • 用t更新其他点的距离 \(\ \color{green}{O(m)}\)

朴素版dijkstra算法时间复杂度是O（\(n^2\)）（其中n代表图中点的个数）

因此适合用于稠密图，即边多点少的图

int n, m;
int g[N][N]; //存储图，g[i][j]的值是i到j的距离，因为是稠密图，所以用邻接矩阵来存
int dist[N]; //dist[i]存的是i节点到1节点的最短距离
int st[N];   //st[i]为true说明i节点的值是最小距离

int dijkstra(){
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    //循环n-1次，即更新n-1次st[?]，这样就把1到1~n这n个节点的最短路都算出来了
    for(int i = 1; i <= n - 1; i ++){
        int t = -1;
        //找到未存入最短值且到1节点距离最短的节点t
        for(int j = 1; j <= n; j++){
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        }
        //if(t == n) goto end;这个优化只有这题能加，意思是当求得1到n的最短路时，即可break，因为这就是题目所求
        st[t] = true;
        //用t节点来更新其他节点（不是t的邻点的话他的g[t][j]就为无穷）
        for(int j = 1; j <= n; j ++){
            dist[j] = min(dist[j], dist[t] + g[t][j]);
        }
    }
    //end:
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

堆优化的Dijkstra算法

堆优化版Dijkstra算法总体流程：

1. dist[1] = 0, dist[i] = +\(\infty\)
2. for i : 1 ~ n
   • t\(\leftarrow\)不在s中的距离最近的点（其中s表示当前已确定最短距离的点的集合）\(\color{green}{O(n)}\)
   • s\(\leftarrow\) t \(\ \color{green}{O(n)}\)
   • 用t更新其他点的距离 \(\ \color{green}{O(mlog(n))}\)

堆优化版dijkstra算法时间复杂度是O（\(mlog(n)\)）（其中n代表图中点的个数, m代表边的个数）

\(\color {red} {因此适合用于稀疏图，即边少点多的图}\)

typedef pair<int, int> PII;

int h[N], e[N], ne[N], idx;
int w[N];
int dist[N];
bool st[N];
int n, m;

void add(int x, int y, int c){
    w[idx] = c;
    e[idx] = y;
    ne[idx] = h[x];
    h[x] = idx++;
}

int dijkstra(){
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});
    while(heap.size()){
        PII k = heap.top();
        heap.pop();
        int ver = k.second, distance = k.first;
        if(st[ver]) continue;
        st[ver] = true;
        for(int i = h[ver]; i != -1; i = ne[i]){
            int j = e[i];
            if(dist[j] > distance + w[i]){
                dist[j] = distance + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

SPFA

spfa算法

底子是： for 所有边a，b，w

dist[b] = min(dist[b], dist[a] + w)

流程是：

queue \(\leftarrow\) 1

while queue不空：

1. t\(\leftarrow\)queue.front(), q.pop();

2. 更新t的所有出边t\(\stackrel{w}{\longrightarrow}\)b, q\(\leftarrow\)b;

spfa求最短路不能处理有自环负权和负权环的情况，这两种情况会在while循环中卡住，所以这题数据不太强

1.stl queue

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N]; // st数组是判断当前节点是否在队列当中，防止重复入队

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int spfa() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    queue<int> q;
    q.push(1);
    st[1] = true;
    while (q.size()) {
        int t = q.front();
        q.pop();
        st[t] = false;
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                if (!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    return dist[n];
}

{
    memset(h, -1, sizeof h);
    int t = spfa();
    if (t == 0x3f3f3f3f) puts("impossible");
    else printf("%d\n", t);
}

循环队列

int n, m, S, T;
int h[N], e[M], w[M], ne[M], idx;
int dist[N], q[N];
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

void spfa() {
    memset(dist, 0x3f, sizeof dist);
    dist[S] = 0;
    // hh指向队头元素，tt指向队尾元素的后一个元素。
    int hh = 0, tt = 1;
    q[0] = S, st[S] = true;
    while(hh != tt){
        int t = q[hh++];
        if(hh == N) hh = 0;
        st[t] = false;
        for(int i = h[t]; ~i; i = ne[i]){
            int j = e[i];
            if(dist[j] > dist[t] + w[i]){
                dist[j] = dist[t] + w[i];
                if(!st[j]){
                    q[tt++] = j;
                    if(tt == N) tt = 0;
                    st[j] = true;
                }
            }
        }
    }
}

{
    memset(h, -1, sizeof h);
    spfa();
    cout << dist[T] << endl;
}

最小生成树

kruskal算法

int n, m;
int p[N];

struct Edge {
    int a, b, w;
    bool operator<(const Edge &W) const {
        return w < W.w;
    }
}edges[M];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);    // 路径压缩
    return p[x];
}

int kruskal() {
    sort(edges, edges + m);    // 将边按照权重从小到大排序
    for (int i = 1; i <= n; i ++ ) p[i] = i;    // 初始化并查集
    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ ) {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a), b = find(b);
        // 判断两个节点是否在同一个连通块中
        if (a != b) {
            p[a] = b;    // 将两个连通块合并
            res += w;    // 将边权重累加到结果中
            cnt ++ ;     // 记录加入生成树的边的数量
        }
    }
    if (cnt < n - 1) return INF;    // 判断生成树中是否包含n-1条边
    return res;
}

{
    for (int i = 0; i < m; i ++ ) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        edges[i] = {a, b, w};
    }
    int t = kruskal();
    if (t == INF) puts("impossible");    // 无法生成最小生成树
    else printf("%d\n", t);             // 输出最小生成树的权重
}

Kruskal算法是一种贪心算法，其正确性可以通过贪心选择性质的证明得到。

假设我们要构造一个无向连通图的最小生成树。我们定义一个边集\(E\)为“好的”，如果它是某棵最小生成树的子集。我们定义一个边集\(E\)为“坏的”，如果它包含了某个环上的边。

首先我们考虑一个引理：对于任何的连通图，\(E\)为“好的”，则\(E\)中的边是没有环的。

证明：如果\(E\)中存在环，则我们可以从中删去任意一条边，得到一个更小的\(E\)集合，仍然满足“好的”性质。因此，在“好的”边集中，所有的边都没有构成环。

然后我们考虑另一个引理：对于任何的连通图，令\(E\)为“好的”边集合，令\(e\)为一条“好的”边，并令\(E'=E \backslash {e}\)。则\(E'\)为某棵生成树的子集。

证明：因为\(e\)为“好的”边，所以\(E\)中不包含\(e\)的时候，\(E\)仍然是连通的。因此，\(E'\)也是连通的。由于\(E'\)中没有环，所以它也是无向无环图，也就是一棵树。此外，\(E'\)中有\(n-1\)条边，与任何生成树的边数相同，所以\(E'\)也是某棵生成树的子集。

有了上面的两个引理，我们可以得到Kruskal算法的正确性证明：

1. 初始化\(E\)为空集；
2. 将所有边按照权值从小到大排序；
3. 依次考虑每条边\(e\)，如果将其加入\(E\)不会产生环，则将其加入\(E\)中；
4. 当加入了\(n-1\)条边后，停止算法。此时\(E\)即为一棵生成树。

根据引理1，\(E\)中所有的边没有环；根据引理2，算法停止时，\(E\)为某棵生成树的子集；根据Kruskal算法的贪心选择性质，我们知道\(E\)为全局最优的“好的”边集合，因此\(E\)中的边必定构成了一棵最小生成树。

因此，Kruskal算法的正确性得证。

LCA(最近公共祖先)

倍增法求LCA的步骤为：

• 把两个点跳到同一层, 即把下面的x跳到和y同一层
• 在depth[x] == depth[y]之后，
  1. x == y 则该点就是x和y的最近公共祖先
  2. x != y 即他俩同层但不相同，则继续让两个点同时往上跳，一直跳到他们的最近公共祖先的下面一层

这里跳到最近公共祖先的下一层是因为不这样做的话有可能我们某一次跳过头了，跳过了lca, 来到了lca的某一个祖宗节点上，这样我们就无法判断lca在现处节点下面的哪一层上了

// depth表示某个节点在树中的深度，其中根节点的dpeth为1, 越往下深度越大。
// fa[i][k]指节点i向上走2^k布所能到达的节点。
// fa的第二个参数，是向上走的最大距离取log下取整，这里是对点数4e4取log得15
int depth[N], fa[N][16];

// 通过宽搜来初始化depth和fa数组。
void bfs(int root) {
    queue<int> q;
    memset(depth, 0x3f, sizeof depth);
    // 这里depth[0] = 0起哨兵作用，以防跳出根节点之上。
    depth[0] = 0, depth[root] = 1;
    q.push(root);
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (depth[j] > depth[t] + 1) {
                depth[j] = depth[t] + 1;
                q.push(j);
                fa[j][0] = t;
                for (int k = 1; k <= 15; k ++) {
                    fa[j][k] = fa[fa[j][k - 1]][k - 1];
                }
            }
        }
    }
}

int lca(int a, int b) {
    if (depth[a] < depth[b]) swap(a, b);
    for (int k = 15; k >= 0; k --) {
        if (depth[fa[a][k]] >= depth[b]) {
            a = fa[a][k];
        }
        // 使a尽量跳到和b同层，并最终一定能跳到。
    }
    if (a == b) return a;
    for (int k = 15; k >= 0; k --) {
        if (fa[a][k] != fa[b][k]) {
            a = fa[a][k];
            b = fa[b][k];
        }
    }
    return fa[a][0];
}

dfs版本预处理

同时顺便求出每个节点向上对应步数的最小的边权

void dfs(int u, int fa) {
    depth[u] = depth[fa] + 1;
    f[u][0] = fa;
    for (int i = 1; 1 << i < depth[u]; i ++) {
        f[u][i] = f[f[u][i - 1]][i - 1];
        minv[u][i] = min(minv[f[u][i - 1]][i - 1], minv[u][i - 1]);
    }
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa) continue;
        minv[j][0] = w[i];
        dfs(j, u);
    }
}

数据结构

链表

单链表（静态）

//head是头指针，e存权值，ne存下一个节点，idx分配节点
int head, e[N], ne[N], idx;

void init(){
    head = -1; //链表中最后一个节点的ne始终是-1
    idx = 0;
}

void add_to_head(int x){ //在头结点前建立节点
    e[idx] = x;
    ne[idx] = head;
    head = idx ++;
}

void add_to_k(int k, int x){
    e[idx] = x;
    ne[idx] = ne[k];
    ne[k] = idx ++;
}

void remove(int k){
    ne[k] = ne[ne[k]];
}

双链表

int r[N], l[N], e[N], idx;

//1节点和0节点相当于变相的head指针，没有e值
void init(){
    r[0] = 1;
    l[1] = 0;
    idx = 2;
}

//在k节点的右边插入值为x的节点
void insert(int k, int x){
    e[idx] = x;
    l[idx] = k;
    r[idx] = r[k];
    l[r[k]] = idx; //必须先做这个，否则后面的r[k]会被修改掉
    r[k] = idx;
    idx ++;
}

void remove(int k){
    r[l[k]] = r[k];
    l[r[k]] = l[k];
}

队列

一般队列

int hh = 0, tt = -1;
int q[N];

void push(int x) {
    q[++tt] = x;
}

void pop() {
    hh++;
}

int front() {
    return q[hh];
}

循环队列

主要在bfs及spfa算法中使用

void bfs(int x) {
    int q[N];
    int hh = 0, tt = 0;
    q[tt++] = x;
    st[x] = true;
    while (hh != tt) {
        int t = q[hh++];
        if (hh == N) hh = 0;
        for () {

        }
    }
}

单调队列

以滑动窗口为例

int n, k; // k代表滑动窗口的长度
int a[N], q[N];
int hh, tt;

{
    hh = 0, tt = -1;
    for (int i = 1; i <= n; i ++) {
        if (hh <= tt && q[hh] < i - k + 1) hh ++;
        while (hh <= tt && a[q[tt]] >= a[i]) tt --;
        q[++ tt] = i;
        if(i >= k) printf("%d ", a[q[hh]]);
    }
}

栈

一般栈

int m;
int stack[N], tt;

void push(int x) {
    stack[++ tt] = x;
}

void pop() {
    tt --;
}

bool empty() {
    if (tt > 0) return false;
    return true;
}

int query() {
    return stack[tt];
}

表达式求值

stack<int> num;
stack<char> op;

void eval(){
    auto b = num.top(); num.pop();
    auto a = num.top(); num.pop();
    auto c = op.top(); op.pop();
    int x;
    if(c == '+') x = a + b;
    else if (c == '-') x = a - b;
    else if (c == '*') x = a * b;
    else x = a / b;
    num.push(x);
}

{
    unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};
    string str;
    cin >> str;
    for (int i = 0; i < str.size(); i ++) {
        auto c = str[i];
        if (isdigit(c)) {
            int x = 0, j = i;
            while (j < str.size() && isdigit(str[j]))
                x = x * 10 + str[j ++] - '0';
            i = j - 1;
            num.push(x);
        }
        else if (c == '(') op.push(c);
        else if (c == ')') {
            while (op.top() != '(') eval();
            op.pop();
        }
        else {
            while (op.size() && pr[op.top()] >= pr[c]) eval();
            op.push(c);
        }
    }
    while (op.size()) eval();
    cout << num.top() << endl;
}

单调栈

int stk[N], tt;
int n;
int a[N];

{
    cin >> n;
    for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++) {
        while (tt && stk[tt] >= a[i]) tt --;
        if (tt) cout << stk[tt] << ' ';
        else cout << -1 << ' ';
        stk[++ tt] = a[i];
    }
}

KMP

int n, m;
char s[1000010], p[100010];
int ne[100010];
// ne[1] = 0, ne[2]的值不确定，注意next数组的定义可能会有多种
// 有些定义下的ne[2]的值必定是1

{
    cin >> n >> p + 1 >> m >> s + 1;
    //构造next数组，存储最大公共前后缀
    //i从2开始，默认ne[1] = 0.
    for (int i = 2, j = 0; i <= n; i ++) {
        //求ne[i]的时候ne[i - 1]已经求出来了, 此时j和i-1对齐
        while (j && p[i] != p[j + 1]) j = ne[j]; //j回滚到当前前缀串的最大公共前缀串
        if (p[i] == p[j + 1]) j ++; //p[i]与p[j + 1]匹配成功，可以匹配下一个位置, 这里让匹配好的j(p串匹配好的字符数)变成j + 1
        ne[i] = j;
    }
    //匹配sp
    for (int i = 1, j = 0; i <= m; i ++) {
        while (j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j++;
        if (j == n) {
            printf("%d ", i - j);
            j = ne[j];
        }
    }
}

TRIE

const int N = 100010; //存的是所有节点的最大个数

int n;
int son[N][26], cnt[N], idx;

void insert(char str[]) {
    int p = 0;  // 每次从根节点开始找
    for (int i = 0; str[i]; i ++) {
        int u = str[i] - 'a';
        if (!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];
    }
    cnt[p] ++; //标记不是打在要插入的字符串的最后一个字母对应的节点的下一个节点上的***
}

int query(char str[]) {
    int p = 0;
    for (int i = 0; str[i]; i ++) {
        int u = str[i] - 'a';
        if (!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

堆

int n;
int h[N], pk[N], kp[N];
int idx, len; //idx是用来维护第几个插入堆中的点

void hswap(int a, int b){
    swap(h[a], h[b]);
    swap(pk[a], pk[b]);
    swap(kp[pk[a]], kp[pk[b]]);
}

void up(int u){
    while(u / 2 && h[u] < h[u / 2]){
        hswap(u, u / 2);
        u /= 2;
    }
}

void down(int u){
    int t = u;
    if(u * 2 <= len && h[u * 2] < h[t]) t = u * 2;
    if(u * 2 + 1 <= len && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if(u != t){
        hswap(u, t);
        down(t);
    }
}

void insert(int x){
    h[++len] = x;
    pk[len] = ++idx;
    kp[idx] = len;
    up(len);
}

void delmin(){
    hswap(1, len);
    len --;
    down(1);
}

void del(int u){
    hswap(u, len);
    len --;
    down(u);
    up(u);
}

// void del(int k){
//     int t = kp[k];
//     hswap(kp[k], len);
//     len --;
//     up(t);
//     down(t);
// }

void change (int u, int x){
    h[u] = x;
    up(u), down(u);
}

并查集

//p[i]存储i节点的祖宗节点，d[i]存储i节点到祖宗节点的距离
int p[N], d[N];

//初始化
void init() {
    for (int i = 0; i <= n; i ++) {
        p[i] = i;
        d[i] = 0;
    }
}

//找祖宗节点，同时更新d数组
int find(int x) {
    if (x != p[x]) {
        int t = find(p[x]);
        //x到祖宗的距离=x到p[x]的距离+p[x]到祖宗的距离
        //这里的距离更新仅仅是更新的d[x]正确（找祖先）的情况下，在做并差集合并时还得手动更新
        d[x] = d[x] + d[p[x]];
        p[x] = t;
    }
    return p[x];
}

int find (int x) {
    if(x != p[x]) p[x] = find(p[x]);
    return p[x];
}

哈希表

模拟

拉链法

int h[N], e[N], ne[N], idx;

void insert(int x) {
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx++;
}

bool find(int x) {
    int k = (x % N + N) % N;
    for(int i = h[k]; i != -1; i = ne[i]){
        if(e[i] == x)
            return true;
    }
    return false;
}

开放寻址法

const int N = 200003, null = 0x3f3f3f3f;

int a[N];

int find(int x) {
    int k = (x % N + N) % N;
    while(a[k] != null && a[k] != x){
        k ++;
        if(k == N) k = 0;
    }
    return k;
}

树状数组和线段树

树状数组

“树状数组的下标从1开始,不可以从0开始,因为lowbit(0)=0时会出现死循环”

int n, m;
int a[N];
int tr[N];

int lowbit(int x) {
    //lowbit这个函数的功能就是求某一个数的二进制表示中最低的一位1，举个例子，
    //x = 6，它的二进制为110，那么lowbit(x)就返回2，因为最后一位1表示2
    return x & -x;
}

void add(int x, int v) {
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

int query(int x) { //求1~x的和
    int res = 0;
    for(int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

线段树

int n, m;
int w[N];
struct Node{
    int l, r;
    int sum;
}tr[N * 4];

void pushup(int u) {
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}

void build(int u, int l, int r) {
    if (l == r) tr[u] = {l, r, w[r]};
    else {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

int query(int u, int l, int r) {
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
    int mid = tr[u].l + tr[u].r >> 1;
    int sum = 0;
    if (l <= mid) sum = query(u << 1, l, r);
    if (r > mid) sum += query(u << 1 | 1, l, r);
    return sum;
}

void modify(int u, int x, int v){
    if (tr[u].l == tr[u].r) tr[u].sum += v;
    else{
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

树链剖分（重链剖分）

将树中任意一条路径转化为\(O(logn)\)段连续区间

1. 将一棵树转化为一个序列
2. 树中路径转化为\(logn\)段连续区间

dfs序（dfn）：优先遍历重儿子，即可保证重链上所有点的编号是连续的，注意这里的dfs是按照优先遍历重儿子来的dfs序

定理：树中任意一条路径均可拆分成\(O(logn)\)条重链，即可拆分成\(O(logn)\)段连续区间

重儿子：某个节点的所有子树中size最大的那个的父节点是当前节点的重儿子，其他节点为轻儿子

重边：重儿子往他的父节点去的边

轻边：其他所有边

重链：重边构成的极大的一条链

重儿子所在的重链的top是他往上的轻儿子，轻儿子所在的重链的top是他自己

int w[N], h[N], e[M], ne[M], idx;
int id[N], nw[N], cnt;
int dep[N], sz[N], top[N], fa[N], son[N];

// 预处理出来每个点的重儿子，深度，所在子数大小
void dfs1(int u, int father, int depth) {
    dep[u] = depth, fa[u] = father, sz[u] = 1;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == father) continue;
        dfs1(j, u, depth + 1);
        sz[u] += sz[j];
        if (sz[son[u]] < sz[j]) son[u] = j;
    }
}

// 算出每个节点的dfn序，每个节点所在的重链的顶点是谁
void dfs2(int u, int t) {
    id[u] = ++cnt, nw[cnt] = w[u], top[u] = t;
    if (!son[u]) return;
    dfs2(son[u], t);
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa[u] || j == son[u]) continue;
        dfs2(j, u);
    }
}

树上启发式合并

用同一套数组（当然也可以是其他数据结构）来记录所有子树的信息，在更新新的子树信息前把当前子树的信息存下来。

一般地思考的话，我们可以在每次算完当前子树信息，将要回溯的时候，把数组全部清空，但是这样时间复杂度会达到n^2级别，因此考虑优化。

结论：每次先算轻儿子为根的子树，再算重儿子为根的子树，利用重儿子为根的子树的信息来更新当前节点为根的子树的信息。并且在算完轻儿子为根的子树的信息后清空信息。这样可以把时间复杂度压缩为\(O(logn)\)

为什么呢？

考虑每个节点对答案的贡献次数，即搜索次数, 即这个点所在的所有子树中，有多少棵会被遍历。由遍历策略导致，只有轻儿子为根的子树才会被重复遍历。因此贡献次数取决于当前节点所在的子树中有多少棵子树是他父节点的轻儿子。换句话来说，就是当前节点到根节点的路径中，有多少条边是轻边。由树链剖分的性质可知最多有\(logn\)条轻边。

为什么是logn条轻边呢？

因为我们从当前点往上走，每走一条轻边，子树的元素个数至少乘2，因为上面的父节点会有重儿子且不是当前节点。所以最多只能走logn条轻边。

void dfs0(int u, int fa) {
    sz[u] = 1;
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa) continue;
        dfs0(j, u);
        sz[u] += sz[j];
        if (sz[j] > sz[son[u]]) son[u] = j;
    }
}

// pson代表当前u的重儿子，即不要重复算重儿子的部分
void update(int u, int fa, int sign, int pson) {
    cnt[c[u]] += sign;
    if (cnt[c[u]] > mx) mx = cnt[c[u]], sum = c[u];
    else if (cnt[c[u]] == mx) sum += c[u];
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa || j == pson) continue;
        update(j, u, sign, pson);
    }
}

// op代表u是重儿子还是轻儿子
void dfs(int u, int fa, int op) {
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == fa || j == son[u]) continue;
        dfs(j, u, 0);
    }
    if (son[u]) dfs(son[u], u, 1);
    update(u, fa, 1, son[u]);
    ans[u] = sum;
    if (!op) update(u, fa, -1, 0), sum = mx = 0;
}

莫队

基础莫队

本质是通过排序优化了普通尺取法的时间复杂度。

考虑如果某一列询问的右端点是递增的，那么我们更新答案的时候，右指针只会从左往右移动，那么i指针的移动次数是\(O(n)\)的。

当然，我们不可能让左右端点都单调来做到总体\(O(n)\)。

考虑对左端点进行分块。

莫队排序：

左端点按照分块的编号来排，如果分块编号不同的话编号较小的靠前，如果相同的话右端点小的在前。可以证明这样排完序的话时间复杂度可以做到\(O(n \sqrt n)\)。

这样我们把区间分成了\(\sqrt n\)块，每块的长度都是\(\sqrt n\)，在每一块内部，所有查询的右端点是递增的。

右指针：在每一块内部，右端点递增，所以右端点走的总数不会超过\(n\)（注意每一块内部放的是左端点，右端点是完全有可能超出这个块的范围的，因此这里为\(n\)），一共有\(\sqrt n\)块，所以右端点总共走的次数不会超过\(n \sqrt n\)。

左指针：先考虑每一次询问：

1. 左指针在块内部移动，块的长度是\(\sqrt n\)，因此最多只会移动\(\sqrt n\)次。

2. 左指针在相邻两块之间移动，最坏是从第一个块的左端点移动到第二个块的右端点，因此最坏移动\(2 \sqrt n\)次。

因为有q次询问，所以1是\(q \sqrt n\)，2是\(2n\)。

因为一共有\(\sqrt n\)个块，我们从前往后要跨过\(\sqrt n - 1\)次，每次最多是\(2 \sqrt n\)，所以时间复杂度是\(2n\)。

所以总时间复杂度为\(O(q \sqrt n)\)。

玄学优化

奇数块：块内按照右端点从小到大排。

偶数快：块内按照右端点从大到小排。

二者可以互换。

前一段从左到右滚，右端点从左滚到了右边接近n的位置，下一次从右到左滚，可以更方便一些，相当于更加顺路了。

如果我们块的大小是\(a\)的话，那么块的数量就是\(\frac{n}{a}\)，那么r的复杂度就是\(\frac{n}{a}n = \frac{n^2}{a}\)，l的复杂度是\(qa\)（只考虑块内），总复杂度为两者之和，当两者相等时取得最小值，解得\(a = \sqrt{\frac{n^2}{q}}\)。

// 代码为统计一段区间上是否有不相同的数，没有输出yes
int n, q;
int a[N];
vector<array<int, 3>> v;
int cnt[210];
int ans[N];
int len;

int get(int x) {
    return x / len;
}

void adds(int x, int &res) {
    if (!cnt[x]) res ++;
    cnt[x] ++;
}

void del(int x, int &res) {
    cnt[x] --;
    if (!cnt[x]) res --;
}

void solve() {
    cin >> n >> q;
    len = max(1, (int)sqrt((double)n * n / q));
    for (int i = 1; i <= n; i ++) {
        cin >> a[i];
        a[i] += 100;
    }
    for (int i = 1; i <= q; i ++) {
        int l, r;
        cin >> l >> r;
        v.push_back({i, l, r});
    }
    auto cmp = [&](array<int, 3> &a, array<int, 3> &b) {
        int i = get(a[1]), j = get(b[1]);
        if (i != j) return i < j;
        return a[2] < b[2];
    };
    sort(v.begin(), v.end(), cmp);
    // i是右指针，j是左指针
    for (int k = 0, i = 0, j = 1, res = 0; k < q; k ++) {
        int id = v[k][0], l = v[k][1], r = v[k][2];
        while (i < r) adds(a[++ i], res);
        while (i > r) del(a[i --], res);
        while (j < l) del(a[j ++], res);
        while (j > l) adds(a[-- j], res);
        ans[id] = res;
    }
    for (int i = 1; i <= q; i ++)
        if (ans[i] == 1) cout << "YES\n";
        else cout << "NO\n";
}

双set实现对顶堆

multiset<int> s1, s2;
int l, r, mid;
int bal = 0;

void init() {
    s1.clear();
    s2.clear();
    s1.insert(-LLF);
    s2.insert(LLF);
    l = r = mid = 0;
    bal = 0;
}

void add(int x) {
    if (!bal) {
        int a = *(--s1.end());
        int b = *s2.begin();
        if (a <= x && x <= b) {
            mid = x;
        }
        else if (a > x) {
            s1.erase(s1.find(a));
            s1.insert(x);
            l += x - a;
            mid = a;
        }
        else if (b < x) {
            s2.erase(s2.find(b));
            s2.insert(x);
            r += x - b;
            mid = b;
        }
    }
    else {
        if (x >= mid) {
            s1.insert(mid);
            l += mid;
            s2.insert(x);
            r += x;
        }
        else {
            s2.insert(mid);
            r += mid;
            s1.insert(x);
            l += x;
        }
    }
    bal ^= 1;
}

void del(int x) {
    int a = *(--s1.end());
    int b = *s2.begin();
    if (!bal) {
        if (a >= x) {
            s1.erase(s1.find(x));
            l -= x;
            s2.erase(s2.find(b));
            r -= b;
            mid = b;
        }
        else {
            s2.erase(s2.find(x));
            r -= x;
            s1.erase(s1.find(a));
            l -= a;
            mid = a;
        }
    }
    else {
        if (mid == x) {}
        else if (x > mid) {
            s2.erase(s2.find(x));
            s2.insert(mid);
            r += mid - x;
        }
        else {
            s1.erase(s1.find(x));
            s1.insert(mid);
            l += mid - x;
        }
        mid = 0;
    }
    bal ^= 1;
}

动态规划

最长上升子序列

1.朴素版本

int n;
int a[N];
int dp[N]; //dp中存的是以a[i]结尾的子序列的集合中最长的子序列的长度

{
    for(int i = 1; i <= n; i ++){
        dp[i] = 1;
        for(int j = 1; j < i; j ++){
            if(a[j] < a[i]){
                dp[i] = max(dp[i], dp[j] + 1);
            }
        }
    }
    int ans = 0;
    for(int j = 1; j <= n; j ++) ans = max(ans, dp[j]);
    cout << ans;
}

2.1模拟栈版本

{
    vector<int> arr(n);
    vector<int> stk;//模拟堆栈
    stk.push_back(arr[0]);
    for (int i = 1; i < n; ++i) {
        if (arr[i] > stk.back()) //如果该元素大于栈顶元素,将该元素入栈
            stk.push_back(arr[i]);
        else //替换掉第一个大于或者等于这个数字的那个数
            *lower_bound(stk.begin(), stk.end(), arr[i]) = arr[i];
    }
    cout << stk.size() << endl;
}

2.2二分写法

int n;
int a[N];
int q[N];

{
    int len = 0;
    for (int i = 0; i < n; i ++) {
        int l = 0, r = len;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (q[mid] < a[i]) l = mid;
            else r = mid - 1;
        }
        len = max(len, r + 1);
        q[r + 1] = a[i];
    }
    printf("%d\n", len);
}

附：最长不下降子序列

void subseq1(int a[], int l, int r) { // 对原数组的每个下标i(从1开始)，求以a[i]结尾的最长不下降子序列长度
    int len = 0;
    // q下标从2开始才放如元素,q[i]是有长度为i-1的子序列的最小的末尾值
    for (int i = l; i <= r; i ++) {
        int ll = l, rr = len + 1;
        while (ll < rr) {
            int mid = ll + rr + 1 >> 1;
            if(q[mid] <= a[i]) ll = mid;
            else rr = mid - 1;
        }
        len = max(len, rr);
        q[rr + 1] = a[i];
    }
    // 二分求出以a[i]结尾的最长不下降子序列长度
    for (int i = l; i <= r; i ++) {
        int l2 = 2, r2 = len + 1;
        while (l2 < r2) {
            int mid = l2 + r2 + 1 >> 1;
            if(q[mid] <= a[i]) l2 = mid;
            else r2 = mid - 1;
        }
        dp1[i] = l2 - 1;
    }
}

背包问题

01背包

状态表示：\(f[i][j]\):在前i个物品中选，总体积不超过j的最大价值。

01背包问题的二维代码

{
    //动态规划问题一般下标从1开始，便于从0的情况递推结果。
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) {
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            }
        }
    }
}

01背包一维优化

{
    for (int i = 1; i <= n; i ++) {
        for (int j = m; j >= v[i]; j --) {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
}

完全背包问题

特征：一个物品可以选无数次。

状态表示：\(f[i][j]\)表示从前i个物品里选择（一个物品可以选多次），总体积不超过j的最大价值。

完全背包问题的三重循环代码

{
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            for (int k = 0; k * v[i] <= j; k ++) {
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
            }
        }
    }
}

二重循环二维的优化过程

// 01
f[i][j]        = max(f[i][j],            f[i - 1][j - k * v[i]] + k * w[i]);
// 完全
f[i][j]        = max(f[i - 1][j],        f[i - 1][j - v[i]] + w[i], f[i - 1][j - 2 * v[i]] + 2 * w[i], .....)
f[i][j - v[i]] = max(f[i - 1][j - v[i]], f[i - 1][j - 2 * v[i]] + 1 * w[i], .....)

三式代入二式，得：

f[i][j] = max(f[i - 1][j],f[i][j - v[i]] + w[i]);

{
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) {
                f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
            }
        }
    }
}

完全背包一维最终优化

{
    for (int i = 1; i <= n; i ++) {
        for (int j = v[i]; j <= m; j ++) {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
}

多重背包1

特征：一个物品有严格的次数限制。

状态表示：\(f[i][j]\)表示从前i个物品里选择（一个物品有严格的次数限制），总体积不超过j的价值；

多重背包问题的三重循环代码

//s[i]表示第i种物品共有s[i]个
int f[N][N], s[N], v[N], w[N];

{
    for (int i = 1; i <= n; i ++) {
        for (int j = 1; j <= m; j ++) {
            for (int k = 0; k <= s[i] && k * v[i] <= j; k ++) {
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
            }
        }
    }
}

多重背包问题一维优化代码

{
    for (int i = 1; i <= n; i ++) {
        for (int j = m; j >= v[i]; j --) {
            for (int k = 0; k <= s[i] && k * v[i] <= j; k ++) {
                f[j] = max(f[j], f[j - k * v[i]]+ k * w[i]);
            }
        }
    }
}

多重背包问题打包版

利用二进制优化的思想，把同一种类型的物品按照2的不同次幂个为一组进行打包，从而优化时间复杂度。

时间复杂度：\(O(nmlogs)\)

// s[i]存储第i种物品的个数
// a, b数组存的是原体积和原价值
int a[N], b[N];
int v[N], w[N], s[N];

{
    int cnt = 0;
    for (int i = 1; i <= n; i ++) {
        int k = 1;
        int ss = s[i];
        while (k <= s) {
            cnt ++;
            v[cnt] = k * a[i];
            w[cnt] = k * b[i];
            s -= k;
            k *= 2;
        }
        if (s > 0) {
            cnt ++;
            v[cnt] = s * a;
            w[cnt] = s * b;
        }
    }
    for (int i = 1; i <= cnt; i ++) {
        for (int j = m; j >= v[i]; j --) {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
}

多重背包单调队列优化

时间复杂度：\(O(nm)\)

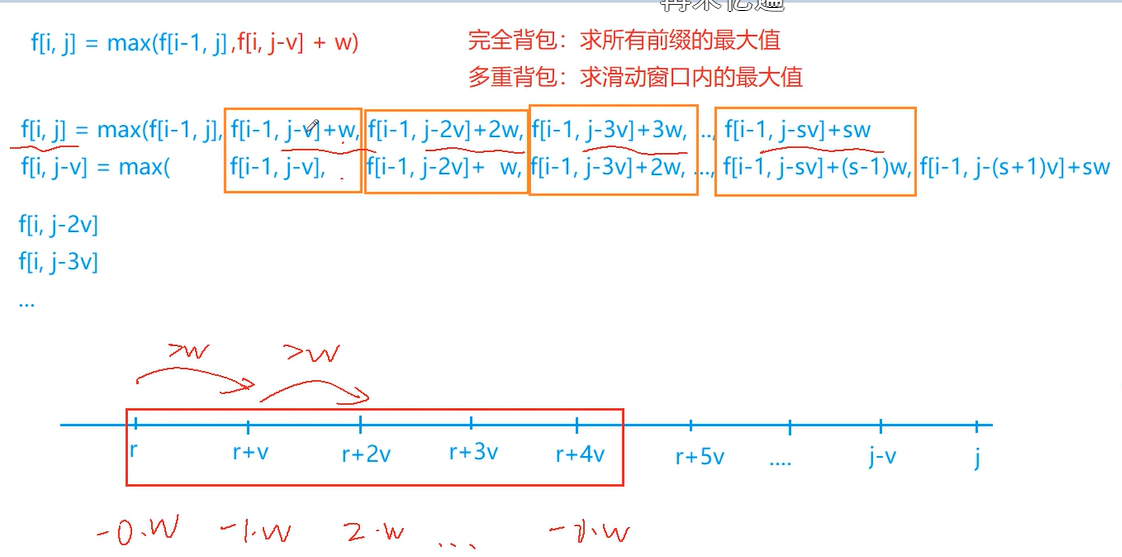
int f[N];
int g[N]; // g是f的滚动数组
int v[N], w[N], s[N];

{
    for (int i = 1; i <= n; i ++) {
        memcpy(g, f, sizeof f); //把上一层的f存在g里
        for (int j = 0; j < v[i]; j ++) {
            int hh = 0, tt = -1;
            //滑动窗口长度为s，不包括f[k]本身，因此f[k] = max(f[k], max(others))
            for (int k = j; k <= m; k += v[i]) {
                if (hh <= tt && q[hh] < k - s[i] * v[i]) hh ++;
                if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v[i] * w[i]);
                //由图中表达式知g数组中的值都是不包含w的，这里我们进行比较只需比较绝对值
                //因此只要营造出递减数列的效果即可
                while (hh <= tt && g[q[tt]] - (q[tt] - j) / v[i] * w[i] <= g[k] - (k - j) / v[i] * w[i]) tt --;
                q[++tt] = k;
            }
        }
    }
}

分组背包问题

特征：一组物品只能选择其中的一个。

状态表示：f[i][j]表示从前i组物品里选择(一组物品最多只能选择其中的一个)，总体积不超过j的最大价值；

状态计算：f[i][j]=max(f[i-1][j],f[i-1][j-w[i][k]]+v[i][k])(解释；表示从前i组物品里选择体积不超过j的物品价值的最大值是从要么不选这个物品，和要么选择这个组中第k个物品的价值之间进行选择)

分组背包问题一维优化代码

// w[i][j]代表第i组物品中的第j个的价值，v同
int w[N][N],v[N][N];
// s[i]代表第i组物品有多少个
int f[N],s[N];

{
    for (int i = 1; i <= n; i ++) {
        for (int j = m; j >= 0; j --) {
            for (int k = 1; k <= s[i]; k ++) {
                if (v[i][k] <= j) {
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
                }
            }
        }
    }
    return 0;
}

背包问题中总体积最多/恰好/最少为j, 以求最大值为例(3是最小值)

1. 体积最多为j：memset(f, 0, sizeof f), v >= 0

2. 体积恰好为j：memset(f, -0x3f, sizeof f), ,f[0] = 0, v >= 0

• 怎么保证是恰好装满，通过初始化来实现, 如果不存在使f[i]满足是恰好装满的，那么这个f[i] = -INF, 即一个非法答案，就不会影响最终的计算。

1. 体积至少为j：memset(f, -0x3f, sizeof f), f[0] = 0

• f[i][j]: 从前i件物品中选，总体积至少为j的最小价值。

memset(f, 0x3f, sizeof f);

{
    for (int i = 1; i <= n; i ++) {
        for (int j = m; j >= 0; j --) {
            f[j] = min(f[j], f[max(0, j - v[i])] + w[i]);
        }
    }
}

有依赖的背包问题

\(f[u][j]\): 表示在以u为根的子树中选，且先选出u（因为其他节点都依赖u, 这样表示状态会简单一点，可以往分组背包(其实也不完全是分组背包，也就物品组和枚举决策的概念上比较像分组背包)上面套），总体积不超过j的最大价值。

void dfs(int u) {
    // 相当于分组背包问题中的物品组
    for (int u = h[u]; ~i; i = ne[i]) {
        int son = e[i];
        dfs(son);
        // 先求一下所有子树中的最大价值, 故先在最大体积中把当前节点去掉
        // 枚举体积
        for (int j = m - v[u]; j >= 0; j --) {
            // 枚举决策，这里以选取体积为多少讨论决策
            for (int k = 0; k <= j; k ++) {
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
            }
        }
    }
    // 最后记得把当前节点加上
    for (int j = m; j >= v[u]; j --) f[u][j] = f[u][j - v[u]] + w[u];
    for (int j = v[u] - 1; j >= 0; j --) f[u][j] = 0;
}

dfs(root);

混合背包问题

由于01背包、完全背包、多重背包的转移方程只和当前的第i个物品的类型有关，与前面的物品无关，所以可以对不同的类型物品独立地使用不同的状态转移方程。