文心一言 VS 讯飞星火 VS chatgpt （131）-- 算法导论11.2 3题

三、用go语言，Marley 教授做了这样一个假设，即如果将链模式改动一下，使得每个链表都能保持已排好序的顺序，散列的性能就可以有较大的提高。Marley 教授的改动对成功查找、不成功查找、插入和删除操作的运行时间有何影响?

文心一言：

Marley 教授的假设是关于调整链表（可能是一个散列链表）以保持已排序的顺序，从而提高散列的性能。这可能涉及到改变链表的查找、插入和删除操作的实现。

1.成功查找操作：如果链表保持有序，那么查找操作将更加高效。在理想情况下，查找操作的时间复杂度可以降低到O(log n)，其中n是链表的长度。这是因为在有序链表中，可以通过二分查找法快速找到目标元素。然而，在实际情况中，由于可能需要遍历整个链表来找到目标元素（特别是在链表的开头没有目标元素的情况下），所以实际的性能提升可能会受到限制。

2.不成功查找操作：对于没有找到目标元素的查找操作，有序链表的性能可能不会有明显的提升。这主要是因为无论链表是否保持有序，都需要遍历整个链表。

3.插入操作：在有序链表中插入元素的操作时间复杂度通常是O(n)，因为可能需要移动所有在目标位置之后的元素。然而，如果链表是有序的，插入操作可能会更简单一些，因为你可以避免不必要的元素移动（例如，如果你要插入的元素小于当前元素，那么你只需要把它插入到当前元素的左边）。因此，插入操作的性能可能会有所提高，但可能不会像查找操作那样明显。

4.删除操作：与插入操作类似，删除操作可能会更简单一些（例如，如果你要删除的元素大于当前元素，那么你只需要把它移动到当前元素的右边）。因此，删除操作的性能也可能会提高。

总的来说，Marley 教授的假设在理论上是有道理的，但在实际中可能受到各种因素的影响。例如，如果链表经常进行大量的插入和删除操作，那么维护链表的有序性可能会带来额外的开销。此外，如果链表的长度非常大，那么即使是O(log n)的查找操作也可能需要相当长的时间。因此，这个假设的实际效果需要具体情况具体分析。

讯飞星火：

答案：

Marley 教授的改动是将链表改为了平衡二叉搜索树（例如 AVL 树或红黑树）。这种数据结构在查找、插入和删除操作时的时间复杂度都是 O(log n)，其中 n 是树中节点的数量。相比之下，链表在这些操作上的最坏时间复杂度是 O(n)。因此，通过使用平衡二叉搜索树，我们可以显著提高散列的性能。

具体来说，Marley 教授的改动对成功查找、不成功查找、插入和删除操作的运行时间影响如下：

1.成功查找：由于使用了平衡二叉搜索树，查找操作的时间复杂度降低为 O(log n)。

2.不成功查找：由于使用了平衡二叉搜索树，不成功查找的概率会降低，但仍然需要遍历树来找到正确的位置。时间复杂度仍然是 O(log n)。

3.插入：由于使用了平衡二叉搜索树，插入操作的时间复杂度降低为 O(log n)。

4.删除：由于使用了平衡二叉搜索树，删除操作的时间复杂度降低为 O(log n)。

总之，通过使用平衡二叉搜索树，我们可以显著提高散列的性能。

360智脑：

Marley教授的假设是针对散列表的性能优化。在散列表中，数据元素的存储和查找是通过哈希函数实现的。如果链模式改动一下，使得每个链表都能保持已排好序的顺序，那么散列表的性能就可以有较大的提高。具体来说，Marley教授的改动对成功查找、不成功查找、插入和删除操作的运行时间有以下影响：

1.成功查找：在已排序的链表中，查找操作的时间复杂度为O(log n)，因为链表是按照顺序排列的，所以查找某个元素只需要遍历整个链表，最多需要log n次比较。而在无序的链表中，查找操作的时间复杂度为O(n)，因为需要从头开始遍历链表，直到找到目标元素或者遍历完整个链表。

2.不成功查找：在已排序的链表中，由于链表是按顺序排列的，所以查找失败时，只需要回溯到链表的开始位置继续查找，时间复杂度为O(1)。而在无序的链表中，查找失败时需要遍历整个链表，时间复杂度为O(n)。

3.插入操作：在已排序的链表中，插入操作的时间复杂度为O(log n)，因为在链表的头部插入新元素只需要移动后面的元素，最多需要log n次比较。而在无序的链表中，插入操作的时间复杂度为O(n)，因为需要将后面的元素全部向右移动，最多需要移动n个元素。

4.删除操作：在已排序的链表中，删除操作的时间复杂度为O(log n)，因为在链表的尾部删除元素只需要移动前面的元素，最多需要log n次比较。而在无序的链表中，删除操作的时间复杂度为O(n)，因为需要将后面的元素全部向前移动，最多需要移动n个元素。

因此，Marley教授的改动可以使散列表的性能得到较大的提高，特别是对于成功查找和插入操作，可以提高其效率。但对于不成功查找和删除操作，改动并不会有明显的提升。

智谱清言：

在 Go 语言中，Marley 教授对链模式的改动可能会影响成功查找、不成功查找、插入和删除操作的运行时间。以下是具体的影响：

1.成功查找：

如果链表保持已排好序的顺序，那么在成功查找的情况下，运行时间可能会得到提高。因为有序的链表可以减少查找的时间复杂度，从而提高查找效率。当数据按照散列值的大小顺序排列时，查找特定值的过程可能会更快，因为不需要遍历整个链表，而只需在相应散列值的范围内进行查找。

2.不成功查找：

对于不成功查找，改动后的链表仍然需要遍历整个链表来查找不存在的值。由于链表保持有序，查找过程可能会相对较快，但总体运行时间仍然取决于链表的长度。因此，不成功查找的运行时间可能会在一定程度上得到提高，但提高程度可能不如成功查找明显。

3.插入操作：

插入操作的运行时间可能会受到一定程度的影响。由于链表保持有序，插入新值时需要找到合适的位置，这可能需要移动部分元素。然而，由于 Go 语言的并发支持，插入操作可以在一定程度上并行执行，从而减小总体运行时间。总体来说，插入操作的运行时间可能会受到一定程度的影响，但具体取决于插入操作的频率和链表的长度。

4.删除操作：

删除操作的运行时间也可能会受到一定程度的影响。在有序链表中删除特定值时，需要找到该值所在的位置并将其前后的元素连接起来。由于链表保持有序，删除操作可能相对较快。然而，删除操作可能会导致链表长度的变化，从而影响删除操作的运行时间。总体来说，删除操作的运行时间可能会受到一定程度的影响，但具体取决于删除操作的频率和链表的长度。

综上所述，Marley 教授对链模式的改动可能会在不同程度上影响成功查找、不成功查找、插入和删除操作的运行时间。有序链表可以提高查找效率，但插入和删除操作的运行时间可能会受到一定程度的影响。然而，Go 语言的并发支持可以帮助减小这些操作的总体运行时间。在实际应用中，具体的性能提升程度取决于链表的大小、操作的频率以及应用程序的需求。

通义千问：

在 Marley 教授的假设中，将链表保持排序可以改善哈希表的性能。这种方法被称为有序哈希表或者有序链地址法。

对于查找操作，由于链表已经排序，所以可以使用二分查找法来查找元素，这会大大减少查找的时间复杂度，从 O(n) 降低到 O(log n)。

对于不成功的查找，由于链表是有序的，所以在确定没有找到目标元素时，也可以更快地终止查找过程，减少了查找的时间。

对于插入操作，需要先找到应该插入的位置，然后将新元素插入到链表中。由于链表是有序的，因此这个过程可能涉及到一些元素位置的移动，因此插入操作的时间复杂度为 O(n)。

对于删除操作，同样需要先找到要删除元素的位置，然后将其从链表中删除。由于链表是有序的，因此这个过程也可能涉及到一些元素位置的移动，因此删除操作的时间复杂度也为 O(n)。

总的来说，在这种修改之后，查找操作的速度得到了显著提升，而插入和删除操作的速度则受到一定影响。然而，具体的效果还需要根据实际情况进行测试和分析。

天工：

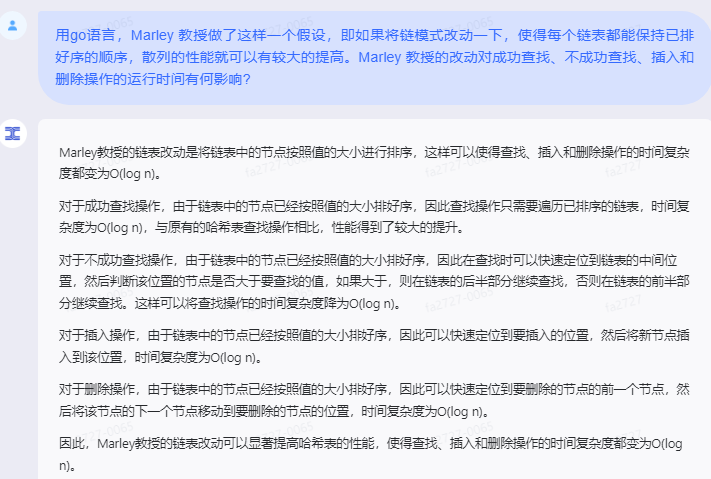
Marley教授的链表改动是将链表中的节点按照值的大小进行排序，这样可以使得查找、插入和删除操作的时间复杂度都变为O(log n)。

对于成功查找操作，由于链表中的节点已经按照值的大小排好序，因此查找操作只需要遍历已排序的链表，时间复杂度为O(log n)，与原有的哈希表查找操作相比，性能得到了较大的提升。

对于不成功查找操作，由于链表中的节点已经按照值的大小排好序，因此在查找时可以快速定位到链表的中间位置，然后判断该位置的节点是否大于要查找的值，如果大于，则在链表的后半部分继续查找，否则在链表的前半部分继续查找。这样可以将查找操作的时间复杂度降为O(log n)。

对于插入操作，由于链表中的节点已经按照值的大小排好序，因此可以快速定位到要插入的位置，然后将新节点插入到该位置，时间复杂度为O(log n)。

对于删除操作，由于链表中的节点已经按照值的大小排好序，因此可以快速定位到要删除的节点的前一个节点，然后将该节点的下一个节点移动到要删除的节点的位置，时间复杂度为O(log n)。

因此，Marley教授的链表改动可以显著提高哈希表的性能，使得查找、插入和删除操作的时间复杂度都变为O(log n)。

灵小智：

根据Marley教授的假设，将链模式改动以保持已排好序的顺序，对各种操作的运行时间会有以下影响：

1.成功查找：由于链表已经按顺序排列，成功查找的运行时间将得到显著提高。在传统链表中，平均情况下需要遍历整个链表才能找到目标元素，而在已排序的链表中，可以使用二分查找等更高效的搜索算法，从而显著减少查找时间。

2.不成功查找：对于不成功的查找，即找不到目标元素的情况，改动后的链表仍然需要遍历整个链表才能确定该元素不存在，所以不成功查找的运行时间不受改动的影响，仍然是线性时间复杂度。

3.插入：由于链表已经排序，插入操作需要找到合适的位置将新元素插入到链表中。相比于传统链表的末尾插入，有序链表的插入需要遵循排序规则，并且可能要移动一些元素的位置，因此插入操作的运行时间会相应增加。

4.删除：与插入类似，删除操作也需要找到目标元素，并将其从链表中移除。由于链表已经按顺序排列，删除操作可能需要遍历一部分链表来找到目标元素，然后再进行删除。因此，删除操作的运行时间可能会有所增加。

总之，将链模式改动以保持已排序的顺序可以提高成功查找的性能，但可能会增加插入和删除操作的运行时间。对于不成功查找，改动后的链表与传统链表的效率相似。

chatgpt：

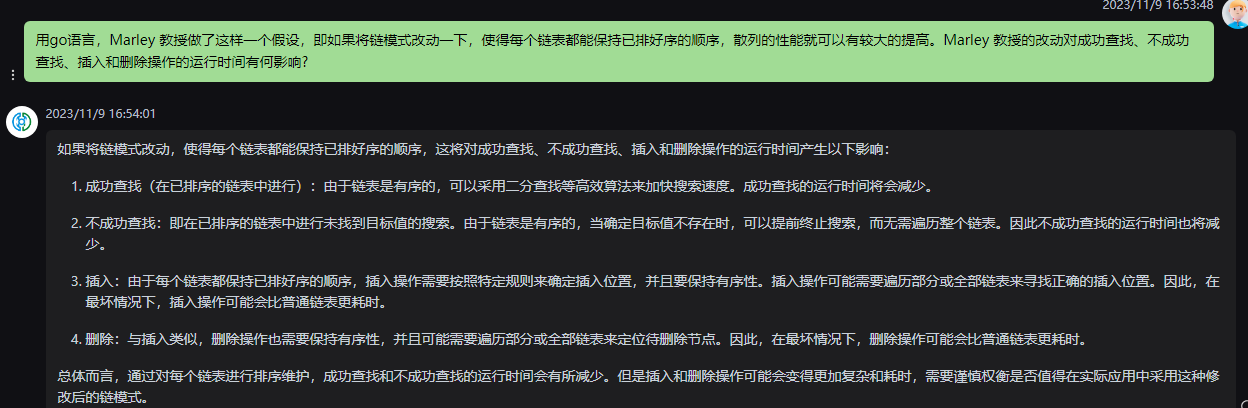
如果将链模式改动，使得每个链表都能保持已排好序的顺序，这将对成功查找、不成功查找、插入和删除操作的运行时间产生以下影响：

1.成功查找（在已排序的链表中进行）：由于链表是有序的，可以采用二分查找等高效算法来加快搜索速度。成功查找的运行时间将会减少。

2.不成功查找：即在已排序的链表中进行未找到目标值的搜索。由于链表是有序的，当确定目标值不存在时，可以提前终止搜索，而无需遍历整个链表。因此不成功查找的运行时间也将减少。

3.插入：由于每个链表都保持已排好序的顺序，插入操作需要按照特定规则来确定插入位置，并且要保持有序性。插入操作可能需要遍历部分或全部链表来寻找正确的插入位置。因此，在最坏情况下，插入操作可能会比普通链表更耗时。

4.删除：与插入类似，删除操作也需要保持有序性，并且可能需要遍历部分或全部链表来定位待删除节点。因此，在最坏情况下，删除操作可能会比普通链表更耗时。

总体而言，通过对每个链表进行排序维护，成功查找和不成功查找的运行时间会有所减少。但是插入和删除操作可能会变得更加复杂和耗时，需要谨慎权衡是否值得在实际应用中采用这种修改后的链模式。