【转载】拒绝遗忘：高效的动态规划算法 —— “到底什么是动态规划”—— An intro to Algorithms: Dynamic Programming

原文地址（英文）：

https://medium.freecodecamp.org/an-intro-to-algorithms-dynamic-programming-dd00873362bb

该文国内有翻译版本：

https://mbd.baidu.com/newspage/data/landingsuper?context=%7B%22nid%22%3A%22news_9735854818841370778%22%7D&n_type=0&p_from=1

PS：本文讲的很通俗易懂，搞计算机十多年了，头一次遇到能把这个问题讲的如此清楚的文章。

-----------------------------------------------------------------------------------------------

英文原版：

Suppose you are doing some calculation using an appropriate series of input. There is some computation done at every instance to derive some result. You don’t know that you had encountered the same output when you had supplied the same input. So it’s like you are doing re-computation of a result that was previously achieved by specific input for its respective output.

But what’s the problem here? Thing is that your precious time is wasted. You can easily solve the problem here by keeping records that map previously computed results. Such as using the appropriate data structure. For example, you could store input as key and output as a value (part of mapping).

Those who cannot remember the past are condemned to repeat it. 
                                             ~Dynamic Programming

Now by analyzing the problem, store its input if it’s new (or not in the data structure) with its respective output. Else check that input key and get the resultant output from its value. That way when you do some computation and check if that input existed in that data structure, you can directly get the result. Thus we can relate this approach to dynamic programming techniques.

Diving into dynamic programming

In a nutshell, we can say that dynamic programming is used primarily for optimizing problems, where we wish to find the “best” way of doing something.

A certain scenario is like there are re-occurring subproblems which in turn have their own smaller subproblems. Instead of trying to solve those re-appearing subproblems, again and again, dynamic programming suggests solving each of the smaller subproblems only once. Then you record the results in a table from which a solution to the original problem can be obtained.

For instance, the Fibonacci numbers 0,1,1,2,3,5,8,13,… have a simple description where each term is related to the two terms before it. If F(n) is the nth term of this series then we have F(n) = F(n-1) + F(n-2). This is called a recursive formula or a recurrence relation. It needs earlier terms to have been computed in order to compute a later term.

The majority of Dynamic Programming problems can be categorized into two types:

Optimization problems.
Combinatorial problems.

The optimization problems expect you to select a feasible solution so that the value of the required function is minimized or maximized. Combinatorial problems expect you to figure out the number of ways to do something or the probability of some event happening.

An approach to solve: top-down vs bottom-up

There are the following two main different ways to solve the problem:

Top-down: You start from the top, solving the problem by breaking it down. If you see that the problem has been solved already, then just return the saved answer. This is referred to as Memoization.

Bottom-up: You directly start solving the smaller subproblems making your way to the top to derive the final solution of that one big problem. In this process, it is guaranteed that the subproblems are solved before solving the problem. This can be called Tabulation (table-filling algorithm).

In reference to iteration vs recursion, bottom-up uses iteration and the top-down uses recursion.

The visualization displayed in the image is not correct acc. to theoretical knowledge, but I have displayed in an understandable manner

Here there is a comparison between a naive approach vs a DP approach. You can see the difference by the time complexity of both.

Memoization: Don’t forget

Jeff Erickson describes in his notes, for Fibonacci numbers:

The obvious reason for the recursive algorithm’s lack of speed is that it computes the same Fibonacci numbers over and over and over.

From Jeff Erickson’s notes CC: http://jeffe.cs.illinois.edu/

We can speed up our recursive algorithm considerably just by writing down the results of our recursive calls. Then we can look them up again if we need them later.

Memoization refers to the technique of caching and reusing previously computed results.

If you use memoization to solve the problem, you do it by maintaining a map of already solved subproblems (as we earlier talked about the mapping of key and value). You do it “top-down” in the sense that you solve the “top” problem first (which typically recurses down to solve the sub-problems).

Pseudocode for memoization:

So using recursion, we perform this with extra overhead memory (i.e. here lookup) to store results. If there is a value stored in the lookup, we return it directly or we add it to lookup for that specific index.

Remember that there is a tradeoff of extra overhead with respect to the tabulation method.

However, if you want more visualizations for memoization, then I suggest looking into this video.

In a top-down manner.

Tabulation: Filling up in tabular form

But once we see how the array (memoized solution) is filled, we can replace the recursion with a simple loop that intentionally fills the array in order, instead of relying on the complicated recursion to do it for us ‘accidentally’.

From Jeff Erickson’s notes CC: http://jeffe.cs.illinois.edu/

Tabulation does it in “bottom-up” fashion. It’s more straight forward, it does compute all values. It requires less overhead as it does not have to maintain mapping and stores data in tabular form for each value. It may also compute unnecessary values. This can be used if all you want is to compute all values for your problem.

Pseudocode for tabulation:

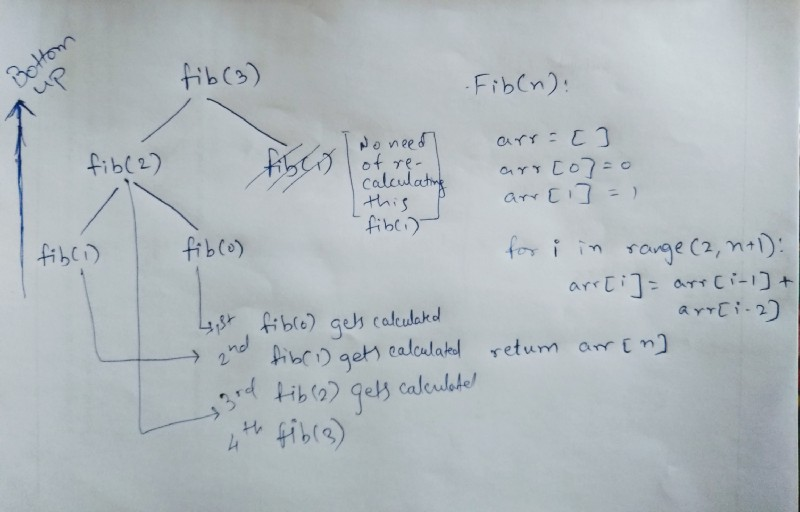
Pseudocode with Fibonacci tree

As you can see pseudocode (right side) in an image, it does iteration (i.e. loops over till the end of an array). It simply starts with fib(0),fib(1),fib(2),… So with the tabulation approach, we can eliminate the need for recursion and simply return the result with looping over elements.

Looking back in history

Richard bellman was the man behind this concept. He came up with this when he was working for RAND Corporation in the mid-1950s. The reason he chose this name “dynamic programming” was to hide the mathematics work he did for this research. He was afraid his bosses would oppose or dislike any kind of mathematical research.

Okay, so the word ‘programming’ is just a reference to clarify that this was an old-fashioned way of planning or scheduling, typically by filling in a table (in a dynamic manner rather than in a linear way) over the time rather than all at once.

Wrapping up

That’s it. This is part 2 of the algorithm series I started last year. In my previous post, we discussed about what are searching and sorting algorithms. Apologies that I couldn’t deliver this in a shorter time. But I am willing to make things faster in the coming months.

Hope you liked it and I’ll be soon looking to add a third one in the series soon. Happy coding!

Resources:

Introduction to Dynamic Programming 1 Tutorials & Notes | Algorithms | HackerEarth
The image above says a lot about Dynamic Programming. So, is repeating the things for which you already have the…www.hackerearth.com Community — Competitive Programming — Competitive Programming Tutorials — Dynamic Programming: From…
Community — Competitive Programming — Competitive Programming Tutorials — Dynamic Programming: From Novice to Advancedwww.topcoder.com

https://www.geeksforgeeks.org/overlapping-subproblems-property-in-dynamic-programming-dp-1/

Special props to Jeff Erickson and his notes for algorithm — http://jeffe.cs.illinois.edu/

---------------------------------------------------------------------------------------------

中文翻译版：

https://mbd.baidu.com/newspage/data/landingsuper?context=%7B%22nid%22%3A%22news_9735854818841370778%22%7D&n_type=0&p_from=1

*tabulation*的伪代码：

-----------------------------------------------------------------------------------------------