DP_最长公共子序列/动规入门

学自：https://open.163.com/movie/2010/12/L/4/M6UTT5U0I_M6V2U1HL4.html

最长公共子序列：（本文先谈如何求出最长公共子序列的长度，求出最长公共子序列在文章最下方）

　　昨天看了网易公开课的麻省理工的算法导论讲的最长公共子序列，收获很大，网址已给出，推荐观看。我也将会把如何减少算法的空间的代码放在下面，这是视频中提到的，用的也是老师所说的保存一行，好，现在来说说最长公共子序列的求法。先把问题简单描述一下，就是有两个字符串序列，求他们最长的公共子序列，所谓公共子序列，就是两个字符串序列所共有的序列，可以不是连在一起的，如：x:ABCDEFGHI y:AZBZCZDZEZF 那他们的最长公共子序列就是ABCDEF,他们的所有的公共子序列是这个最长公共子序列的所有子集。可以看出，公共子序列中每个元素的相对应的前后位置在两个原有序列中相同的元素的对应的前后位置是一样的，就如在公共子序列中B在A后面，在两个原序列中都是B在A后面，但B和A可以不相连。

　　那么如何来求这个序列呢，首先想到的穷举法就是暴力的求解，就是把x中所有的子序列全列出来，然后在y中找是否有相同的子序列，再在相同中找出最大的，那么这个算法复杂度是多少，先看x中的子序列一共有多少个，如果x的长度为m，则它的自序列就有2^m个，假设y的长度为m，则对于每个x的子序列，都得在y中判断一次，看是不是y的子序列，那么每个x的子序列都要花费n的时间来遍历y，所以整个算法的时间复杂度是O(n*2^m)，这个时间复杂度是指数级的，用一个词来描述次算法就是龟速。但穷举法在某些情况下还是挺好用的，所以在想不出来更好的算法时候，不妨考虑考虑穷举法。

　　更好一点算法就是，我们定义c[i,j]来记录x和y的LCS长度，c[i,j] = |LCS(X[1,i],y[1,j])|（注意这个加个绝对值号代表长度，没加绝对值号代表这序列 也就是字符串） 那么c[m,n]就是x和y的最长公共子序列的长度,那么现在就是算出c[m,n]，现在需要c[i,j]的推导式，然后在求出c[m,n]；c[i,j]的推导式：

　　　　　　c[i-1,j-1]+1, if x[i]=y[j];

c[i,j] =

　　　　　　max{ c[i,j-1],c[i-1,j] }, x[i] != y[j];

这就是c[i,j]的推导公式，很明显是个递归式 。下面来证明这个公式，先看一张图：

定义z[1,k] = LCS(x[1,i],y[1,j]);当c[i,j] = k时，z[k] = x[i]( = y[j])因为此时x[i]和y[j]是相等的，如果z[k]里面没有包含x[i]或者说y[j]这个字符，那我们就把x[i]这个字符加上。那么z[k-1]就是序列x[1,i-1]和序列y[1,j-1]的最长公共子序列。下面我们来证明这个命题:

　　假设w是一个更长的公共子序列，也就是说w的长度要大于k-1（|w| > k-1），也就是说，如果存在一个公共子序列的长度比z[1,k-1]长，那么这个子序列的长度就要大于k-1。这样，如果我们把w拿出来，把最后的字符z[k]连接在后面，把它们连接在一起，那么连接后的子序列就是x[1,i]和y[1,j]的一个公共子序列,它的长度一定大于k，因为w的长度已经比k-1大了，现在我们把后面又加了一个字符，那么新序列的长度一定比k大，这就矛盾，所以假设不成立，也就是没有一个更长的公共子序列了，也就是说z[k-1]就是x[1,i-1],y[1,j-1]的最长公共子序列，那么序列z[1,k-1]+上x[i]这个字符就是z[1,k]这个序列就是x[1,i] 和 y[1,j] 的最长公共子序列，定义得证。由上可得c[i-1,j-1]的长度就是k-1，那说明c[1,j] = c[i-1,j-1] + 1;

其实上面讲的就是动态规划的第一个特征，下面说动态规划的特征，第一条这也是最优子结构的性质，意思是问题(计算机中的问题就是有很多实例)的一个最优解包含了子问题的最优解。例如，z = LCS(x,y)，那么任何z的前缀都是某个x的前缀和某个y的前缀的LCS。当我拿到这个问题是，我发现了里面存在着最优子结构，在这种结构下，你总能用上面的方法来证明，证明如果子问题的解不是最优的，那么用哪种方法你总能找到一个全局最优解。

动态规划的第二个特征就是：重叠子问题。如果在一个递归的过程，也可以说是在求解一个问题的过程中，包含了独立的子问题被反复计算了多次。此时应用备忘法来记录下子问题的解，做备忘的意思就是我已经算完了，如果需要这个值的时候，拿来用就行了。所以对于上面的最长公共子序列问题，将问题所有的子问题的解做成一个表就行了，例如：x:ACBCD,y:CABDCD看下图：

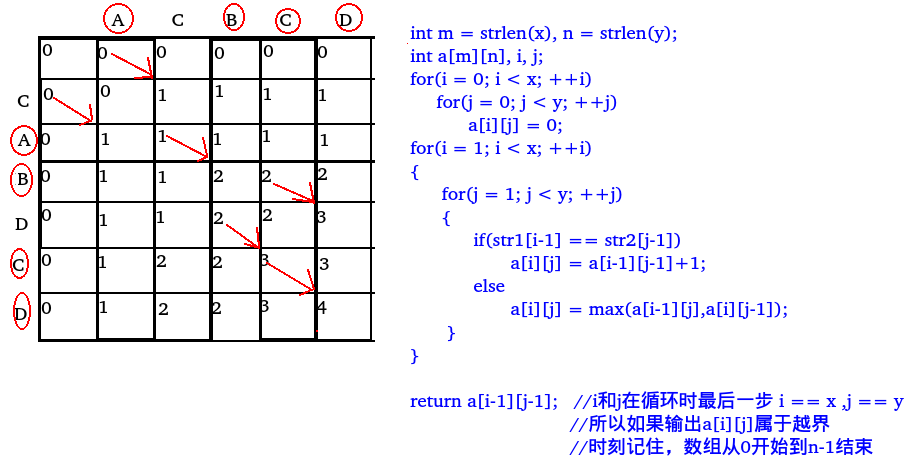
这样下来返回的就是最长公共子序列的长度，现在我们考虑如何节省空间，扩展思维，我们再算每一行的时候，只需要上一行的数据，所以我们只需要保存一行的数据就可以了；下面是我的代码

/*************************************************************
 * > File Name: LSC省空间算法.cpp
 * > Author: weigang
 * > Mail: w_wg@qq.com
 * > Created Time: 2018年05月20日 星期日 21时14分03秒
 *************************************************************/

/* 何为省空间算法，指的是在存储表的时候，使得空间最少，即为
 * 两个字符串序列的最短的那个*/

#include<bits/stdc++.h>
using namespace std;//原算法
//这个算法如果让你求出最长公共子序列是什么 就可以改进一下就行
//因为每次结果都保留了运算结果
int LCS(string str1,string str2)
{
    int x = str1.size()+,y = str2.size()+;
    int a[x][y],i,j;
    for(i = ; i < x; ++i)
        for(j = ; j < y; ++j)
            a[i][j] = ;
    for(i = ; i < x; ++i)
    {
        for(j = ; j < y; ++j)
        {
            if(str1[i-] == str2[j-])
                a[i][j] = a[i-][j-]+;
            else
                a[i][j] = max(a[i-][j],a[i][j-]);
        }
    }return a[i-][j-];//i和j在循环时最后一步 i == x ,j == y
                        //所以如果输出a[i][j]属于越界
                        //时刻记住，数组从0开始到n-1结束
}
//改进算法，降低空间利用，原算法空间m*n 新算法min{m,n}
//在上面计算时候我们就可以看到 我其实只要上面一行就可以求出这
//一行的数据，所以每次我们可以值保存一行的数据 就可以求出答案
int LCS_puls(string str1,string str2)
{
    int x = str1.size()+,y = str2.size()+;
    int a[x],i,j,t;
    for(i = ; i < x; ++i)
        a[i] = ;
    for( i = ; i < y; ++i )
    {
        for( j = ; j < x; ++j )
        {
            t = a[j-];
            if( str2[i-] == str1[j-] )
                a[j] = t + ;
            else
                a[j] = max( a[j],t );
        }
    }

    return a[j-];
}
int main(void)
{
    string str1,str2;
    cin >> str1 >> str2;
    /* 原算法 */
    cout << LCS(str1,str2) << endl;
    /* 改进算法
    if( str1.size() > str2.size() )
    {
        string t = str1;
        str1 = str2;
        str2 = t;
    }
    cout << LCS_puls(str1,str2) << endl;*/

    return ;
}

---

如果想求出最长公共子序列，在求最长公共子序列的基础上，有两种方法来求，试想，我们在求得最长公共子序列的长度时有一递推公式，我们只需要将递推公式反着来即可求出最长的公共子序列，第二种方法就是在求最长公共子序列的长度的同时，将d[i][j]如何求的给记录下来，然后再从最下面走回去即可。具体代码实现如下。

/* 建立一个二维数组用来记录求得最长子序列的路径
#include<bits/stdc++.h>
using namespace std;

int dp[1005][1005],s[1005][1005];

int main(void)
{
    string a,b;
    cin >> a >> b;
    int len_a = a.size(), len_b = b.size();
    for(int i = 1; i <= len_a; ++i) {
        for(int j = 1; j <= len_b; ++j) {
            if( a[i-1] == b[j-1]) {
                dp[i][j] = dp[i-1][j-1] + 1;
                s[i][j] = 1;
             } else {
                if( dp[i-1][j] >= dp[i][j-1] ) {
                    dp[i][j] = dp[i-1][j];
                    s[i][j] = 2;
                } else {
                    dp[i][j] = dp[i][j-1];
                    s[i][j] = 3;
                }
            }
        }
    }
    char ch[dp[len_a][len_b]];
    int k = 0;
    for(int i = len_a,j = len_b; i > 0 && j > 0; ) {
        switch( s[i][j] ) {
            case 1:
                ch[k] =  a[i-1]; --i; --j; k++; break;
            case 2:
                --i; break;
            case 3:
                --j;
        }
    }
    for(int i = k-1; i >= 0; --i) {
        cout << ch[i];
    }
    cout << endl;

    return 0;
} */

// 利用回溯法求最长公共子序列
#include<bits/stdc++.h>
using namespace std;

int dp[][];
char tch[];
string a,b;

int main(void)
{
    cin >> a >> b;

    int len_a = a.size();
    int len_b = b.size();

    for(int i = ; i <= len_a; ++i) {
        for(int j = ; j <= len_b; ++j) {
            if( a[i-] == b[j-] ) {
                dp[i][j] = dp[i-][j-] + ;
            } else {
                dp[i][j] = max(dp[i-][j], dp[i][j-]);
            }
        }
    }

    int k = dp[len_a][len_b];
    for( int i = len_a, j = len_b; i >  && j > ; ) {  // 回溯
        if( a[i-] == b[j-] && dp[i][j] == dp[i-][j-]+  ) {
            tch[--k] = a[i-];
            i--;j--;
        } else if( a[i-] != b[j-] && dp[i-][j] > dp[i][j-] ) i--;
        else j--;
    }

    printf("%s",tch);

    return ;
}