BOOTH 算法的简单理解

学习FPGA时，对于乘法的运算，尤其是对于有符号的乘法运算，也许最熟悉不过的就是 BOOTH算法了。

这里讲解一下BOOTH算法的计算过程，方便大家对BOOTH的理解。

       上图是BOOTH算法的数学表达。由于FPGA擅长进行并行移位计算，所以BOOTH算法倒也好实现。

上图是对乘数的加码过程，具体可以见下面的例子。

7 x （-3），其中R1表示被乘数 7， R2 表示乘数 -3，那么二者对应的补码，为 R1 0111，R2 1101，

P代码最终结果容量，应该为 2x 4 + 1 = 9位，其中一位作为辅助位。计算过程如下：

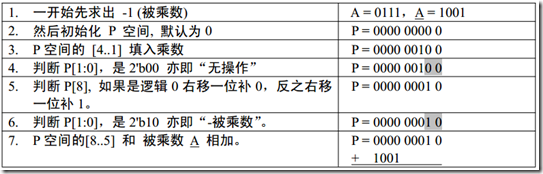
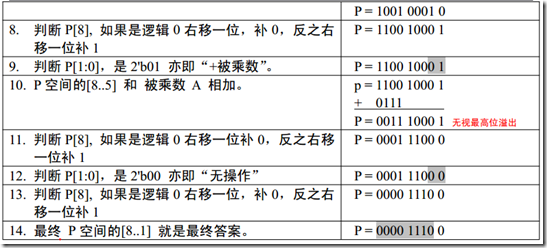
上述的计算过程需要注意，在进行右移时，需要将P = {R0，R2}，当作整体看待，若P[8]最高位为0，则

移位之后的结果R0的最高位就补0，若是1就补1，由上图的第7步到第8步的变换，{R0，R2} =

{1001，,0001}，那么P的最高位是1，则以后之后，R0的高位需要补1，所以得到移位之后的结果{R0，R2} =

{1100,1000}，并且辅助位由于乘数的低位是1，所以辅助位为1，辅助位和乘数的移调的位的逻辑值有关，比

如乘数是0010，则四次操作的辅助为 0， 1， 0， 0。