BiliBili, ACFun… And More!【递归算法】

题源：http://acm.uestc.edu.cn/#/problem/show/3

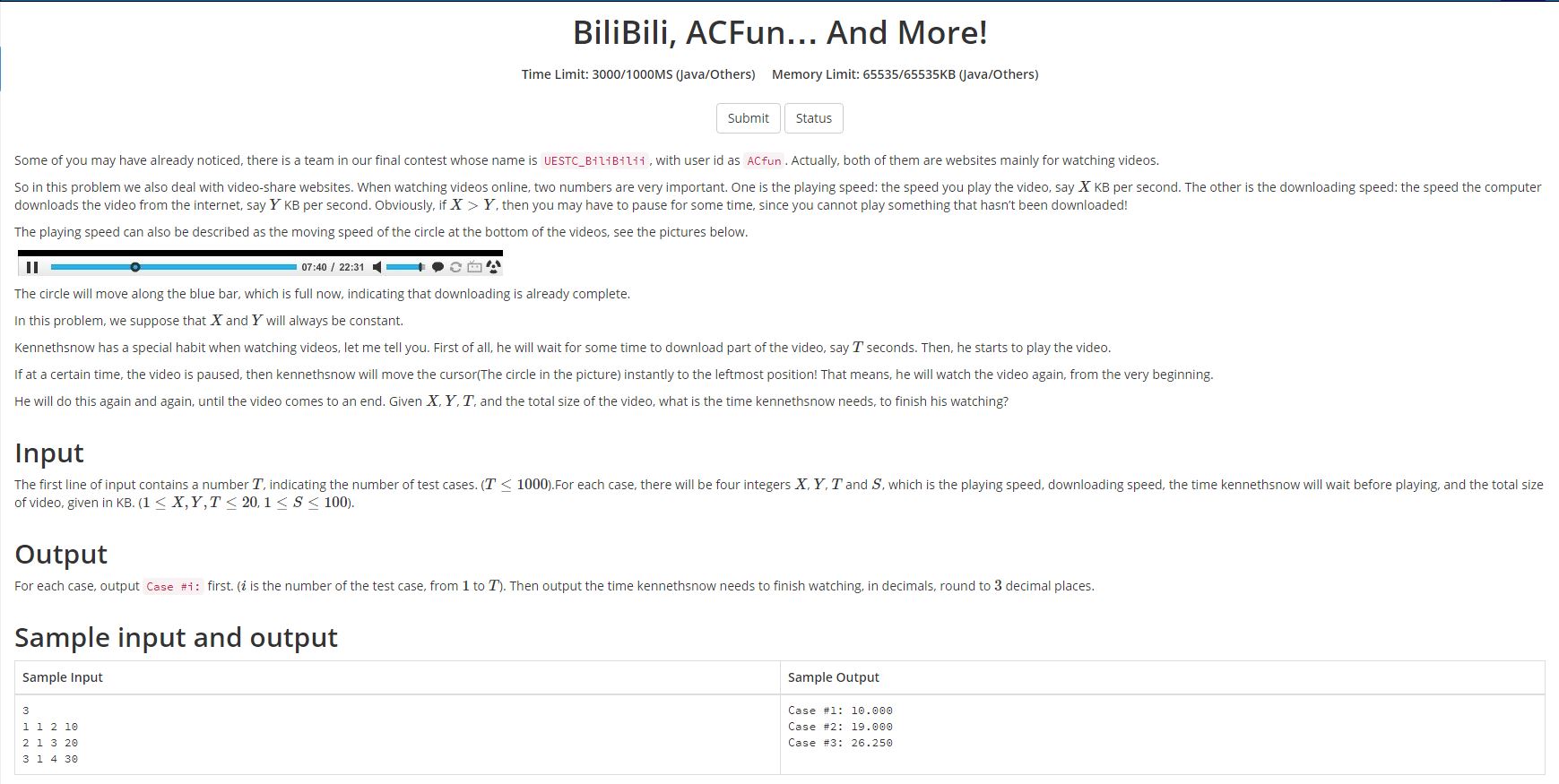
题解：

　　题意：播放一段视频文件，有播放速度和缓冲速度两种，因为作者的癖好，播放前要缓冲几秒钟(这段时间不计算在总时间内)，如果当播放文件大小等于缓冲文件大小时，缓冲文件还没有缓冲完，播放器会从头开始，但缓冲继续缓冲。

　　总结几个关键点：

　　　　1.当需要重新播放的时候，已经缓冲的大小（这里的性质等于开始播放前缓冲的大小），此时的情形类似最开始的情况，只是提前缓冲大小不一样了。

　　　　2.当播放大小等于缓冲大小（这里列一个方程），判断缓冲大小是否大于等于总大小，否则重新播放。

　　根据关键点的信息，可以嗅出递归算法的味道，什么是递归算法？

　　在数学中，递归是X0属于A集合，f(X0) = f(f(X1))，X0等于在X1对应的因变量。外层需要内层运算的结果

　　在编程中，递归是函数自己调用自己，但有一个递归出口。函数调用实际上是在“栈”中进行，最先调用的函数在栈底。

　　网上扣一张图能很形象理解递归（如有侵权立即删除）

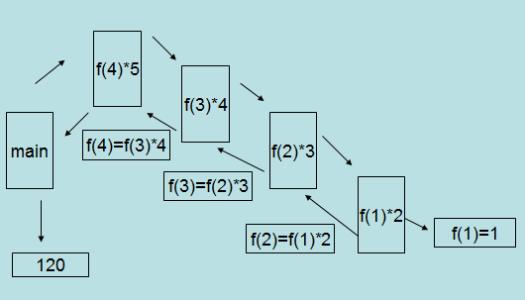
回归正题：

设播放速度为X，缓冲速度为Y，提前播放的时间T，文件总大小Z，需要的时间t，重新播放前一刻的缓冲大小Size。

1.分两种情况。

　　1）网速倍儿棒，一次都没重新播放过

　　　　t = Z/X

　　　　满足条件：缓冲速度Y大于等于播放速度X   或者   当要重新播放的时候，缓冲大小大于总大小

　　　　　　　　　Y >= X  ||  T/(X - Y) >= S/X

　　2）令人抓狂的情况，老是重新播放

　　　　t = t1 + t2 + t3 ... + tn;

　　　　tn = Size/(X-Y);//第N次递归的播放时间

　　　　递归相同式子：缓冲文件大小Size，调用自身函数时，缓冲文件大小变为Size/(X-Y)*X;

　　　　递归终止条件：缓冲文件大小大于等于总文件大小S：size / (X - Y)*X >= S

附上代码：

//C code

#include<stdio.h>

#define M 1000

double Time(double size, int X, int Y, int S);//递归函数

int main()
{
	int num,X[M],Y[M],S[M],T[M];//X playspeed播放速度,Y bufferspeed缓冲速度,S totalsize文件总大小
	int i;//循环参数
	scanf("%d", &num);//测试数目
	for (i = 0; i < num; i++)
	{
		scanf("%d %d %d %d", &X[i], &Y[i],&T[i], &S[i]);
	}
	for (i = 0; i < num; i++)
	{
		if (X[i] <= Y[i] || T[i] / (double)(X[i] - Y[i]) >= S[i] / (double)X[i])//网速好
		{
			printf("Case #%d: %.3f\n", i+1, S[i] / (double)X[i]);
		}
		else//辣鸡网速
		{
			printf("Case #%d: %.3f\n", i + 1, Time(T[i] * Y[i], X[i], Y[i], S[i]));
		}
	}
    return 0;
}

double Time(double size,int X,int Y,int S)//size是重新播放前一刻的缓冲文件大小，作为递归变量
{
	double t = 0;
	if (size / (X - Y)*X < S)//递归终止条件
	{
		t = size / (X - Y) + Time(size / (X - Y)*X, X, Y, S);
	}
	else
	{
		t = S / (double)X;
	}
	return t;
}

　　

有什么问题欢迎在留言区交流！