P2668 斗地主

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的AAA到KKK加上大小王的共545454张牌来进行的扑克牌游戏。在斗地主中，牌的大小关 系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王3<4<5<6<7<8<9<10<J<Q<K<A<2<\text{小王}<\text{大王}3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由 nnn 张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。具体规则如下：

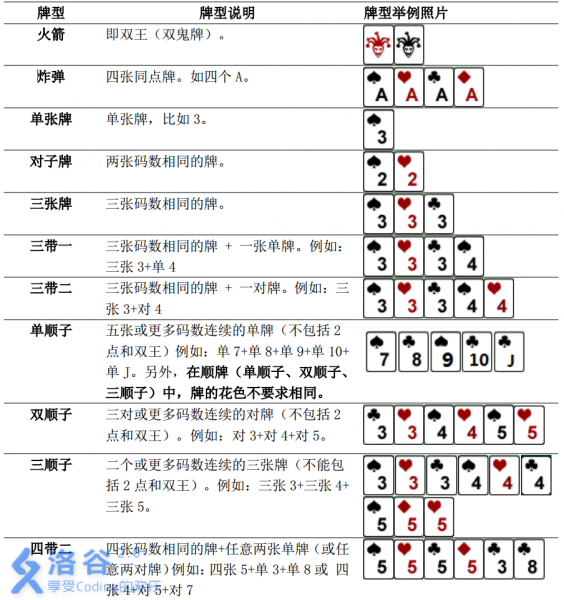
本题数据随机，不支持hack，要hack或强力数据请点击这里

输入输出格式

输入格式：

第一行包含用空格隔开的2个正整数 T,nT,nT,n ，表示手牌的组数以及每组手牌的张数。

接下来 TTT 组数据，每组数据 nnn 行，每行一个非负整数对 ai,bia_i,b_iai​,bi​ ，表示一张牌，其中 aia_iai​ 表示牌的数码， bib_ibi​ 表示牌的花色，中间用空格隔开。特别的，我们用 111 来表示数码 AAA， 111111 表示数码J JJ， 121212 表示数码Q QQ， 131313 表示数码 KKK；黑桃、红心、梅花、方片分别用 1−41-41−4 来表示；小王的表示方法为 010101 ，大王的表示方法为 020202 。

输出格式：

共 TTT 行，每行一个整数，表示打光第 iii 组手牌的最少次数。

输入输出样例

输入样例#1： 复制

1 8

7 4

8 4

9 1

10 4

11 1

5 1

1 4

1 1

输出样例#1： 复制

3

输入样例#2： 复制

1 17

12 3

4 3

2 3

5 4

10 2

3 3

12 2

0 1

1 3

10 1

6 2

12 1

11 3

5 2

12 4

2 2

7 2

输出样例#2： 复制

6

说明

样例1说明

共有111组手牌，包含8张牌：方片777，方片888，黑桃999，方片101010，黑桃JJJ，黑桃555，方片AAA以及黑桃AAA。可以通过打单顺子（方片777，方片888，黑桃999，方片101010，黑桃JJJ），单张牌（黑桃555）以及对子牌（黑桃AAA以及方片AAA）在333次内打光。

对于不同的测试点， 我们约定手牌组数TTT与张数nnn的规模如下：

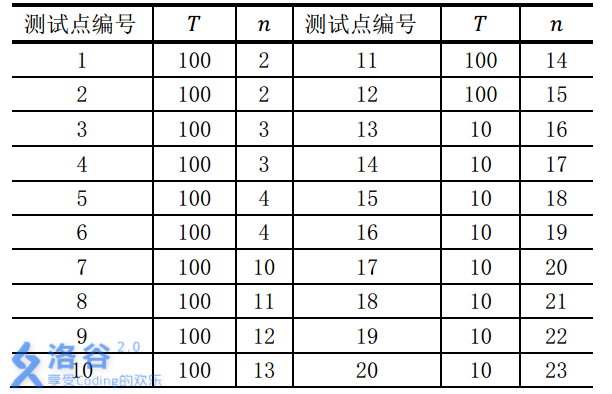
数据保证：所有的手牌都是随机生成的。

---

其实只需要一个剪枝，在暴力穷举完不定长的出法之后按照从多到少的顺序枚举定长的出法，每次枚举前判断如多剩余卡牌数除以当前状态最多一次出牌数大于当前最佳答案直接\(return\)

我的第一个行数\(200+\)的代码<(￣︶￣)>

---

#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;

int i,m,n,j,k,a[101],t,g,h,ans=0x3f3f3f3f;

void dfs(int k,int *d,int res,int num)
{
    if(num==1)
    for(int i=3;i<=13;i++)
    {
        if((d[i]<3)||(d[i+1]<3)) continue;
        d[i]-=3; res-=3;
        int t=1;
        while(d[i+t]>=3)
        {
            d[i+t]-=3;
            res-=3;
            dfs(k+1,d,res,1);
            t+=1;
        }
        while(t--)	d[t+i]+=3,res+=3;
    }
    if(num==1)
    for(int i=3;i<=12;i++)
    {
        if((d[i]<2)||(d[i+1]<2)||(d[i+2]<2)) continue;
        d[i]-=2; d[i+1]-=2; res-=4;
        int t=2;
        while(d[i+t]>=2)
        {
            d[i+t]-=2;
            res-=2;
            dfs(k+1,d,res,1);
            t+=1;
        }
        while(t--) d[t+i]+=2,res+=2;
    }
    if(num==1)
    for(int i=3;i<=10;i++)
    {
        if((!d[i])||(!d[i+1])||(!d[i+2])||(!d[i+3])||(!d[i+4])) continue;
        d[i]-=1; d[i+1]-=1; d[i+2]-=1; d[i+3]-=1;	res-=4;
        int t=4;

        while(d[i+t])
        {
            d[i+t]-=1;
            res-=1;
            dfs(k+1,d,res,1);
            t+=1;
        }
        while(t--)
            d[i+t]+=1,res+=1;
    }

    if(res/8+k>=ans) return;
    for(int i=3;i<=16;i++)
    {
        if(d[i]<4) continue;
        d[i]-=4;
        res-=4;
        for(int j=3;j<=16;j++)
            if(d[j]>=2)
            for(int l=j;l<=16;l++)
                if(((j==l)&&(d[l]>=4))||((j!=l)&&(d[l]>=2)))
                {
                    d[l]-=2; d[j]-=2; res-=4;
                    dfs(k+1,d,res,0);
                    d[l]+=2; d[j]+=2; res+=4;
                }
        res+=4;
        d[i]+=4;
    }

    if(res/6+k>=ans) return;
    for(int i=3;i<=16;i++)
    {
        if(d[i]<4) continue;
        d[i]-=4; res-=4;
        for(int j=3;j<=17;j++)
            if(d[j])
            for(int l=j;l<=17;l++)
                if(((j==l)&&(d[l]>=2))||((j!=l)&&(d[l])))
                {
                    d[l]-=1; d[j]-=1; res-=2;
                    dfs(k+1,d,res,0);
                    d[l]+=1; d[j]+=1; res+=2;
                }
        res+=4; d[i]+=4;
    }

    if(res/5+k>=ans) return;
    for(int i=3;i<=16;i++)
    {
        if(d[i]<3) continue;
        d[i]-=3; res-=3;
        for(int j=3;j<=16;j++)
            if(d[j]>1)
            {
                d[j]-=2; res-=2;
                dfs(k+1,d,res,0);
                d[j]+=2; res+=2;
            }
        res+=3;	d[i]+=3;
    }

    if(res/4+k>=ans) return;
    for(int i=3;i<=16;i++)
    {
        if(d[i]<3) continue;
        d[i]-=3; res-=3;
        for(int j=3;j<=17;j++)
            if(d[j])
            {
                d[j]-=1; res-=1;
                dfs(k+1,d,res,0);
                d[j]+=1; res+=1;
            }
        res+=3;	d[i]+=3;
    }

    if(res/3+k>=ans) return;
    for(int i=3;i<=16;i++)
    {
        if(d[i]<3) continue;
        d[i]-=3; res-=3;
        dfs(k+1,d,res,0);
        res+=3;	d[i]+=3;
    }

    if(res/2+k>=ans) return;
    for(int i=3;i<=17;i++)
    {
        if(d[i]<2) continue;
        d[i]-=2; res-=2;
        dfs(k+1,d,res,0);
        res+=2;	d[i]+=2;
    }

    ans=min(ans,k+res);

}

int main()
{
    scanf("%d%d",&t,&n);
    for(t;t>=1;t--)
    {
        memset(a,0,sizeof(a));
        ans=0x3f3f3f3f;
        for(i=1;i<=n;i++)
        {
            scanf("%d%d",&g,&h);
            if(g==0) a[17]+=1;
            else if(g==2) a[16]+=1;
            else if(g==1) a[14]+=1;
            else a[g]+=1;
        }
        dfs(0,a,n,1);
        printf("%d\n",ans);
    }

}

加强版会被hack掉一个点T到爆炸...QAQ