数论——扩展的欧几里德算法 - HDU2669
http://acm.hdu.edu.cn/showproblem.php?pid=2669
#include <iostream>
using namespace std;
int gcd(int a, int b, int &x, int &y) {
) {
x = , y = ;
return a;
}
int q = gcd(b, a%b, y, x);
y -= a / b * x;
return q;
}
int main() {
int a, b;
while (scanf("%d%d", &a, &b) != EOF) {
int x, y;
)
cout << "sorry" << endl;
else {
) {
x += b; y -= a;
}
cout << x << " " << y << endl;
}
}
;
}

这里的x2,y2是递归返回阶段,上一层的y和x,所以代码中的是y-=a/b*x。以21/8为示例,返回阶段递归示意图。

题目要求X必需为非负数,最后这个是很容易忽略掉的,很好看懂,但是写题目的时候没有想到可以这样写。
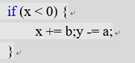

数论——扩展的欧几里德算法 - HDU2669的更多相关文章
- ACM数论之旅4---扩展欧几里德算法(欧几里德(・∀・)?是谁?)
为什么老是碰上 扩展欧几里德算法 ( •̀∀•́ )最讨厌数论了 看来是时候学一学了 度娘百科说: 首先, ax+by = gcd(a, b) 这个公式肯定有解 (( •̀∀•́ )她说根据数论中的相 ...
- (扩展欧几里德算法)zzuoj 10402: C.机器人
10402: C.机器人 Description Dr. Kong 设计的机器人卡尔非常活泼,既能原地蹦,又能跳远.由于受软硬件设计所限,机器人卡尔只能定点跳远.若机器人站在(X,Y)位置,它可以原地 ...
- 欧几里德与扩展欧几里德算法 Extended Euclidean algorithm
欧几里德算法 欧几里德算法又称辗转相除法,用于计算两个整数a,b的最大公约数. 基本算法:设a=qb+r,其中a,b,q,r都是整数,则gcd(a,b)=gcd(b,r),即gcd(a,b)=gcd( ...
- poj2142-The Balance(扩展欧几里德算法)
一,题意: 有两个类型的砝码,质量分别为a,b;现在要求称出质量为d的物品, 要用多少a砝码(x)和多少b砝码(y),使得(x+y)最小.(注意:砝码位置有左右之分). 二,思路: 1,砝码有左右位置 ...
- poj2115-C Looooops(扩展欧几里德算法)
本题和poj1061青蛙问题同属一类,都运用到扩展欧几里德算法,可以参考poj1061,解题思路步骤基本都一样.一,题意: 对于for(i=A ; i!=B ;i+=C)循环语句,问在k位存储系统中循 ...
- poj1061-青蛙的约会(扩展欧几里德算法)
一,题意: 两个青蛙在赤道上跳跃,走环路.起始位置分别为x,y. 每次跳跃距离分别为m,n.赤道长度为L.两青蛙跳跃方向与次数相同的情况下, 问两青蛙是否有方法跳跃到同一点.输出最少跳跃次数.二,思路 ...
- HDU 1576 A/B 扩展欧几里德算法
A/B Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submis ...
- 欧几里德算法及其扩展(推导&&模板)
有关欧几里德算法整理: 1.一些相关概念: <1>.整除性与约数: ①一个整数可以被另外一个整数整除即为d|a(表示d整除a,通俗的说是a可以被d整除),其含义也可以说成,存在某个整数k, ...
- ACM_扩展欧几里德算法
<pre name="code" class="cpp">/* 扩展欧几里德算法 基本算法:对于不完全为 0 的非负整数 a,b,gcd(a,b)表 ...
随机推荐
- JavaScript中自定义函数以及文本框、radio、下拉框的值的获取,结合淘宝竞拍案例来理解。。。
淘宝竞拍案例: HTML部分代码: <form action="#" method="post"> <h2>欢迎进入淘宝竞拍</h ...
- [转]C# 6.0 的新特性
本文的内容包括引入C#6.0中的新的语言特性有哪些. 还有已经被引入的代码名称为 “Roslyn”新编译器. 编译器是开放源码的,并且可以从 codeplex 网站的这个地址下载到源代码: https ...
- ASP.NET页面支持的指令
页面的处理指令 页面指令的处理用于配置执行该页面的运行时环境.在ASP.NET中,指令可以位于页面的任何位置,但良好且常见的习惯是将其置于文件的开始部分.除此,页面指令的名称是不区分大小写的,且指令的 ...
- js 判断浏览器是否64位
js判断是否64位 浏览器 navigator.userAgent.match(/x64/i);
- poj 2417 Discrete Logging ---高次同余第一种类型。babystep_gaint_step
Discrete Logging Time Limit: 5000MS Memory Limit: 65536K Total Submissions: 2831 Accepted: 1391 ...
- Java 并发:Executor
异常捕获 以前使用executor的时候,为了记录任务线程的异常退出会使用ThreadFactory来设置线程的UncaughtExceptionHandler,但是按照书上的验证发现,采用execu ...
- js-script标签放在的位置
* 建议把script标签放到</body>后面 * 如果现在有这样一个需求 在js里面需要获取到input里面的值,如果把script标签放到head里面,会出现问题.HTML解析是从上 ...
- BZOJ4513: [Sdoi2016]储能表(数位dp)
题意 题目链接 Sol 一点思路都没有,只会暴力,没想到标算是数位dp??Orz 首先答案可以分成两部分来统计 设 \[ f_{i,j}= \begin{aligned} i\oplus j & ...
- bootstrap Table的使用方法
1.官网 url:http://bootstrap-table.wenzhixin.net.cn/zh-cn/documentation/ 文档包含了表格属性.列属性.事件.方法等等. 2.引入库 只 ...
- C# 将html文本转化为 文本内容方法TextNoHTML
不记得在哪看过这个,挺实用的 /// <summary> /// 将html文本转化为 文本内容方法TextNoHTML /// </summary> /// <para ...
