[乱搞]hdu 6406 Taotao picks apples 笛卡尔树+倍增

题目链接

Problem Description

There is an apple tree in front of Taotao's house. When autumn comes, n apples on the tree ripen, and Taotao will go to pick these apples.

When Taotao picks apples, Taotao scans these apples from the first one to the last one. If the current apple is the first apple, or it is strictly higher than the previously picked one, then Taotao will pick this apple; otherwise, he will not pick.

Given the heights of these apples h1,h2,⋯,hn, you are required to answer some independent queries. Each query is two integers p,q, which asks the number of apples Taotao would pick, if the height of the p-th apple were q (instead of hp). Can you answer all these queries?

Input

The first line of input is a single line of integer T (1≤T≤10), the number of test cases.

Each test case begins with a line of two integers n,m (1≤n,m≤105), denoting the number of apples and the number of queries. It is then followed by a single line of n integers h1,h2,⋯,hn (1≤hi≤109), denoting the heights of the apples. The next m lines give the queries. Each of these m lines contains two integers p (1≤p≤n) and q (1≤q≤109), as described in the problem statement.

Output

For each query, display the answer in a single line.

Sample Input

1
5 3
1 2 3 4 4
1 5
5 5
2 3

Sample Output

1
5
3

Hint

For the first query, the heights of the apples were 5, 2, 3, 4, 4, so Taotao would only pick the first apple.

For the second query, the heights of the apples were 1, 2, 3, 4, 5, so Taotao would pick all these five apples.

For the third query, the heights of the apples were 1, 3, 3, 4, 4, so Taotao would pick the first, the second and the fourth apples.

题意

有n个苹果，每个苹果有自己的高度，从第一个苹果开始，每次只能拿比上一次更高的苹果，直到遍历完所有苹果。有m次询问，每次假设第p个苹果的高度变成q，求在这样的情况下，能拿到几个苹果？

分析

这道题有很多做法，在线可以用线段树和二分，离线可以维护单调栈，都是代码量短，效率高的解法。本文章纯属自己瞎搞出来的解法，如果你是抱着想学习正解的心态不小心点进来了，为了避免误导，还是先去看大佬写的文章吧_(:з) ∠)_。
无论用哪一种算法，对于这道题目，最重要的就是高效的完成从一个苹果找到下一个苹果，那么笛卡尔树用来处理这样的操作是否足够呢？（笛卡尔树的解释可以参考这篇博客）
把一个数组按笛卡尔树的方式组织，根节点是整个数组最大的节点，然后以这个节点把数组划分为两部分，左右子结点分别又是左右部分的最大节点，以此类推。这样处理以后，从根节点一直向左走的路径，就是从第一个苹果出发将得到的递增序列。因此，我们只用考虑每次询问以后，这条路径会发生怎样的变化，而不必考虑整棵树的变化（如果树在不断更新就得考虑，只是需要进行非常细致的讨论）。询问大致可以分为4类：路径上的点变大/变小，非路径上的点变大/变小。

情况一：路径上的点变大
因为是增大，所以不会有新的点出现，只会覆盖已有的点。只需要从当前节点出发找到第一个比q大的节点就可以了。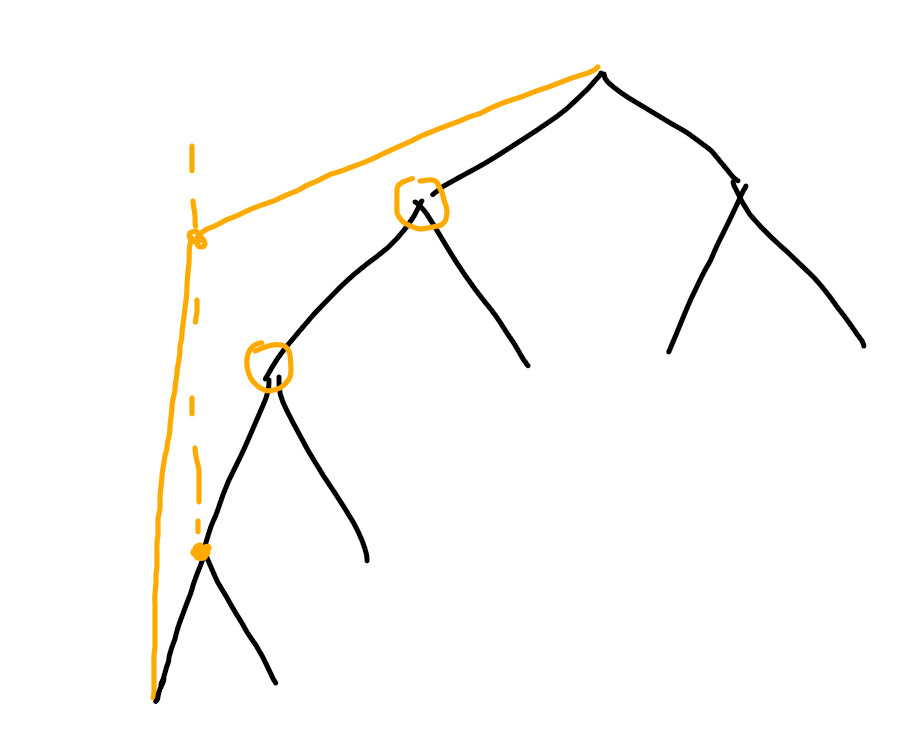

情况二：路径上的点变小
假设这个点是a，路径上的下一个点是b，那么当a变为a1的时候，在a，b之间本来被a覆盖的数字，就需要重新考虑。也就是从这个点右边的第一个数开始寻找，一直向上直到第一个比a1大的数。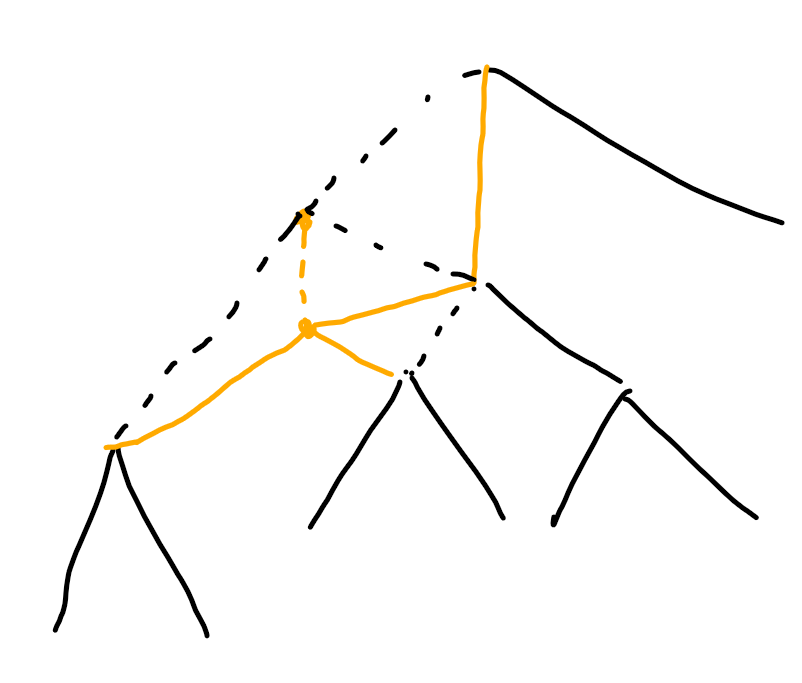

但是当a继续变小的时候，它将被路径上的前一个点c覆盖，而下一个点就应该是到第一个比c大的数

情况三：非路径上的点变大
考虑这个点在路径上的最近祖先。只有当它的变得比它的祖先还大，才会影响路径。而且它只会覆盖这个祖先的祖先。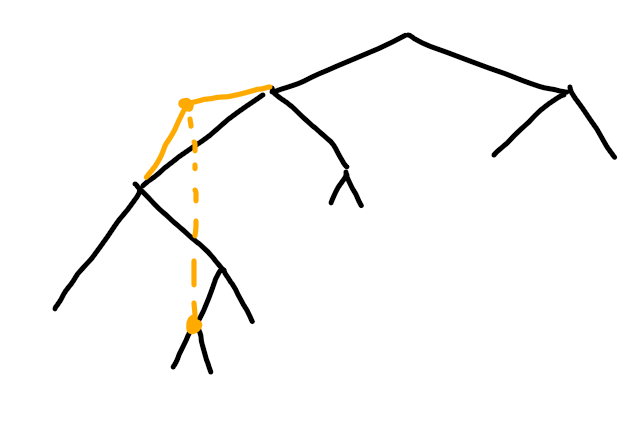

情况四：非路径上的点变小
对路径无影响
根据上面四个情况的分析，看似有很多边的变化，但最终只需要考虑有多少点要添加到路径上，其余的怎么变化不必考虑。
接下来就是终于到了算法的核心了，使用笛卡尔树只是将数组整理了成了一个比较好的结构，还需要一个高效寻找节点的方法。因为笛卡尔树的性质，向上走永远是在变大，每一个向上的过程都是单调的，可以用倍增的思想去寻找，每次尝试走1步，2步，4步，8步，直到遇到大的节点。
算法的复杂度不会算了，当时是这样分析的：建笛卡尔树为O(n)，每次查询找下一个节点的复杂度在O(log(n))以内，如果建出来的笛卡尔树比较平衡的话，甚至可能接近O(log(log(n)))，但因为数据随机以及可能有专门卡的数据，一次询问复杂度大致为O(log(n))，总共m次询问，最坏情况下也为O(mlogn)。

总结

从一开始想到笛卡尔树，就在瞎搞的路上越走越远，笛卡尔树的数据结构不复杂，如果要进行更新操作，比如插入，删除，其实节点的左右相对位置是没有变化的，该在左边的还是在左边，该在右边的还是在右边，在这题里相当于父亲和儿子在上下浮沉，夹在它们之间的子树也只是在不断更换父亲而已，而这些细节不必考虑，因为答案只要求个数，只需要关心最终路径有几个新增的点，或者有几个点被覆盖了。

代码

#include<stdio.h>
#include<memory.h>
#define  N_max 100005
int n, m, ipt[N_max];
//#define  debug  there_is_no_bug_at_all_and_you_should_not_be_able_to_see_these_words_:(

/*手动简易栈*/
int slen, stackhelp[N_max];
inline void push(int x) { stackhelp[slen++] = x; }
inline void pop() { slen--; }
inline int top() { return slen> ? stackhelp[slen - ] : -; }
inline void clear() { slen = ; }

//笛卡尔树
typedef struct {
    int l, r, p, v;
    void newnode() { l = -; r = -; p = -; v = ; }
}node;
node tree[N_max];
int g[N_max][];
int on[N_max]; int lay[N_max];
void treeinit() {
    clear();
    memset(g, , sizeof g);
    memset(lay, , sizeof lay);
    memset(on, , sizeof on);
    tree[].newnode();
    tree[].v = 0x3f3f3f3f;
    push();
}

void add(int id, int v) {
    tree[id].newnode();//准备好节点
    while (slen >  && tree[top()].v < v)pop();
    int rt = top();
    tree[id].v = v;
    if (tree[rt].r > ) {/*子树挂到id左边*/
        tree[tree[rt].r].p = id;
        tree[id].l = tree[rt].r;
    }
    //id挂到根右边
    tree[rt].r = id;
    tree[id].p = rt;
    push(id);//入栈
}

int fb;
void dfs1(int cur){/*求倍增数组，顺带标记一下节点的层数*/
    if (cur == -)return;
    lay[cur] = (cur==?:(lay[tree[cur].p] + ));
    g[cur][] = tree[cur].p;
    for (int i = ;; ++i) {
        fb = g[cur][i - ]; if (fb == )break;
        g[cur][i] = g[fb][i - ];
    }
    dfs1(tree[cur].l);
    dfs1(tree[cur].r);
}

int key;
int find(int cur) {//利用倍增的思想查找第一个比key大的节点
    if (cur == -)return -;
    if (tree[cur].v>key)return cur;

    int fb = g[cur][];
    if (tree[fb].v>key)return fb;
    int jmp = fb;
    for (int i = ;; ++i) {//向上试探
        fb = g[cur][i]; if (fb == )break;
        if (tree[fb].v>key)break;
        jmp = fb;
    }
    return find(jmp);//可能没有一次找到，继续向上试探
}

void color(int cur){//把一颗子树完全涂色为根节点
    if (cur == -)return;
    on[cur] = on[tree[cur].p];
    color(tree[cur].l);
    color(tree[cur].r);
}

void geton() {//从根节点出发，把路径标记出来，并把路径上节点的右子树涂色为该节点
    int cur = tree[].r;
    do { on[cur] = cur;color(tree[cur].r); cur = tree[cur].l; } while (cur != -);
}

int sol(int p,int q){
    int x,y;
    if(on[p]==p){//在路径上的操作
        if(tree[p].v<q){//变大，考虑将被覆盖的点的个数
            key = q; x = find(p);
            return lay[] - lay[p] +  + lay[x];
        }
        else{//变小
            if(tree[p].r==-){
                //没有右子树，则一定不会出现新的点，只考虑当前点是否会被前一个点覆盖
                return (lay[]- ((tree[p].l==-)?:(q <= tree[tree[p].l].v)));
            }
            //考虑将从右子树新增几个点到路径上
            key = q;
            if(tree[p].l!=-&&q<=tree[tree[p].l].v)
            //左边有点并且更新后比前一个点更小
                key = tree[tree[p].l].v;
            y = find(p + );
            return lay[] - (q <= tree[tree[p].l].v) + lay[y] - lay[p];
        }
    }
    else{//操作非路径上的点
        if (tree[p].v<q){//变大
            key = q; x = find(p);
            if(on[x]==x)//变大到足够影响原序列，考虑将被覆盖的点的个数
                return (lay[] - lay[on[p]] + lay[x]+(x!=on[p])+(q>tree[on[p]].v));
        }
        return (lay[]);//不足以影响，无变化
    }
    return ;//正常情况下不该出现的返回值（误
}

int main()
{
    int kase, p, q;
    scanf("%d", &kase);
    while (kase--)    {
        scanf("%d %d", &n, &m);
        treeinit();
        for (int i = ; i <= n; ++i){
            scanf("%d", ipt + i);
            add(i, ipt[i]);
        }
        lay[] = ;
        dfs1();
        geton();
        for (int i = ; i<m; ++i) {
            scanf("%d %d", &p, &q);
            printf("%d\n",sol(p,q));
        }
    }
    return ;
}