树的直径证明+HDU2196

首先把无向图变成一棵树，直径肯定由叶子组成。

有以下两种情况：

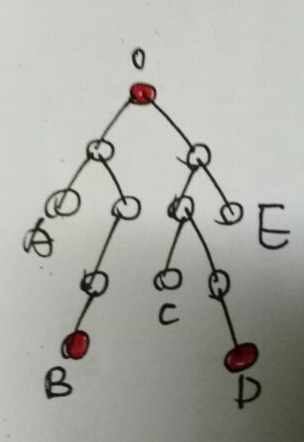
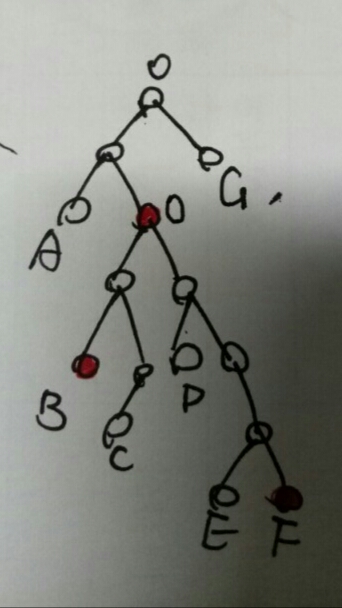
第一种：经过根节点，则找两个最远的叶子肯定是直径，也就是B+D。

第二种：不经过根节点，则目标的两个叶子肯定有一个不为根的公共祖先，如红点O，则在红点O下面找两个最远的叶子作为直径，找到了C+F。而很明显，这两个目标叶子中的其中一个（F）是距离根最远的叶子，因为如果两个叶子中不包含离根最远的点，则F经过根节点会找到更长的直径，矛盾。

则树的直径必然包括一个最远（深）叶子。先搜索到这个点（F），然后再搜索一次最远的点，可以得到树的直径。

这也说明，若把每个点（X）当成一个根，则直径的两个点（C+F）中的一个为X的最远点 ，所以找到直径C+F，则可以找到每个点在无向图中的最远距离：disCX or disFX

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<vector>
using namespace std;
int dis[],ans[];
int n,s,t;
vector<int>G[];
vector<int>L[];
void _dfs(int v)
{
    for(int i=;i<G[v].size();i++){
        if(!dis[G[v][i]]) {
            dis[G[v][i]]=dis[v]+L[v][i];
            _dfs(G[v][i]);
        }//任意两个点只有一条路，所以dfs和bfs效果一样
    }
}
void _finds()
{
      memset(dis,,sizeof(dis));
      dis[]=;_dfs();s=;
      for(int i=;i<=n;i++)
         if(dis[i]>dis[s]) s=i;

}
void _findt()
{
      memset(dis,,sizeof(dis));
      dis[s]=;_dfs(s);t=;
      for(int i=;i<=n;i++)
       if(dis[i]>dis[t]) t=i;
      for(int i=;i<=n;i++) ans[i]=dis[i]-;
}
void _tdis()
{
    memset(dis,,sizeof(dis));
    dis[t]=;
    _dfs(t);
    for(int i=;i<=n;i++)
     if(dis[i]->ans[i]) ans[i]=dis[i]-;
}
int main()
{
     int i,j,k,u,v;
     while(~scanf("%d",&n)){
            for(i=;i<=n;i++) {
               G[i].clear();
               L[i].clear();
            }
            for(i=;i<=n;i++){
                scanf("%d%d",&u,&v);
                G[u].push_back(i);
                L[u].push_back(v);
                G[i].push_back(u);
                L[i].push_back(v);
            }
            _finds();
            _findt();
            _tdis();
            for(i=;i<=n;i++)
            printf("%d\n",ans[i]);
     }
     return ;
}