Burnside引理和Polya定理
转载自:https://blog.csdn.net/whereisherofrom/article/details/79631703



Burnside引理和Polya定理的更多相关文章
- Burnside引理和Polya定理之间的联系
最近,研究了两天的Burnside引理和Polya定理之间的联系,百思不得其解,然后直到遇到下面的问题: 对颜色限制的染色 例:对正五边形的三个顶点着红色,对其余的两个顶点着蓝色,问有多少种非等价的着 ...
- Burnside引理和polay计数学习小记
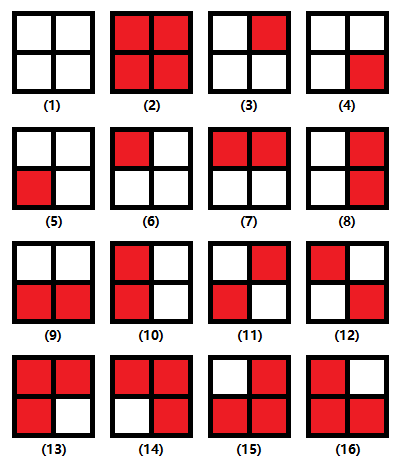
在组合数学中有这样一类问题,比如用红蓝两种颜色对2*2的格子染色,旋转后相同的算作一种.有多少种不同的染色方案?我们列举出,那么一共有16种.但是我们发现,3,4,5,6是同一种,7,8,9,10是用 ...
- 置换群和Burnside引理,Polya定理
定义简化版: 置换,就是一个1~n的排列,是一个1~n排列对1~n的映射 置换群,所有的置换的集合. 经常会遇到求本质不同的构造,如旋转不同构,翻转交换不同构等. 不动点:一个置换中,置换后和置换前没 ...
- Burnside引理与Polya定理
感觉这两个东西好鬼畜= = ,考场上出了肯定不会qwq.不过还是学一下吧用来装逼也是极好的 群的定义 与下文知识无关.. 给出一个集合$G = \{a, b, c, \dots \}$和集合上的二元运 ...
- Burnside引理与Polya定理 学习笔记
原文链接www.cnblogs.com/zhouzhendong/p/Burnside-Polya.html 问题模型 有一个长度为 $n$ 的序列,序列中的每一个元素有 $m$ 种取值. 如果两个序 ...
- Burnside引理和polay计数 poj2409 Let it Bead
题目描述 "Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you ...
- 【uva 10294】 Arif in Dhaka (First Love Part 2) (置换,burnside引理|polya定理)
题目来源:UVa 10294 Arif in Dhaka (First Love Part 2) 题意:n颗珠子t种颜色 求有多少种项链和手镯 项链不可以翻转 手镯可以翻转 [分析] 要开始学置换了. ...
- 等价类计数(Polya定理/Burnside引理)学习笔记
参考:刘汝佳<算法竞赛入门经典训练指南> 感觉是非常远古的东西了,几乎从来没有看到过需要用这个的题,还是学一发以防翻车. 置换:排列的一一映射.置换乘法相当于函数复合.满足结合律,不满足交 ...
- burnside引理&polya定理
burnside引理&polya定理 参考资料: <polya计数法的应用>--陈瑜希 黄学长 置换: 置换即是将n个元素的染色进行交换,产生一个新的染色方案. 群: 一个元素的集 ...
随机推荐
- Implicit super constructor xx() is undefined for default constructor. Must define an explicit constructor
错误:Implicit super constructor xx() is undefined for default constructor. Must define an explicit c ...
- [转]IIS的各种身份验证详细测试
本文转自:http://www.cnblogs.com/chnking/archive/2007/11/20/965553.html#_Toc183326163 一. IIS的身份验证概述 1. ...
- 小菜读书---《Effective C#:改善C#程序的50种方法》
一.用属性代替可访问的字段 1..NET数据绑定只支持数据绑定,使用属性可以获得数据绑定的好处: 2.在属性的get和set访问器重可使用lock添加多线程的支持. 二.readonly(运行时常量) ...
- C#三大特性之 封装、继承、多态
一.封装: 封装是实现面向对象程序设计的第一步,封装就是将数据或函数等集合在一个个的单元中(我们称之为类).被封装的对象通常被称为抽象数据类型. 封装的意义: 封装的意义在于保护或者防止代码(数据) ...
- [LeetCode]Generate Parentheses题解
Generate Parentheses: Given n pairs of parentheses, write a function to generate all combinations of ...
- CentOS6.5下连网以及输入法下载
宽带拨号连网: 1.系统--首选项--网络连接(或点击桌面右上角连网图标--VPN连接--VPN配置) 2.添加--选择DSL--勾自动连接(也可不勾)--DSL下填写用户名.密码--应用 ...
- 【数据库】java链接jdbc 释放资源
/* * 编写快速 入门的jdbc 程序 : * * 1. 先导入 具体的驱动jar包 * 2. 编写一个类 , 写jdbc 的程序 * * 具体的编写 java类的 代码的 ...
- Reporting Service 2005 迁移 到 2008
1. 备份ReportServer 和ReportServerTempDB 的数据库. 2. 在Reporting Services Configuration Manager 中备份Encrypti ...
- MySQL查询高速缓冲
对mysql的优化不在行,搞过几次优化,但是都不是很理想,还是浪费资源太多.一直发现我的mysql的缓存命中率极差,情况良好的时候到达过60-70%,但是运行时间一长,只有10-20%.查了一些资料, ...
- How To Install Cacti On Ubuntu 14
How To Install Cacti On Ubuntu 14.04/14.10 by anismaj Cacti is an open source web based network moni ...
