如何用Python实现常见机器学习算法-4

四、SVM支持向量机

1、代价函数

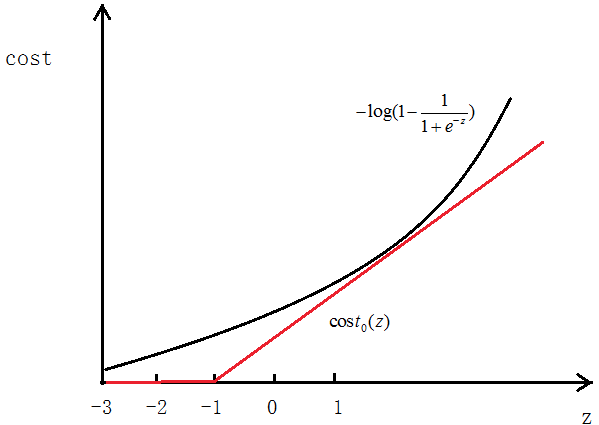
在逻辑回归中，我们的代价为：

其中：

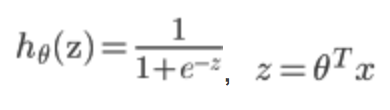
如图所示，如果y=1，cost代价函数如图所示

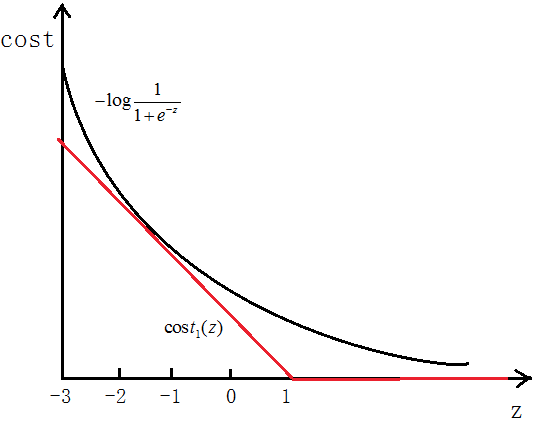
我们想让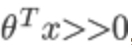，即z>>0，这样的话cost代价函数才会趋于最小（这正是我们想要的），所以用图中红色的函数代替逻辑回归中的cost

当y=0时同样用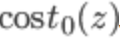代替

最终得到的代价函数为：

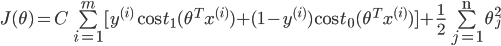
最后我们想要。

之前我们逻辑回归中的代价函数为：

可以认为这里的，只是表达形式问题，这里C的值越大，SVM的决策边界的margin也越大，下面会说明。

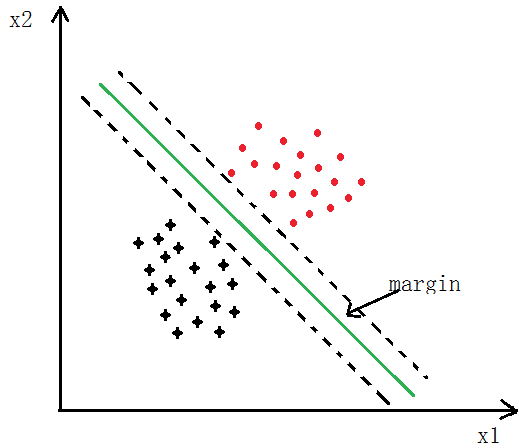
2、Large Margin

如下图所示，SVM分类会使用最大的margin将其分开

先说一下向量内积

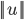表示U的欧几里德范数（欧式范数），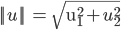

向量V在向量U上的投影的长度记为p，则：向量内积：

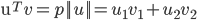
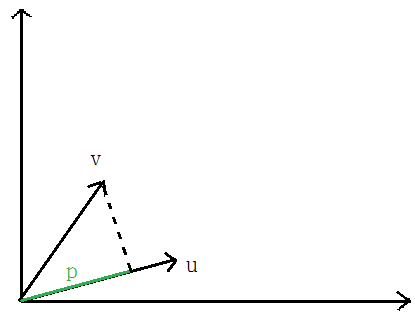
根据向量夹角公式推导一即可，

前面说过，当C越大时，margin也就越大，我们的目的是最小化代价函数J(θ)，当margin最大时，C的乘积项

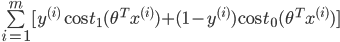
要很小，所以金丝猴为：

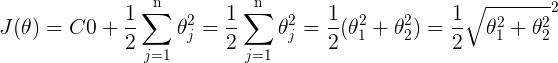
我们最后的目的就是求使代价最小的θ

由

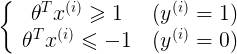
可以得到：

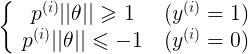
p即为x在θ上的投影

如下图所示，假设决策边界如图，找其中的一个点，到θ上的投影为p，则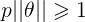或者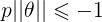，若是p很小，则需要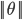很大，这与我们要求的θ使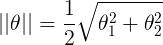最小相违背，所以最后求的是large margin

3、SVM Kernel（核函数）

对于线性可分的问题，使用线性核函数即可

对于线性不可分的问题，在逻辑回归中，我们是将feature映射为使用多项式的形式，SVM中也有多项式核函数，但是更常用的是高斯核函数，也称为RBF核

高斯核函数为：

假设如图几个点，

令：

，

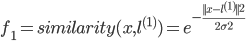可以看出，若是x与距离较近，可以推出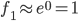，（即相似度较大）；

若是x与距离较远，可以推出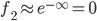，（即相似度较低）。

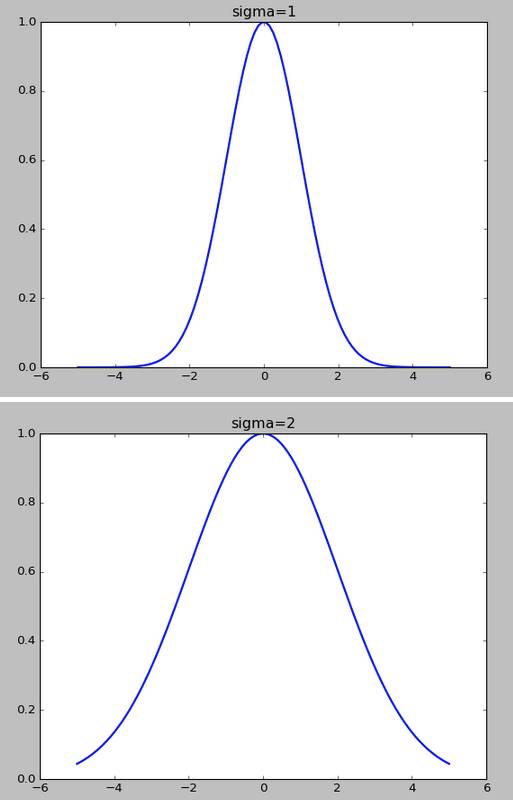
高斯核函数的σ越小，f下降的越快

如何选择初始的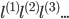

训练集：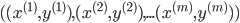

选择：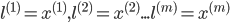

对于给出的x，计算f，令：，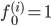

所以：

最小化J求出θ，

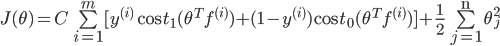
如果，==》预测y=1

4、使用scikit-learn中的SVM模型代码

全部代码

 import numpy as np
 from scipy import io as spio
 from matplotlib import pyplot as plt
 from sklearn import svm

 def SVM():
     '''data1——线性分类'''
     data1 = spio.loadmat('data1.mat')
     X = data1['X']
     y = data1['y']
     y = np.ravel(y)
     plot_data(X,y)

     model = svm.SVC(C=1.0,kernel='linear').fit(X,y) # 指定核函数为线性核函数
     plot_decisionBoundary(X, y, model)  # 画决策边界
     '''data2——非线性分类'''
     data2 = spio.loadmat('data2.mat')
     X = data2['X']
     y = data2['y']
     y = np.ravel(y)
     plt = plot_data(X,y)
     plt.show()

     model = svm.SVC(gamma=100).fit(X,y)     # gamma为核函数的系数，值越大拟合的越好
     plot_decisionBoundary(X, y, model,class_='notLinear')   # 画决策边界

 # 作图
 def plot_data(X,y):
     plt.figure(figsize=(10,8))
     pos = np.where(y==1)    # 找到y=1的位置
     neg = np.where(y==0)    # 找到y=0的位置
     p1, = plt.plot(np.ravel(X[pos,0]),np.ravel(X[pos,1]),'ro',markersize=8)
     p2, = plt.plot(np.ravel(X[neg,0]),np.ravel(X[neg,1]),'g^',markersize=8)
     plt.xlabel("X1")
     plt.ylabel("X2")
     plt.legend([p1,p2],["y==1","y==0"])
     return plt

 # 画决策边界
 def plot_decisionBoundary(X,y,model,class_='linear'):
     plt = plot_data(X, y)

     # 线性边界
     if class_=='linear':
         w = model.coef_
         b = model.intercept_
         xp = np.linspace(np.min(X[:,0]),np.max(X[:,0]),100)
         yp = -(w[0,0]*xp+b)/w[0,1]
         plt.plot(xp,yp,'b-',linewidth=2.0)
         plt.show()
     else:  # 非线性边界
         x_1 = np.transpose(np.linspace(np.min(X[:,0]),np.max(X[:,0]),100).reshape(1,-1))
         x_2 = np.transpose(np.linspace(np.min(X[:,1]),np.max(X[:,1]),100).reshape(1,-1))
         X1,X2 = np.meshgrid(x_1,x_2)
         vals = np.zeros(X1.shape)
         for i in range(X1.shape[1]):
             this_X = np.hstack((X1[:,i].reshape(-1,1),X2[:,i].reshape(-1,1)))
             vals[:,i] = model.predict(this_X)

         plt.contour(X1,X2,vals,[0,1],color='blue')
         plt.show()

 if __name__ == "__main__":
     SVM()

线性可分的代码，指定核函数为linear：

 '''data1——线性分类'''
     data1 = spio.loadmat('data1.mat')
     X = data1['X']
     y = data1['y']
     y = np.ravel(y)
     plot_data(X,y)

     model = svm.SVC(C=1.0,kernel='linear').fit(X,y) # 指定核函数为线性核函数
     plot_decisionBoundary(X, y, model)  # 画决策边界

非线性可分的代码，默认核函数为rbf

 '''data2——非线性分类'''
     data2 = spio.loadmat('data2.mat')
     X = data2['X']
     y = data2['y']
     y = np.ravel(y)
     plt = plot_data(X,y)
     plt.show()

     model = svm.SVC(gamma=100).fit(X,y)     # gamma为核函数的系数，值越大拟合的越好
     plot_decisionBoundary(X, y, model,class_='notLinear')   # 画决策边界

5、运行结果

线性可分的决策边界：

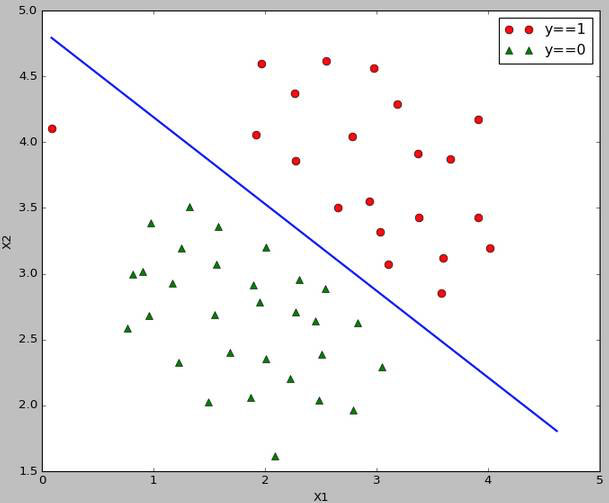
线性不可分的决策边界：

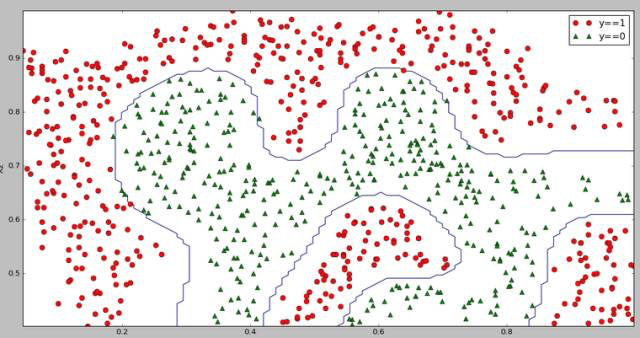
五、K-Means聚类算法

1、聚类过程

聚类属于无监督学习，不知道y的标记分为K类

K-Means算法分为两个步骤

第一步：簇分配，随机选K个点作为中心，计算到这K个点的距离，分为K个簇；

第二步：移动聚类中心，重新计算每个簇的中心，移动中心，重复以上步骤。

如下图所示

随机分配聚类中心：

重新计算聚类中心，移动一次

最后10步之后的聚类中心

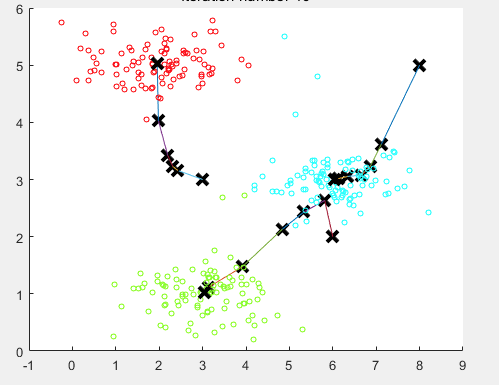
计算每条数据到哪个中心最近的代码如下：

 # 找到每条数据距离哪个类中心最近
 def findClosestCentroids(X,initial_centroids):
     m = X.shape[0]                  # 数据条数
     K = initial_centroids.shape[0]  # 类的总数
     dis = np.zeros((m,K))           # 存储计算每个点分别到K个类的距离
     idx = np.zeros((m,1))           # 要返回的每条数据属于哪个类

     '''计算每个点到每个类中心的距离'''
     for i in range(m):
         for j in range(K):
             dis[i,j] = np.dot((X[i,:]-initial_centroids[j,:]).reshape(1,-1),(X[i,:]-initial_centroids[j,:]).reshape(-1,1))

     '''返回dis每一行的最小值对应的列号，即为对应的类别
     - np.min(dis, axis=1)返回每一行的最小值
     - np.where(dis == np.min(dis, axis=1).reshape(-1,1)) 返回对应最小值的坐标
      - 注意：可能最小值对应的坐标有多个，where都会找出来，所以返回时返回前m个需要的即可（因为对于多个最小值，属于哪个类别都可以）
     '''
     dummy,idx = np.where(dis == np.min(dis, axis=1).reshape(-1,1))
     return idx[0:dis.shape[0]]  # 注意截取一下

计算类中心代码实现：

 # 计算类中心
 def computerCentroids(X,idx,K):
     n = X.shape[1]
     centroids = np.zeros((K,n))
     for i in range(K):
         centroids[i,:] = np.mean(X[np.ravel(idx==i),:], axis=0).reshape(1,-1)   # 索引要是一维的,axis=0为每一列，idx==i一次找出属于哪一类的，然后计算均值
     return centroids

2、目标函数

也叫做失真代价函数

最后我们想得到：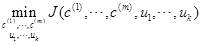

其中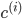表示i条数据距离哪个类中心最近，其中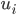即为聚类的中心

3、聚类中心的选择

随机初始化，从给定的数据中随机抽取K个作为聚类中心

随机一次的结果可能不好，可以随机多次，最后取使代价函数最小的作为中心。

代码实现：（这里随机一次）

 # 初始化类中心--随机取K个点作为聚类中心
 def kMeansInitCentroids(X,K):
     m = X.shape[0]
     m_arr = np.arange(0,m)      # 生成0-m-1
     centroids = np.zeros((K,X.shape[1]))
     np.random.shuffle(m_arr)    # 打乱m_arr顺序
     rand_indices = m_arr[:K]    # 取前K个
     centroids = X[rand_indices,:]
     return centroids

4、聚类个数K的选择

聚类是不知道y的label的，所以也不知道真正的聚类个数

肘部法则（Elbow method）

做代价函数J和K的图，若是出现一个拐点，如下图所示，K就取拐点处的值，下图显示K=3

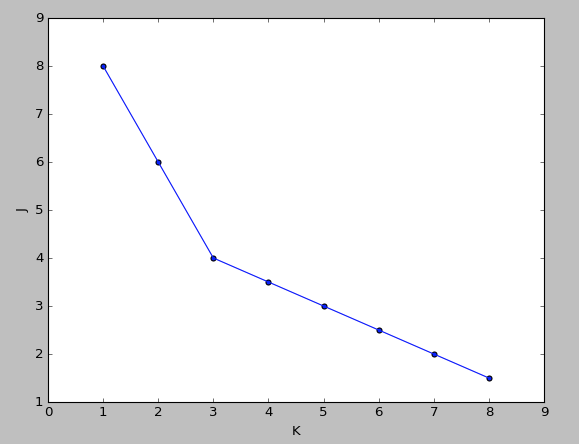
若是很平滑就不明确，人为选择。

第二种就是人为观察选择

5、应用-图片压缩

将图片的像素分为若干类，然后用这个类代替原来的像素值。

执行聚类的算法代码：

 # 聚类算法
 def runKMeans(X,initial_centroids,max_iters,plot_process):
     m,n = X.shape                   # 数据条数和维度
     K = initial_centroids.shape[0]  # 类数
     centroids = initial_centroids   # 记录当前类中心
     previous_centroids = centroids  # 记录上一次类中心
     idx = np.zeros((m,1))           # 每条数据属于哪个类

     for i in range(max_iters):      # 迭代次数
         print u'迭代计算次数：%d'%(i+1)
         idx = findClosestCentroids(X, centroids)
         if plot_process:    # 如果绘制图像
             plt = plotProcessKMeans(X,centroids,previous_centroids) # 画聚类中心的移动过程
             previous_centroids = centroids  # 重置
         centroids = computerCentroids(X, idx, K)    # 重新计算类中心
     if plot_process:    # 显示最终的绘制结果
         plt.show()
     return centroids,idx    # 返回聚类中心和数据属于哪个类

6、使用scikit-learn库中的线性模型实现聚类

 import numpy as np
 from scipy import io as spio
 from matplotlib import pyplot as plt
 from sklearn.cluster import KMeans

 def kMenas():
     data = spio.loadmat("data.mat")
     X = data['X']
     model = KMeans(n_clusters=3).fit(X) # n_clusters指定3类，拟合数据
     centroids = model.cluster_centers_  # 聚类中心

     plt.scatter(X[:,0], X[:,1])     # 原数据的散点图
     plt.plot(centroids[:,0],centroids[:,1],'r^',markersize=10)  # 聚类中心
     plt.show()

 if __name__ == "__main__":
     kMenas()

7、运行结果

二维数据中心的移动

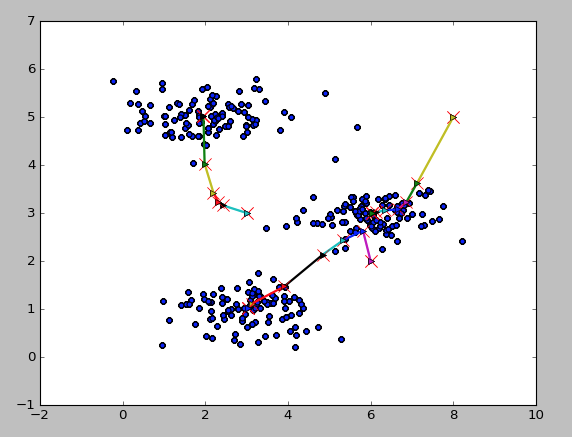
图片压缩