「算法笔记」树形 DP

一、树形 DP 基础

又是一篇鸽了好久的文章……以下面这道题为例，介绍一下树形 DP 的一般过程。

POJ 2342 Anniversary party

题目大意：有一家公司要举行一个聚会，一共有 $n$ 个员工，其中上下级的关系通过树形给出。每个人都不想与自己的直接上级同时参加聚会。每个员工都有一个欢乐度，举办聚会的你需要确定邀请的员工集合，使得它们的欢乐度之和最大，并且没有一个受邀的员工需要与他的直接上级共同参加聚会。$n\leq 6000$。

Solution：

考虑一个子树往上转移，发现除了子树的根选与不选的状态对上面的决策有影响之外，子树中其他的节点的状态都不用考虑。

设 ${dp}_{i,j}$ 表示以 $i$ 号节点为根的子树，$j$ 表示第 $i$ 号节点选或不选的状态（比如 $0$ 表示不选，$1$ 表示选）时，最大的子树中受邀的人的欢乐度之和。

${dp}_{u,0}=\sum\limits_{v\in son(u)} \max({dp}_{v,0},{dp}_{v,1})$（上级不参加舞会时，下级可以参加，也可以不参加）

${dp}_{u,1}=a_u+\sum\limits_{v\in son(u)} {dp}_{v,0}$（上级参加舞会时，下级都不会参加）

最后的答案就是 $\max({dp}_{root,0},{dp}_{root,1})$，时间复杂度 $O(n)$。

void dfs(int x,int fa){

    f[x][0]=0,f[x][1]=a[x];    //这里的 f 数组就是之前讲的 dp 数组

    for(int i=hd[x];i;i=nxt[i]){

        int y=to[i];

        if(y==fa) continue;

        dfs(y,x),f[x][0]+=max(f[y][0],f[y][1]),f[x][1]+=f[y][0];

    }

}

普通的树形 dp 中，常常会采用叶→根的转移形式，若子节点有多个，则需要一一枚举，将子节点（子树）的 dp 值合并。dp 的状态表示中，第一维通常是节点编号（代表以该节点为根的子树）。大多数时候，我们采用递归的方式实现树形 dp。

二、处理树上问题的基础

1. 树的重心

定义：树的重心也叫树的质心。对于一棵 $n$ 个节点的无根树，找到一个点，使得把树变成以该点为根的有根树时，最大子树的节点数最小。换句话说，删除这个点后最大连通块（一定是树）的节点数最小。

性质：

一棵树最多有两个重心，如果有两个重心，它们必定有一条边相连。
树中所有点到某个点的距离和中，到重心的距离和是最小的，如果有两个重心，它们的距离和一样。
把两棵树通过一条边相连，新的树的重心在原本两棵树重心的连线上。
一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。

求法：把树上的节点 $u$ 删除后，连通块为所有 $u$ 的每个儿子的子树以及 $u$ 的父亲连出去的整个连通块。如下图所示：

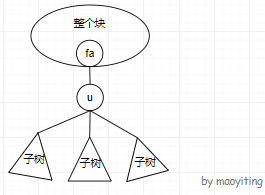
考虑 DFS 计算出每棵子树的节点个数。记 $sz_x$ 为以 $x$ 为根的子树大小。对于 $\forall v\in son(u)$，我们都可以通过 $sz_v$ 知道它的子树大小。那么 $u$ 的父亲连出去的整个连通块的大小就是 $n-sz_u$，其中 $n$ 为总节点数。所以我们可以直接计算删除每个点后的最大连通块的节点数。

于是我们可以枚举每个点，找到删除这个点后最大连通块的节点数最小的节点。

代码片段：

void dfs(int x,int fa){

    sz[x]=1,mx[x]=0;    //sz[x]:以 x 为根的子树大小。  mx[x]:删除点 x 后的最大连通块的节点数。

    for(int i=hd[x];i;i=nxt[i]){

        int y=to[i];

        if(y==fa) continue;

        dfs(y,x),sz[x]+=sz[y],mx[x]=max(mx[x],sz[y]);

    }

    mx[x]=max(mx[x],n-sz[x]);

    if(mx[x]<ans) ans=mx[x],id=x;    //找到删除这个点后最大连通块的节点数最小的节点。id:重心编号。注意 ans 初始化为无穷大。

}

2. 树的直径

定义：树中两点间的最长路径。（树的直径可能有很多条）

有一些不同的求法。

（1）通过 LCA 找出树的一条直径。

显然，一条直径上的所有点有一个共同的 $\text{LCA}$。在 DFS 的过程中对于每一个点，考虑以它为 $\text{LCA}$ 的可能的路径。

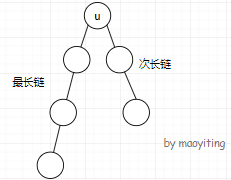
维护以每个点为顶端的最长链和次长链，然后用最长链加上次长链更新直径即可。

三、树形背包

Luogu P2014 选课

题目大意：共有 $n$ 门课，每门课有不同的学分。每门课没有或有唯一一门直接的先修课程。问在修 $m$ 门课的前提下，能够获得的最大学分数是多少？$n,m\leq 300$。

Solution：

因为每门课的先修课最多只有一门（对应着树中每个节点至多只有 $1$ 个父节点），所以这 $n$ 门课程构成了森林结构（若干棵树，因为可能有不止一门课没有先修课）。我们可以新建一门 $0$ 学分的课程（设这门课程编号为 $0$），作为“实际上没有先修课的课程”的先修课，把包含 $n$ 个节点的森林转化为包含 $n+1$ 个节点的树，其中节点 $0$ 为根节点。

令 ${dp}_{i,j}$ 表示在以 $i$ 为根的子树中选 $j$ 门课能够获得的最高学分。修完 $u$ 这门课后，对于所有的 $v_i\in son(u)$，我们可以在以 $v_i$ 为根的子树中选修若干门课（记为 $c_i$），在满足 $\sum c_i=t-1$ 的基础上获得尽量多的学分。

首先，显然有 ${dp}_{u,0}=0$。

${dp}_{u,t}=\max\limits_{\sum\limits_{i=1}^{\left| son(u)\right|}c_i=t-1}\begin{Bmatrix}\sum\limits_{i=1}^{\left| son(u)\right|} {dp}_{v_i,c_i}\end{Bmatrix}+a_x$

事实上，这是一个分组背包的模型。

总共有 $\left| son(u)\right|$ 组物品，每组物品都有 $t-1$ 个，其中第 $i$ 组的第 $j$ 个物品的体积为 $j$，价值为 ${dp}_{v_i,j}$，背包的总容积为 $t-1$。我们要从每组中选出不超过 $1$ 个物品（每个子结点 $v$ 只能选一个状态转移到 $u$），使得物品体积不超过 $t-1$ 的前提下（在修完 $u$ 后，还能选修 $t-1$ 门课），物品价值总和最大（获得最多学分）。特别地，$u=0$ 是一个特例，因为虚拟的根结点实际上不需要被选修，此时背包总体积应为 $t$。我们用分组背包进行树形 dp 的状态转移。

void dfs(int x,int fa){

    f[x][0]=0;

    for(int i=hd[x];i;i=nxt[i]){    //循环子节点（物品）

        int y=to[i];

        if(y==fa) continue;

        dfs(y,x);

        for(int t=m;t>=0;t--)    //倒序循环当前选课总门数（当前背包体积）

            for(int j=t;j>=0;j--)    //循环更深子树上的选课门数（组内物品）。此处使用倒序是为了正确处理组内体积为 0 的物品

                if(t-j>=0) f[x][t]=max(f[x][t],f[x][t-j]+f[y][j]);

    }

    if(x!=0) for(int t=m;t>0;t--) f[x][t]=f[x][t-1]+a[x];    //x 不为 0 时，选修 x 本身需要占用 1 门课，获得相应学分

}

这类题目被称为背包类树形 dp，它实际上是背包与树形 dp 的结合。除了以“节点编号”作为树形 dp 的阶段，通常我们也像线性 dp 一样，把当前背包的体积作为第二维状态。在状态转移时，我们要处理的实际上就是一个分组背包的问题。

四、换根 DP

给定一个树形结构，需要以 每个节点为根 进行一系列统计。

考虑朴素的解法：枚举每个节点，计算以它为根的答案。显然复杂度不够优秀。

我们一般通过两次扫描来求解此类题目：

1. 第一次扫描时，任选一个点为根，在“有根树”上执行一次 树形 DP，也就是在回溯时发生的、自底向上的状态转移。

2. 第二次扫描时，从刚才选出的根出发，对整棵树执行一次 深度优先遍历，在每次递归前进行自顶向下的推导，计算出“换根”后的解。

换言之，假设当前的根是当前节点的父亲，我们下一步需要将根换成当前节点。这样就可以一直做下去。具体来说，我们需要做两件事：

1. 把当前节点对父亲的贡献，从父亲的 dp 值里扣除（但不能直接修改，因为父亲还有别的儿子，所以最好做个备份）。

2. 把父亲（除去当前节点的贡献以后，剩余的部分）作为一个新的儿子，加入到当前节点的 dp 值中。这个是要直接修改的，因为要把当前节点换成根。

五、例题

1. HDU 6035 Colorful Tree

题目大意：给出一棵 $n$ 个节点的树，每个节点拥有一个颜色 $c_i$，现在定义两点间的距离为其路径上出现过的不同颜色数量。求两两点对距离之和。$n\leq 2000$。

Solution：

我们可以考虑每种颜色，统计经过该种颜色的路径条数。

补集转化，统计不经过该种颜色的路径条数。

可以想象成是将该种颜色的点在图中删去，剩下的每个连通块块内的路径数和就是答案。我们只要知道连通块的大小就可以求出相应的路径条数。

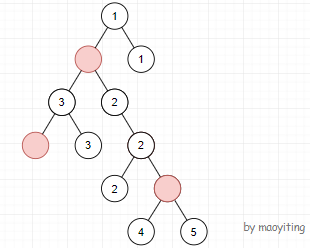
举个栗子，如图所示，树上所有的粉色节点将整棵树分为了 $5$ 个连通块（已在图中用数字标出）。

考虑颜色 $c$，它会把树分成很多个连通块，每个连通块会有 $C_{size}^2$ 的贡献。以 $1$ 号点为根，与根相连的连通块最后再特殊考虑，其他的连通块顶端会连着一个颜色为 $c$ 的点，在这个点处计算这个连通块的大小，设这个点为 $u$。

记 ${sum}_u$ 表示 $u$ 的子树中到 $u$ 的路径上不存在其他颜色为 $c$ 的点的个数。对 $u$ 的每个儿子 $v$，我们要算出 $v$ 的子树中所有颜色为 $c$ 的点的 $sum$ 的和 $S$，$sz_v-S$ 即为这个连通块的大小。利用 $S$ 我们也可以求出 ${sum}_u$。

#include<bits/stdc++.h>

#define int long long

#define MEM(x,y) memset(x,y,sizeof(x))

using namespace std;

const int N=2e5+5;

int t,n,m,x,y,c[N],tot,cnt,hd[N],to[N<<1],nxt[N<<1],sz[N],k[N],sum,v,ans;

bool vis[N];

void add(int x,int y){

    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;

}

void dfs(int x,int fa){

    sz[x]=1,k[c[x]]++;    //sz[x]:以 x 为根的子树大小

    int p=k[c[x]];    //原来与 c[x] 有关的节点数

    for(int i=hd[x];i;i=nxt[i]){

        int y=to[i];

        if(y==fa) continue;

        dfs(y,x),sz[x]+=sz[y],v=sz[y]-(k[c[x]]-p);    //v:当前子树中对应的连通量

        sum+=v*(v-1)/2,p=(k[c[x]]+=v);    //C(v,2)=v*(v-1)/2

    }

}

signed main(){

    while(~scanf("%lld",&n)){

        MEM(vis,0),MEM(hd,0),MEM(k,0),MEM(sz,0),cnt=tot=sum=ans=0;

        for(int i=1;i<=n;i++){

            scanf("%lld",&c[i]);

            if(!vis[c[i]]) tot++,vis[c[i]]=1;    //tot:颜色总数

        }

        for(int i=1;i<n;i++){

            scanf("%lld%lld",&x,&y);

            add(x,y),add(y,x);

        }

        dfs(1,0),ans=tot*n*(n-1)/2-sum;

        for(int i=1;i<=n;i++)

            if(vis[i]) v=n-k[i],ans-=v*(v-1)/2;

        printf("Case #%lld: %lld\n",++t,ans);

    }

    return 0;

}

2. CF1101D GCD Counting

题目大意：给出—棵 $n$ 个节点的树，每个节点上有点权 $a_i$。求最长的树上路径，满足条件：路径上经过节点（包括两个端点）点权的 $\gcd$ 不等于 $1$。$n\leq 2\times 10^5,1\leq a_i\leq 2\times 10^5$。

Solution：

$\gcd=d\neq 1$，那么肯定存在一个质数 $p$ 满足 $p\mid d$（即这条合法的链上的每个节点的点权都能被 $p$ 整除）。

令 ${dp}_{i,p}$ 表示以 $i$ 为根的子树中能被 $p$ 整除的最长链。

$2\times 3\times 5\times 7\times 11\times 13=30030>2\times 10^5$，所以 $dp$ 数组的第二维开 $6$ 就足够了。

只需要考虑以一个点为根的子树中，能够整除根的点权的质因子。

#include<bits/stdc++.h>

#define int long long

using namespace std;

const int N=2e5+5;

int n,a[N],x,y,cnt,hd[N],to[N<<1],nxt[N<<1],dp[N][6],ans;

vector<int>p[N];

void add(int x,int y){

    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;

}

void dfs(int x,int fa){

    for(int i=hd[x];i;i=nxt[i]){

        int y=to[i];

        if(y==fa) continue;

        dfs(y,x);

        for(int j=0;j<p[x].size();j++)    //枚举父亲的质因子

            for(int k=0;k<p[y].size();k++){    //枚举儿子的质因子

                if(p[x][j]!=p[y][k]) continue;    //如果两者不相等则跳过

                ans=max(ans,dp[x][j]+dp[y][k]);

                dp[x][j]=max(dp[x][j],dp[y][k]+1);     //转移

            }

    }

}

void solve(int x,int num){    //预处理每个点的质因子

    int cnt=0;

    for(int i=2;i<=sqrt(x);i++){

        if(x%i!=0) continue;

        p[num].push_back(i),dp[num][cnt++]=1;

        while(x%i==0) x/=i;

    }

    if(x!=1) p[num].push_back(x),dp[num][cnt++]=1;

}

signed main(){

    scanf("%lld",&n);

    for(int i=1;i<=n;i++){

        scanf("%lld",&a[i]),solve(a[i],i);

        if(a[i]!=1) ans=1;

    }

    for(int i=1;i<n;i++){

        scanf("%lld%lld",&x,&y);

        add(x,y),add(y,x);

    }

    dfs(1,0),printf("%lld\n",ans);

    return 0;

}

3. Luogu P3177「HAOI 2015」树上染色

题目大意：有一棵点数为 $n$ 的树，树边有边权。给你一个在 $0 \sim n$ 之内的正整数 $k$ ，你要在这棵树中选择 $k$ 个点，将其染成黑色，并将其他的 $n−k$ 个点染成白色。将所有点染色后，你会获得黑点两两之间的距离加上白点两两之间的距离的和的受益。问受益最大值是多少。$n,k\leq 2000$。

Solution：

考虑每条边对答案的贡献。即，边一侧的黑点数 $\times$ 另一侧的黑点数 $\times$ 边权 $+$ 一侧的白点数 $\times$ 另一侧的白点数 $\times$ 边权。

令 ${dp}_{u,t}$ 表示以 $u$ 为根的子树中，有 $t$ 个点被染成了黑色对答案贡献的最大值。

转化为了树形背包问题。

枚举更深子树上选择的黑点个数 $j$。${dp}_{u,t}=\max({dp}_{u,t},{dp}_{u,t-j}+{dp}_{v,j}+val)$。

边 $(u,v)$ 对答案的贡献 $val$：$val=j\times (k-j)\times w+(sz_v-j)\times (n-k-(sz_v-j))\times w$。

说明：$w$ 为 $(u,v)$ 的边权。$k$ 为总黑点数，$j$ 为边一侧的黑点数，那么边另一侧的黑点数就是 $k-j$。$sz_v$ 表示 $v$ 的子树大小，那么 $sz_v-j$ 就是边一侧的白点数。$n-k$ 为总白点数，则另一侧的白点数为 $n-k-(sz_v-j)$。

#include<bits/stdc++.h>

#define int long long

using namespace std;

const int N=2e3+5;

int n,k,x,y,z,cnt,hd[N],to[N<<1],nxt[N<<1],w[N<<1],sz[N],f[N][N];

void add(int x,int y,int z){

    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt,w[cnt]=z;

}

void dfs(int x,int fa){

    sz[x]=1,f[x][0]=f[x][1]=0;    //不选和只选一个一定合法，故把值赋为 0

    for(int i=hd[x];i;i=nxt[i]){

        int y=to[i];

        if(y==fa) continue;

        dfs(y,x),sz[x]+=sz[y];

        for(int t=min(k,sz[x]);t>=0;t--)    //枚举当前黑点数

            for(int j=0;j<=min(t,sz[y]);j++){    //枚举更深子树上的黑点数

                if(f[x][t-j]==-1) continue;    //不合法则跳过

                int val=j*(k-j)*w[i]+(sz[y]-j)*(n-k-(sz[y]-j))*w[i];    //val

                f[x][t]=max(f[x][t],f[x][t-j]+f[y][j]+val);    //转移

            }

    }

}

signed main(){

    memset(f,-1,sizeof(f));

    scanf("%lld%lld",&n,&k);

    for(int i=1;i<n;i++){

        scanf("%lld%lld%lld",&x,&y,&z);

        add(x,y,z),add(y,x,z);

    }

    dfs(1,0),printf("%lld\n",f[1][k]);

    return 0;

}

六、习题

HDU6201 transaction transaction transaction
HDU2196 Computer
UVA10859 放置街灯 Placing Lampposts
Luogu P4827 Crash 的文明世界（第二类斯特林数+换根 dp）