Causal Inference

目录

• Standardization
  • 非参数情况
  • Censoring
  • 参数模型
  • Time-varying
    • 静态
• IP weighting
  • 无参数
  • Censoring
  • 参数模型
    • censoring
    • 条件下 V
  • Time-varying
• G-estimation
  • 非参数模型
  • 参数模型
  • Time-varying
• Propensity Scores
• Instrumental Variables
  • Binary Linear Setting
  • Continuous Linear Setting
  • Nonparametric Identification
• Difference in Difference
• Doubly Robust Estimator
• Instrumental variable estimation
• Stratification
• Matching

Hern\(\'{a}\)n M. and Robins J. Causal Inference: What If.

Neal B. Introduction to Causal Inference.

graph LR
A(A) --> Y(Y)

graph LR
L(L) -->A(A) --> Y(Y)
L --> Y

这里对常用的causal effect的估计方法做一个总结, 需要注意的是, 在参数模型的情况下\(\theta L\) 表示\(\theta^TL\)当二者为向量的时候.

为了方便, 我们常常使用\(\sum\), 这并非要求该项必须是离散的, 除了\(A\)大部分可以等价于\(\int\).

默认情况下, (条件)可交换性(exchangeability), 一致性(consistency) 以及 正性(positivity) 都是满足的, 特别的情况为注明.

其中, time-varying的条件可交换性定义为:

\[(Y^g, \underline{L}_{k+1}^g) \amalg A_k | \bar{A}_{k-1} = g(\bar{A}_{k-2},\bar{L}_{k-1}), \bar{L}_{k}, \: k=0,\cdots, K.
\]

如果是静态的, \(g\)换成\(\bar{a}\).

Censoring 是数据缺失的情况, 对其的处理可以理解为对多个treatments的情况的处理.

Standardization

非参数情况

\[\mathbb{E}[Y^a] = \mathbb{E}[Y^a|A=a]= \mathbb{E}[Y|A=a].
\]

\[\tag{S}
\mathbb{E}[Y^a] = \mathbb{E}_{L} \mathbb{E}_{Y^a}[Y^a|L]
=\mathbb{E}_{L} \mathbb{E}_{Y}[Y|A=a, L].
\]

具体地, 为

\[\tag{S+}
\sum_l \mathbb{E}[Y|A=a, L=l] \mathrm{Pr}[L=l],
\]

所以该式必须满足正性, 即

\[\mathrm{Pr}[A=a|L=l] > 0, \quad \mathrm{if}\: \mathrm{Pr}[L=l] > 0,
\]

否则\(\mathbb{E}[Y|A=a, L=l]\)无定义.

Censoring

\[\mathbb{E}[Y^{a, c=0}] = \mathbb{E}_{L} \mathbb{E}[Y|A=a, C=0, L].
\]

参数模型

标准化处理的参数模型, 就是估计

\[\hat{\mathbb{E}} [Y|A=a, L=l],
\]

比如:

\[\hat{\mathbb{E}} [Y|A, L] = \theta_0 + \theta_1A + \theta_2L + \theta_3 AL.
\]

接下来用(S, S+)的公式就可以了(一般是直接用S, 根据大数定律弄的).

Time-varying

静态

\[\begin{array}{rl}
{}& \sum_{\bar{l}_K} \mathbb{E}[Y|\bar{A}_K=\bar{a}_K, \bar{L}_K=\bar{l}_K] \prod_{k=0}^K f(l_k|\bar{a}_{k-1}, \bar{l}_{k-1}) \\
=& \sum_{\bar{l}_K} \mathbb{E}[Y|\bar{A}_{K-1}=\bar{a}_{K-1}, \bar{L}_K=\bar{l}_K] \prod_{k=0}^K f(l_k|\bar{a}_{k-1}, \bar{l}_{k-1}) \\
=& \sum_{\bar{l}_K} \mathbb{E}[Y,\bar{A}_{K-1}=\bar{a}_{K-1}, \bar{L}_K=\bar{l}_K] \prod_{k=0}^{K-1} f(l_k|\bar{a}_{k-1}, \bar{l}_{k-1}) \cdot f(\bar{a}_{k-1}, \bar{l}_{k-1}) \\
=& \sum_{\bar{l}_K} \mathbb{E}[Y|\bar{A}_{K-1}=\bar{a}_{K-1}, \bar{L}_K=\bar{l}_{K-1}] \prod_{k=0}^{K-1} f(l_k|\bar{a}_{k-1}, \bar{l}_{k-1})\\
=& \cdots \\
=& \mathbb{E}[Y^{\bar{a}}].
\end{array}
\]

至于动态的, 书上给出了一个公式, 但是我感觉不是很对, 这里推导一下试试:

\[\begin{array}{rl}
{}& \mathbb{E}[Y^g] \\
=& \mathbb{E}_{\bar{a}\sim g} \mathbb{E}_Y [Y^{\bar{a}}] \\
=&\sum_{\bar{a}\sim g} \sum_{\bar{l}} \mathbb{E}[Y^{\bar{a}}|\bar{A}=\bar{a}, L=\bar{l}] \cdot f(\bar{A}, \bar{L}), \\
\end{array}
\]

其中

\[\mathrm{Pr}(\bar{A}, \bar{L}) = \prod_{k=0}^K f(L_k|\bar{A}_{k-1}, \bar{L}_{k-1}) \cdot \prod_{k=0}^K f^{int}(A_k|\bar{A}_{k-1}, \bar{L}_{k}).
\]

这里, \(f^{int}\)表示每一步\(g\)的根据前面历史选择\(A_k\)的概率.

IP weighting

无参数

\[\mathbb{E}[\frac{I(A=a)Y}{f(A|L)}] = \mathbb{E}_L \{\mathbb{E}_Y [Y^a|L] \cdot \underbrace{\mathbb{E}_{A}[\frac{I(A=a)}{f(A|L)}|L]}_{=1}\} = \mathbb{E}[Y^a].
\]

倘若\(A\)为连续变量, \(f\)为对应的条件密度函数, 则(非零的部分是零测集)

\[\mathbb{E}[\frac{I(A=a)Y}{f(A|L)}] \equiv 0.
\]

当正性不成立的时候, 即存在\(l\), \(\mathrm{Pr}[L=l] > 0\), 但是\(f(A=0|L=l) = 0\), 此时

\[\begin{array}{rl}
\mathbb{E}[\frac{I(A=a)Y}{f(A|L)}]
&= \mathbb{E}_{L \in Q(a)} \{\mathbb{E}[Y^a|L=l]\cdot \mathbb{E}_{A}[\frac{I(A=a)}{f(A|L)}|L]\} \\
&= \mathbb{E}_{L \in Q(a)} \{\mathbb{E}[Y^a|L=l]\} \\
&= \mathbb{E}[Y^a|L\in Q(a)]\mathrm{Pr}[L\in Q(a)]. \\
\end{array}
\]

Censoring

\[\mathbb{E}[Y^{a, c=0}] = \mathbb{E}[\frac{I(A=a, C=0)Y^a}{f(A|L)f(C|A,L)}].
\]

参数模型

定义

\[W^A = f(A|L),
\]

需要说明的是

\[\tag{IP}
\mathbb{E}[Y^a] = \frac{\mathbb{E}[I(A=a)W^AY]}{\mathbb{E}[I(A=a)W^A]}.
\]

注: 实际上分母为1.

特别的, 可以定义

\[SW^A = f(A) / f(A|L),
\]

\[\tag{IP+}
\mathbb{E}[Y^a] = \frac{\mathbb{E}[I(A=a)SW^AY]}{\mathbb{E}[I(A=a)SW^A]}.
\]

注: 此时分母为\(f(A)\). 在估计中, (IP+)更为稳定.

显然, 在参数模型中, 我们常常需要建模:

\[\hat{f}(A|L),
\]

并得到

\[\widehat{W}^A \quad \mathrm{or} \quad \widehat{SW}^A.
\]

此时再进一步假设

\[\hat{\mathbb{E}} [Y^a],
\]

比如

\[\hat{\mathbb{E}} [Y^a] := \theta_0 + \theta_1 a.
\]

通过\(\widehat{W}\)或者\(\widehat{SW}\)得到\(\mathbb{E}[Y^a]\)的近似值:

\[\frac{\sum_i I(A=a)W_iY_i}{\sum_i I(A=a)W_i},
\quad \mathrm{or} \quad
\frac{\sum_i I(A=a)SW_iY_i}{\sum_i I(A=a)SW_i}.
\]

通过最小二乘法来估计参数\(\theta_0, \theta_1\).

注: 一般情况下(\(A\)低维的情况), \(f(A)\)可以通过无参数估计估计, 否则也需要建模估计.

IP weighting 有一种特别好的思路, 主要到, 经过weighting之后, 相当于我们重新选择了\(A\), 此时\(A\)和\(L\)无关, 在这个伪造的人群中, 我们有

\[\mathbb{E}_{ps}[Y|A=a] = \mathbb{E}[Y^a].
\]

注: 证明只需要用到\(A \amalg L\).

注: 在这种可建模的情况下, 正性并不重要, 而且似乎即使\(A\)是连续变量, 上述的估计方式也是奏效的, 但是说实话我无法理解.

censoring

如果由censoring的情况出现, 只需要考虑

\[W^{AC} = W^A \cdot W^C, \\
SW^{AC} = SW^A \cdot SW^C, \\
\]

其中

\[W^C = 1 / f(C|A, L), \\
SW^C = f(C|A) / f(C|A, L).
\]

条件下 V

如何用IP weighting 估计

\[\mathbb{E}[Y^a|V], V \subset L.
\]

只需考虑

\[W^A = 1 / f(A| V, L\setminus V), \\
SW^A = f(A|V) / f(A, V, L\setminus V).
\]

分别利用(IP, IP+)即可.

注: 此时二者分母均不为1, 故不可用最普通的IP weighting的公式.

Time-varying

此时

\[W^{\bar{A}} = \prod_{k=0}^K \frac{1}{f(A_k|\bar{A}_{k-1}, \bar{L}_k)}, \\
SW^{\bar{A}} = \prod_{k=0}^K \frac{f(A_k|\bar{A}_{k-1})}{f(A_k|\bar{A}_{k-1}, \bar{L}_k)}. \\
\]

剩下的就是利用类似(IP, IP+)的公式计算.

在这种情况下, 同样有条件下V, 但是, 特别的是, \(V\)必须是baseline variables, 即

\[V \subset L_0.
\]

注: 没看到其用于动态策略的是说明.

G-estimation

非参数模型

非参数模型可以看成是参数模型的一种特例.

参数模型

这个方法主要是用于估计

\[\mathbb{E}[Y^a|L]
-\mathbb{E}[Y^{a'}|L].
\]

假设

\[\hat{\mathbb{E}} [Y^a|L] = \beta_0 + \beta_1 a + \beta_2 L + \theta_3 aL,
\]

则

\[\mathbb{E}[Y^a|L]
-\mathbb{E}[Y^{a=0}|L] = \beta_1 a + \beta_3 aV.
\]

假设 rank preserving 成立, 则有

\[Y^a = Y^{a=0} + \psi_0 a + \psi_1 aV, \\
\Rightarrow Y^{a=0} = Y - \psi_0 a - \psi_1 a V,
\]

并定义\(H(\psi^{\dagger}):= Y^{a=0}\).

注意到, 条件可交换性

\[Y^a \amalg A |L
\]

意味着

\[\mathrm{Pr}[A=1|Y^{a=0}, L]
= \mathrm{Pr}[A=1|L].
\]

假设我们用一个逻辑斯蒂回归对其进行建模:

\[\mathrm{logit}\:
\mathrm{Pr}[A=1|Y^{a=0}, L]
= \theta_0 + \theta_1 Y^{a=0} + \theta_2 Y^{a=0}V + \theta_3 L.
\]

则根据条件可交换性的性质, \(\theta_1, \theta_2\)都应该是0, 现在\(H(\psi^{\dagger})=Y^{a=0}\), 则

\[\mathrm{logit}\:
\mathrm{Pr}[A=1|H(\psi^{\dagger}), L]
= \theta_0 + \theta_1 H(\psi^{\dagger})+ \theta_2 H(\psi^{\dagger})V + \theta_3 L.
\]

给定\(\psi_0, \psi_1\), 我们可以估计出一组\(\theta_0, \cdots, \theta_3\), 什么样的\(\psi_0, \psi_1\)是好的, 就是让估计的参数\(\theta_1, \theta_2\)接近0.

所以 G-estimation 常用网格法来估计.

不过应对高维问题的时候就比较捉襟见肘了.

在特殊的情况下, 我们可以有显示的表达式.

Time-varying

类似.

\[\hat{\mathbb{E}}[Y^{\bar{a}_{k-1}, a_k, \underline{0}_{k+1}} - Y^{\bar{a}_{k+1}, \underline{0}_{k}}|\bar{A}_{k-1}=\bar{a}_{k-1}, \bar{L}_k = \bar{l}_k] = a_k \gamma_k (\bar{a}_{k-1}\bar{l}_k; \beta).
\]

\[Y^{\bar{A}_{k-1}, A_k, \underline{0}_{k+1}}
=Y^{\bar{A}_{k+1}, \underline{0}_{k}} + A_k \gamma_k (\bar{A}_{k-1}, \bar{l}_k ;\beta).
\]

\[H_k(\psi^{\dagger}) = Y - \sum_{j=k}^K A_j \gamma_j(\bar{A}_{j-1}, \bar{L}_{j}, \psi^{\dagger}).
\]

通过下式来估计:

\[\mathrm{logit}\:\mathrm{Pr} [A_k=1|H_k(\psi^{\dagger}), \bar{L}_k, \bar{A}_{k-1}] = \alpha_0 + \alpha_1 H_k(\psi^{\dagger}) + \alpha_2 W_k.
\]

Propensity Scores

该方法仅能应用于二元情形, 即\(A \in \{0, 1\}\).

当\(L\)是一个高维向量的时候, 一般的无参数模型就派不上用场了, 尽管我们可以通过参数模型来建模, 但是带来的结果是估计结果的方差会比较大.

我们记\(\pi(L) = \mathrm{Pr}[A|L]\), 并证明:

\[Y^a \amalg A | L \Rightarrow Y^a \amalg A | \pi(L).
\]

不妨假设\(\pi(L) =s \Leftrightarrow L \in \{l_i\}\), 则

\[\begin{array}{ll}
\mathrm{Pr}[Y^a|\pi(L)=s]
&= \mathrm{Pr} [Y^a|L \in \{l_i\}] \\
&= \frac{\sum_i\mathrm{Pr}[Y^a,L=l_i]}{\sum_i \mathrm{Pr} [L=l_i]}\\
&= \frac{\sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[L=l_i]}{\sum_i \mathrm{Pr} [L=l_i]}\\
&= \frac{\mathrm{Pr}[A=a|L=l] \cdot \sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[L=l_i]}{\mathrm{Pr}[A=a|L=l]\sum_i \mathrm{Pr} [L=l_i]}\\
&= \frac{\sum_i\mathrm{Pr}[Y|A=a, L=l_i]\mathrm{Pr}[A=a, L=l_i]}{\sum_i \mathrm{Pr} [A=a, L=l_i]}\\
&= \frac{\sum_i\mathrm{Pr}[Y, A=a, L=l_i]}{\sum_i \mathrm{Pr} [A=a, L=l_i]}\\
&= \frac{\mathrm{Pr}[Y, A=a, \pi(L)=s]}{\mathrm{Pr} [A=a, \pi(L)]}\\
&= \mathrm{Pr} [Y|A=a, \pi(L)=s].
\end{array}
\]

注意: \(\pi(l_i) = \pi(l_j) = \pi(l) = s\).

可见, 上述推导仅在\(A\)为二元变量是成立, 否则

\[\mathrm{Pr}[A=1|l] = \mathrm{Pr}[A=1|l'] \not \Rightarrow
\mathrm{Pr}[A=a'|l] = \mathrm{Pr}[A=a'|l'].
\]

也就无法保证上面的推导证明对于所有的\(A=a\)成立.

此时, 我们可以扩展causal graph为:

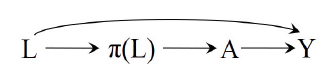
故, 我们可以通过\(\pi(L)\)来block以保证条件可交换性.

剩下的工作就是利用前面的方法了.

Instrumental Variables

graph LR
Z(Z)-->T(T) -->Y(Y)
U(U)-->T(T)
U(U)-->Y(Y)

instrumental variables 满足:

1. Z 对 T 有 causal effect;
2. Z 到 Y 的 causal effect 均通过 T, 即 T 是 Z 到 Y 所有 direct path 上的mediator;
3. Z 和 Y 之间不存在backdoor path.

Binary Linear Setting

CAG图如上图所示.

\[Y := \delta T + \alpha U.
\]

\[\begin{array}{rl}
\mathbb{E}[Y|Z=1] - \mathbb{E}[Y|Z=0]
=&\mathbb{E}[\delta T + \alpha U|Z=1] - \mathbb{E}[\delta T +\alpha U|Z=0] \\
=&\delta \mathbb{E}[[T|Z=1]-[T|Z=0]] + \alpha \mathbb{E}[[U|Z=1]-[ U|Z=0]] \\
=&\delta \mathbb{E}[[T|Z=1]-[T|Z=0]]
\end{array}
\]

故

\[\delta = \frac{\mathbb{E}[Y|Z=1] - \mathbb{E}[Y|Z=0]}{\mathbb{E}[T|Z=1] - \mathbb{E}[T|Z=0]}.
\]

注: 在此CAG图中, \(U \amalg Z\).

Continuous Linear Setting

依旧是如上的CAG图.

\[\begin{array}{rl}
\mathrm{Cov}(Y, Z) =
& \mathbb{E}[YZ] - \mathbb{E}[Y]\mathbb{E}[Z] \\
=& \delta (\mathbb{E}[TZ] - \mathbb{E}[T]\mathbb{E}[Z]) + \alpha
(\mathbb{E}[UZ] - \mathbb{E}[U]\mathbb{E}[Z]) \\
=& \delta \mathrm{Cov}(T, Z) + \alpha \mathrm{Cov}(U,Z)\\
=& \delta \mathrm{Cov}(T, Z)
\end{array}
\]

故

\[\delta = \frac{\mathrm{Cov}(Y, Z)}{\mathrm{Cov}(T, Z)}.
\]

注: 依然用到了\(U \amalg Z\).

Nonparametric Identification

仅考虑单个的二元变量\(T \in \{0, 1\}\), 有如下几种情况:

1. Compliers: \(T^{z=1}=1, T^{z=0}=0\).
2. Always-takers: \(T^{z=1}=1, T^{z=0}=1\).
3. Never-takers: \(T^{z=1}=0, T^{z=0}=0\).
4. Defiers: \(T^{z=1}=0, T^{z=0}=1\).

当我们所考虑的群体中仅包括前三种类型的时候, 显然有:

\[T_i^{z=1} \ge T_i^{z=0}.
\]

这是我们需要的单调性假设.

此时:

\[\mathbb{E}[Y^{t=1} - Y^{t=0}|T^{z=1}=1, T^{z=0}=0] =
\frac{\mathbb{E}[Y|Z=1]-\mathbb{E}[Y|Z=0]}{\mathbb{E}[T|Z=1]-\mathbb{E}[T|Z=0]}.
\]

即, 在compliers (遵照医嘱的) 的人群中, 可以计算出其causal effect.

证明在[2]的p93.

Difference in Difference

difference in difference 同样是处理存在unobservable变量时的一种有效的处理方法.

我们可以把\(Y^a\)拆成俩个阶段:

1. \(t=0\), 此时决定\(A\), 但是并没有落实\(A\);
2. \(t=1\), 实行\(A\).

凭借下面的假设:

1.

\[\forall t, \quad A=a \Rightarrow Y_t = Y_t^a.
\]

1. \(A=1\), \(A=0\)两个群体若都不施加治疗, 则结果一致:

\[\mathbb{E}[Y_1^0 - Y_0^0|A=1]
=\mathbb{E}[Y_1^0 - Y_0^0|A=0],
\]

1. 治疗前的状态一致:

\[\mathbb{E}[Y_0^1 - Y_0^0|A=1]=0.
\]

注: 上面的第二条假设可能不容易满足.

则:

\[\mathbb{E}[Y_1^1-Y_1^0|A=1]
=(\mathbb{E}[Y_1|A=1]-\mathbb{E}[Y_0|A=1])
-(\mathbb{E}[Y_1|A=0]-\mathbb{E}[Y_0|A=0]).
\]

Doubly Robust Estimator

未完待续

Instrumental variable estimation

未完待续

Stratification

未完待续

Matching

未完待续