McGan: Mean and Covariance Feature Matching GAN

目录

• 概
• 主要内容
  • Mean Matching IPM
    • prime
    • dual
  • Covariance Feature Matching IPM
    • prime
    • dual
  • 算法
• 代码

Mroueh Y, Sercu T, Goel V, et al. McGan: Mean and Covariance Feature Matching GAN[J]. arXiv: Learning, 2017.

@article{mroueh2017mcgan:,

title={McGan: Mean and Covariance Feature Matching GAN},

author={Mroueh, Youssef and Sercu, Tom and Goel, Vaibhava},

journal={arXiv: Learning},

year={2017}}

概

利用均值和协方差构建IPM, 获得相应的mean GAN 和 covariance gan.

主要内容

IPM:

\[d_{\mathscr{F}} (\mathbb{P}, \mathbb{Q}) = \sup_{f \in \mathscr{F}} |\mathbb{E}_{x \sim \mathbb{P}} f(x) - \mathbb{E}_{x \sim \mathbb{Q}} f(x)|.
\]

当\(\mathscr{F}\)是对称空间, 即\(f \in \mathscr{F} \rightarrow - f \in \mathscr{F}\),可得

\[d_{\mathscr{F}} (\mathbb{P}, \mathbb{Q}) = \sup_{f \in \mathscr{F}} \big \{\mathbb{E}_{x \sim \mathbb{P}} f(x) - \mathbb{E}_{x \sim \mathbb{Q}} f(x) \big\}.
\]

Mean Matching IPM

\[\mathscr{F}_{v,w,p}:= \{f(x)=\langle v, \Phi_w(x) \rangle | v\in \mathbb{R}^m, \|v\|_p \le 1, \Phi_w:\mathcal{X} \rightarrow \mathbb{R}^m, w \in \Omega\},
\]

其中\(\|\cdot \|_p\)表示\(\ell_p\)范数, \(\Phi_w\)往往用网络来表示, 我们可通过截断\(w\)来使得\(\mathscr{F}_{v,w,p}\)为有界线性函数空间(有界从而使得后面推导中\(\sup\)成为\(\max\)).

其中

\[\mu_w(\mathbb{P})= \mathbb{E}_{x \sim \mathbb{P}} [\Phi_w(x)] \in \mathbb{R}^m.
\]

最后一个等式的成立是因为:

\[\|x\|_* = \max \{\langle v, x \rangle | \|v\| \le 1\},
\]

又\(\| \cdot \|_p\)的对偶范数是\(\|\cdot\|_q, \frac{1}{p}+\frac{1}{q}=1\).

prime

整个GAN的训练过程即为

\[\tag{3}
\min_{g_\theta} \max_{w \in \Omega} \max_{v, \|v\|_p \le 1} \mathscr{L}_{\mu} (v,w,\theta),
\]

其中

\[\mathscr{L}_{\mu} (v,w,\theta) = \langle v, \mathbb{E}_{x \in \mathbb{P}_r} \Phi_w(x) - \mathbb{E}_{z \sim p(z)} \Phi_w(g_{\theta} (z)) \rangle.
\]

估计形式为

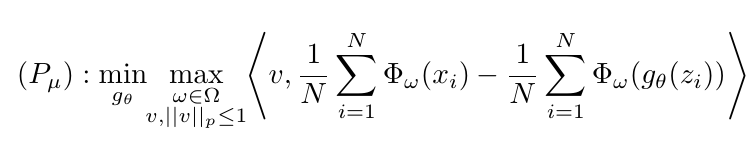
dual

也有对应的dual形态

\[\tag{4}
\min_{g_\theta} \max_{w \in \Omega} \|\mu_w(\mathbb{P}_r) - \mu_w (\mathbb{P}_{\theta})\|_q.
\]

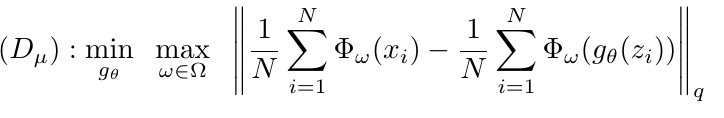
Covariance Feature Matching IPM

\[\mathscr{F}_{U, V,w} := \{f(x)= \sum_{j=1}^k \langle u_j, \Phi_w(x) \rangle \langle v_j, \Phi_w(x)\rangle, \langle u_i, u_j \rangle = \langle v_i, v_j \rangle =0, i \not = j, else \:1 \},
\]

等价于

\[\mathscr{F}_{U, V,w} := \{f(x)= \langle U^T \Phi_w(x), V^T\Phi_w(x) \rangle, U^TU=I_k, V^TV=I_k, w \in \Omega \}.
\]

并有

其中\([A]_k\)表示\(A\)的\(k\)阶近似, 如果\(A = \sum_i \sigma_iu_iv_i^T\), \(\sigma_1\ge \sigma_2,\ldots\), 则\([A]_k=\sum_{i=1}^k \sigma_i u_iv_i^T\). \(\mathcal{O}_{m,k} := \{M \in \mathbb{R}^{m \times k} | M^TM = I_k \}\), \(\|A\|_*=\sum_i \sigma_i\)表示算子范数.

prime

\[\tag{6}
\min_{g_\theta} \max_{w \in \Omega} \max_{U,V \in \mathcal{P}_{m, k}} \mathscr{L}_{\sigma} (U, V,w,\theta),
\]

其中

\[\mathscr{L}_{\sigma} (U,V,w,\theta) = \mathbb{E}_{x \sim \mathbb{P}_r} \langle U^T \Phi_w(x), V^T\Phi_w(x) \rangle- \mathbb{E}_{z \sim p_z} \langle U^T \Phi_w(g_{\theta}(z)), V^T\Phi_w(g_{\theta}(z)) \rangle.
\]

采用下式估计

dual

\[\tag{7}
\min_{g_{\theta}} \max_{w \in \Omega} \| [\Sigma_w(\mathbb{P}_r) - \Sigma_w(\mathbb{P}_{\theta})]_k\|_*.
\]

注: 既然\(\Sigma_w(\mathbb{P}_r) - \Sigma_w(\mathbb{P}_{\theta})\)是对称的, 为什么\(U \not =V\)? 因为虽然其对称, 但是并不(半)正定, 所以\(v_i=-u_i\)也是有可能的.

算法

代码

未经测试.

import torch
import torch.nn as nn
from torch.nn.functional import relu
from collections.abc import Callable
def preset(**kwargs):
    def decorator(func):
        def wrapper(*args, **nkwargs):
            nkwargs.update(kwargs)
            return func(*args, **nkwargs)
        wrapper.__doc__ = func.__doc__
        wrapper.__name__ = func.__name__
        return wrapper
    return decorator
class Meanmatch(nn.Module):
    def __init__(self, p, dim, dual=False, prj='l2'):
        super(Meanmatch, self).__init__()
        self.norm = p
        self.dual = dual
        if dual:
            self.dualnorm = self.norm
        else:
            self.init_weights(dim)
            self.projection = self.proj(prj)
    @property
    def dualnorm(self):
        return self.__dualnorm
    @dualnorm.setter
    def dualnorm(self, norm):
        if norm == 'inf':
            norm = float('inf')
        elif not isinstance(norm, float):
            raise ValueError("Invalid norm")
        p = 1 / (1 - 1 / norm)
        self.__dualnorm = preset(p=p, dim=1)(torch.norm)
    def init_weights(self, dim):
        self.weights = nn.Parameter(torch.rand((1, dim)),
                                    requires_grad=True)
    @staticmethod
    def _proj1(x):
        u = x.max()
        if u <= 1.:
            return x
        l = 0.
        c = (u + l) / 2
        while (u - l) > 1e-4:
            r = relu(x - c).sum()
            if r > 1.:
                l = c
            else:
                u = c
            c = (u + l) / 2
        return relu(x - c)
    @staticmethod
    def _proj2(x):
        return x / torch.norm(x)
    @staticmethod
    def _proj3(x):
        return x / torch.max(x)
    def proj(self, prj):
        if prj == "l1":
            return self._proj1
        elif prj == "l2":
            return self._proj2
        elif prj == "linf":
            return self._proj3
        else:
            assert isinstance(prj, Callable), "Invalid prj"
            return prj
    def forward(self, real, fake):
        temp = (real - fake).mean(dim=1)
        if self.dual:
            return self.dualnorm(temp)
        elif not self.training and self.dual:
            raise TypeError("just for training...")
        else:
            self.weights.data = self.projection(self.weights.data) #some diff here!!!!!!!!!!
            return self.weights @ temp
class Covmatch(nn.Module):
    def __init__(self, dim, k):
        super(Covmatch, self).__init__()
        self.init_weights(dim, k)
    def init_weights(self, dim, k):
        temp1 = torch.rand((dim, k))
        temp2 = torch.rand((dim, k))
        self.U = nn.Parameter(temp1, requires_grad=True)
        self.V = nn.Parameter(temp2, requires_grad=True)
    def qr(self, w):
        q, r = torch.qr(w)
        sign = r.diag().sign()
        return q * sign
    def update_weights(self):
        self.U.data = self.qr(self.U.data)
        self.V.data = self.qr(self.V.data)
    def forward(self, real, fake):
        self.update_weights()
        temp1 = real @ self.U
        temp2 = real @ self.V
        temp3 = fake @ self.U
        temp4 = fake @ self.V
        part1 = torch.trace(temp1 @ temp2.t()).mean()
        part2 = torch.trace(temp3 @ temp4.t()).mean()
        return part1 - part2