Adversarial Training with Rectified Rejection

概
主要内容
- rejection
- 实际使用
代码

Pang T., Zhang H., He D., Dong Y., Su H., Chen W., Zhu J., Liu T. Adversarial training with rectified rejection. arXiv Preprint, arXiv: 2105.14785, 2021.

概

通过对置信度进行矫正, 然后再根据threshold (1/2)判断是否拒绝. 有点detection的味道, 总体来说是很有趣的点子.

主要内容

假设一个网络$f_{\theta}$ 将样本$x$映射为概率向量$f_{\theta}(x)$, 则其置信度(confidence)为

\[f_{\theta}(x)[y^m], y^m := \mathop{\arg\max} \limits_{k} f_{\theta}(x)[k],
\]

若该样本的真实的标签为$y$, 进一步定义真实的置信度$\text{T-Con}$为

\[f_{\theta}(x)[y].
\]

我们进一步定义一个分类器$F$:

\[F(x) =
\left \{
\begin{array}{ll}
y^m & \text{if } f_{\theta}(x)[y] \ge \frac{1}{2}, \\
\text{don't know} & \text{if } f_{\theta}(x)[y] < \frac{1}{2}.
\end{array}
\right .
\]

显然这种情况下, 就算$f$训练得再糟糕, $F$都不会分错(虽然可能大部分都是拒绝判断, 但是拒绝判断在面对对抗样本的时候是有用的).

但是上面的情况是必须知道样本标签$y$的, 都知道标签了还弄个分类器不是多次一举. 所以我们现在要做的, 是做一个近似

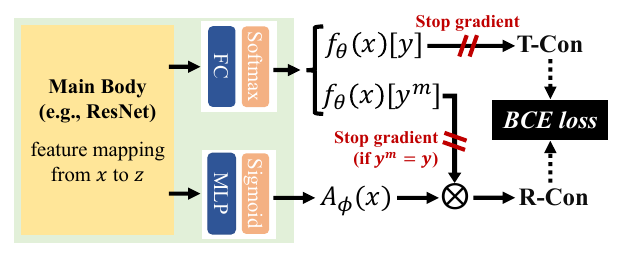
如上图所示, 我们要通过一个近似的$\text{R-Con}$来代替$\text{T-Con}$, Rectified Confidence通过如下的方式构建:

通过encoder将$x$映为特征$z$;
$z$通过全连接层和softmax层获得概率向量$f_{\theta}(x)$;
$z$通过MLP和sigmoid层获得$A_{\phi}(x) \in [0, 1]$;
计算Rectified Confidence:
\[\text{R-Con}(x) = f_{\theta}(x)[y^m]A_{\phi}(x).
\]

显然, 若要$\text{R-Con}(x) = \text{T-Con}(x)$, 则有

\[A_{\phi}(x) = A_{\phi}^*(x) = \frac{f_{\theta}(x)[y]}{f_{\theta}(x)[y^m]}.
\]

为此, 通过BCE损失:

\[\mathcal{L}_{RR}(x, y;\theta, \phi)
= \mathbf{BCE}(f_{\theta}(x)[y^m]A_{\phi}(x) \| f_{\theta}(x)[y]) \\
\mathbf{BCE}(f\|g) = g \cdot \log f + (1 - g) \cdot \log (1 - f).
\]

故总的损失为:

\[\min_{\theta, \phi}\: \mathbb{E}_{p(x y)}[\mathcal{L}_T(x^*, y;\theta) + \lambda \mathcal{L}_{RR}(x^*, y; \theta, \phi)], \\
x^* = \mathop{\arg \max} \limits_{x' \in B(x)} \mathcal{L}_{A}(x', y; \theta).
\]

注意图中的stop gradient部分, 最上面是为了一个单向的趋近(虽然encoder部分是会依然交涉), 第二个部分作者觉得当$y^m = y$时, 该样本比较简单, 而对抗学习应该注中难的样本, 这样不容易陷入局部最优, 经验之谈吧.

rejection

\[F(x) =
\left \{
\begin{array}{ll}
y^m & \text{if } \text{R-Con}(x) \ge \frac{1}{2}, \\
\text{don't know} & \text{if } \text{R-Con}(x) < \frac{1}{2}.
\end{array}
\right .
\]

现在的疑问是, 什么时候这个分类器是没有错判的.

定义: 当下列界,

$|\log (\frac{A_{\phi}(x)}{A_{\phi}^*(x)})| \le \log (\frac{2}{2-\xi})$;
$|A_{\phi}(x) - A_{\phi}^*(x)| \le \frac{\xi}{2}$

至少一个成立时, 称$A_{\phi}(x)$在点$x$处为$\xi\text{-error}$, $\xi \in [0, 1)$.

定理1: 假设$x_+, x_-$分别为被$f$正判和误判的样本, 即

\[y_+^m = y_+, y^m_- \not = y_-,
\]

但均满足(即置信度足够高)

\[f(x_+)[y_+^m] > \frac{1}{2-\xi}, \quad f(x_-)[y_-^m] > \frac{1}{2-\xi}, \: \xi \in [0, 1).
\]

若$A_{\phi}$在$x_+, x_-$处满足$\xi\text{-error}$, 则$\text{R-Con}(x_+) > \frac{1}{2} > \text{R-Con}(x_-)$, 即此时$F(x_+)$为正确判断, $F(x_-)$拒绝判断.

proof:

界1等价于:

\[\frac{2-\xi}{2}f(x)[y] \le \text{R-Con}(x) \le \frac{2}{2-\xi} f(x)[y],
\]

界2等价于

\[f(x)[y] - \frac{\xi}{2} f(x)[y^m] \le \text{R-Con}(x) \le f(x)[y] + \frac{\xi}{2} f(x)[y^m].
\]

因为

\[f(x_+)[y_+] = f(x_+)[y_+^m] > \frac{1}{2 - \xi},\\
\frac{2-\xi}{2}f(x_+)[y_+] > \frac{1}{2}, \\
f(x)[y] - \frac{\xi}{2} f(x)[y^m] = f(x)[y^m] - \frac{\xi}{2} f(x)[y^m] > \frac{1}{2}.
\]

所以$\text{R-Con}(x_+) > \frac{1}{2}$.

又因为

\[f(x)[y] \le 1 - f(x)[y^m] \Rightarrow f(x_-)[y_-] < \frac{1-\xi}{2-\xi}.
\]

易证

\[\frac{2}{2-\xi}\frac{1-\xi}{2-\xi} \le \frac{1}{2}, \xi \in [0, 1),
\]

\[f(x_-)[y_-] + \frac{\xi}{2}f(x_-)[y^m_-] \le 1 - t + \frac{\xi}{2}t < \frac{1}{2}, \quad t:= f(x_-)[y_-^m] > \frac{1}{2-\xi}.
\]

故$\text{R-Con}(x_-) < \frac{1}{2}$.

证毕.

实际使用

在实际使用中, threshold 似乎并不是固定为1/2, 而是通过TPR-FPR曲线选择的(TPR-95).

\[F(x) =
\left \{
\begin{array}{ll}
y^m & \text{if } \text{R-Con}(x) \ge t, \\
\text{don't know} & \text{if } \text{R-Con}(x) < t.
\end{array}
\right .
\]

代码

原文代码