2021.5.23 noip模拟2（排序|划艇|放棋子）

今天比昨天更惨，惨炸了

看到T1不会，跳！！！

T2不会，再跳！！！！

T3不会，后面没题了；；；；

无奈无奈，重新看T1，然鹅时间已经过去了一个小时

然而我一想不出题来就抱着水瓶子喝水，然后跑厕所，然后思路一直断。。。。

但是吧看到题解之后一切就恍然大悟了

哈哈哈哈没事慢慢锻炼，以后的考试一定得上100吧

看到这分数，怎么样，震惊到了吧，倒数第三那个是我，这都是大佬，别看我还有15分，蒙出来的，一点技术含量都没有

T1排序

N<=12;;;;

可以看到这数据属实很小啊

其实考场上我想到了正解，可惜我没敢打，（凭什么这题正解是dfs）那可是深搜啊！！！（暴力象征啊，怎么能是他呢？！？！？！？）

说正解吧；;

可以得到：对于所有操作来说，操作顺序对结果没有任何影响

（哼考场上我发现这个规律了，所以打了个阶乘就走了，没想到还有15pts）

所以我们可以从最小的i开始dfs

首先我们要判断这样的块中有多少不符合规律的（注意当前如果是2^x那么判断的时候要判断长度为2^x-1的区间（这很显然吧））

有四种情况：

　　1、有2个以上的不符合规律的区间。那就没法交换啦，只让交换一次，所以可以直接返回了，00000

　　2、没有不符合规律的。那就直接去下一层x+1

　　3、有1个不符合规律的区间。那就交换它前后的区间就行了

　　4、有2个不符合规律的区间。那么这时候可以两个不符合的互相交换，没准就成了呢（注意交换完了之后要判断，然后再换回去）判断成功后才能进入下一层

再定义一个计数器sum，记录一共交换了多少次

还有dfs的时候别忘了sum++，然后用完之后在sum--;

判断是否符合规律的时候有两种情况：1、前面的比后面的大

　　　　　　　　　　　　　　　　　2、前后的差值大于1（这个我是考后才发现的，原来这个区间里的数是连续的，一开始我还想离散化嘞！！！）

#include<bits/stdc++.h>
using namespace std;
#define re register int
const int N=1<<13;
int n,m,nn;
int a[N];
int jc[15],po[15];
int ans,sum;
bool flag(int l,int r){
    if(l==r)return true;
    for(re i=l+1;i<=r;i++)
        if(a[i]<a[i-1]||a[i]-a[i-1]>1)return false;
    return true;
}
void swp(int l,int r,int len){
    int b[N];
    for(re i=0;i<len;i++)b[i]=a[l+i];
    for(re i=0;i<len;i++)a[l+i]=a[r+i];
    for(re i=0;i<len;i++)a[r+i]=b[i];
}
void dfs(int x){
    int num=0;
    int p[100];
    for(re i=1;i<=po[n];i+=po[x])
        if(!flag(i,i+po[x]-1))
            p[++num]=i,p[++num]=i+po[x-1];
    if(num>4)return ;
    if(num==0)
        if(x==n)ans+=jc[sum];
        else dfs(x+1);
    else if(num==2){
        sum++;
        swp(p[1],p[2],po[x-1]);
        if(flag(p[1],p[1]+po[x]-1))
            if(x==n)ans+=jc[sum];
            else dfs(x+1);
        swp(p[1],p[2],po[x-1]);
        sum--;
    }
    else if(num==4){
        sum++;
        for(re i=1;i<=2;i++){
            for(re j=3;j<=4;j++){
                swp(p[i],p[j],po[x-1]);
                if(flag(p[1],p[1]+po[x]-1)&&flag(p[3],p[3]+po[x]-1))
                    if(x==n)ans+=jc[sum];
                    else dfs(x+1);
                swp(p[i],p[j],po[x-1]);
            }
        }
        sum--;
    }
}
int main(){
    scanf("%d",&n);
    po[0]=1;jc[0]=1;
    for(re i=1;i<=n;i++)jc[i]=jc[i-1]*i,po[i]=po[i-1]*2;
    for(re i=1;i<=po[n];i++){
        scanf("%d",&a[i]);
    }
    dfs(1);
    printf("%d",ans);
}

Code

T2划艇

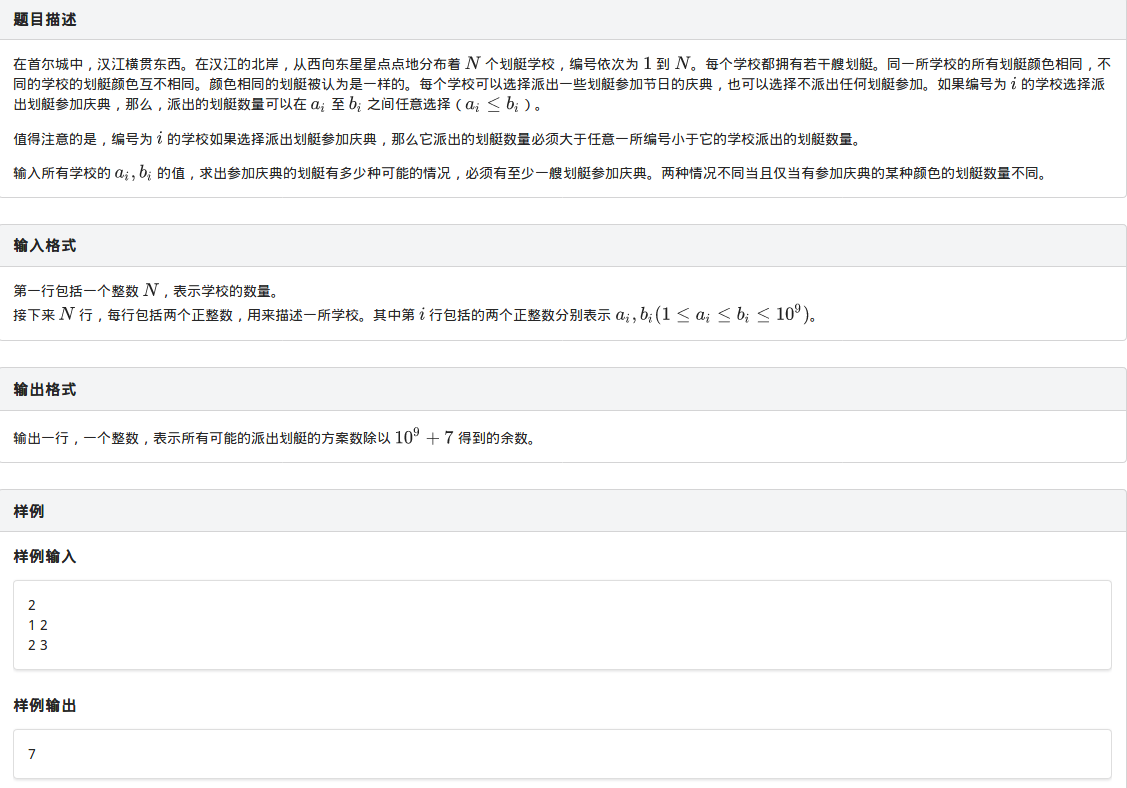
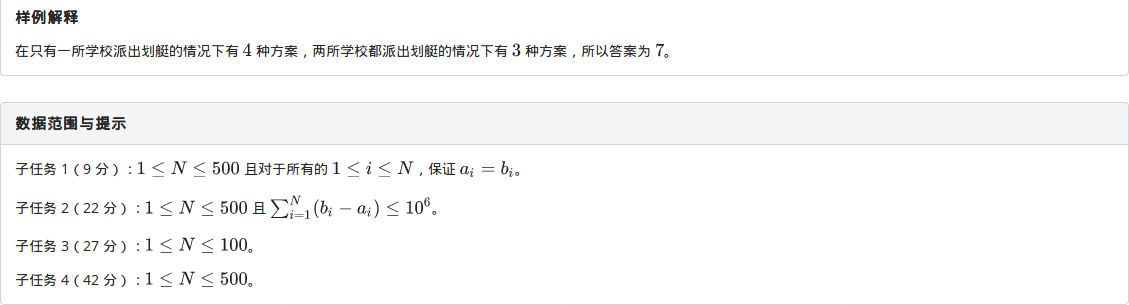
这是这场考试中最难的一个题了

考试的时候完全没有思路，想要通过dfs骗来9分没想到爆零了 ，害害害害害

首先想到的一定是dp;

（不对不对不对，首先想到的应该是离散化，毕竟数据范围太大了。。。QAQ）

设f[i][j]表示第i个学校派出j条船所能达到的方案数

啊呀，你突然就发现，这每个学校的a[i]和b[i]达到的区间会有重复的部分啊（完了完了完了转移不了了，然后你就放弃了dp，成功的躲避了正解）

凡事都得试试看啊，不试试就放弃，是不是傻啊

突然你就发现好像可以转移诶

这时候涉及到离散化的时候的一个小细节------------左闭右开（其实左开右闭也可以啦，都是为了让整个区间不重不漏，就看个人习惯了）

将a[i]和b[i]+1塞到离散化数组里，在设计转移方程的时候，注意循环的范围是(<)

转移的时候要分两种情况：

　　　　1、i-1这个学校派出的划艇不在a[i]~b[i]-1中，那么就可以直接转移，此时的i学校可以有方案数就是C(b[i]-a[i],1),那么再乘上前面所有的方案数就好了

　　（那么问题来了，怎么得到前面所有的方案数呢。。

　　　设sum[i][j]表示f[i][j]的二维前缀和，怎么求呢：sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+f[i][j];

　　　可能这也叫容斥原理吧，把多加上的给剪掉就好了）。

　　　　2、i-1和它以前的学校有一部分派出了在这个区间之内的划艇，那么就要再设一个未知数k，它表示从第k个开始，后面的学校派出了a[i]~b[i]-1只划艇

　　　　　这个转移比较难设计，f[i][j]+=组合数*sum[k-1][j-1];这个组合数怎么求呢

　　　（再引入一个数组，len[ ]，表示离散化数组里lsh[i]~lsh[i+1]的长度，（向后lsh[i+1]的长度，而不是向lsh[i-1]的，不然转移方程要修改的）

　　　　　首先我们要在了len[i]这么长的区间内寻找k个数（就像在一个递增区间内找k个数递增一样）有C(len[i],k)这么多种选择，当然这其中会有学校不派出划艇

　　　　　所以在i-k-1个学校中选出p-2学校来（不包括i和k）C(i-k+1,p-2)这个要乘好多p从1～i-k+1所以要手动搞一下，把它展开在合并，最后变成一个可以边转移边求出来的组合数，乘上就好了

还要注意，sum[i][j],不仅要吧a[i]~b[i]-1的f[i][j]加上，别的地方也要加上

然后我们就可以开开心心的把代码粘上了！！！！

记得开long long哟，不开long long见祖宗哦

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define re register int
const int mod=1e9+7;
const int N=505;
int n;
int l[N],r[N],len[N*2];
int lsh[N*2],lh,ls[N*2];
int inv[N];
int dp[N][N*2],sum[N][N*2];
map<int,int> p;
signed main(){
    scanf("%lld",&n);
    inv[1]=inv[0]=1;
    for(re i=2;i<=500;i++)
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    for(re i=1;i<=n;i++){
        scanf("%lld%lld",&l[i],&r[i]);
        lsh[i*2-1]=l[i];
        lsh[i*2]=r[i]+1;
    }
    sort(lsh+1,lsh+2*n+1);
    for(re i=1;i<=2*n;i++){
        if(lsh[i]!=lsh[i-1]){
            ls[++lh]=lsh[i];
            p[lsh[i]]=lh;
        }
    }
    for(re i=1;i<=n;i++){
        l[i]=p[l[i]];
        r[i]=p[r[i]+1];
    }
    sum[0][0]=dp[0][0]=1;
    ls[lh+1]=ls[lh]+1;
    for(re i=1;i<=lh;i++)len[i]=ls[i+1]-ls[i];
    for(re i=1;i<=n;i++)sum[i][0]=1;
    for(re i=1;i<=lh;i++)sum[0][i]=1;
    for(re i=1;i<=n;i++){
        for(re j=1;j<l[i];j++)
            sum[i][j]=(sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+dp[i][j]+mod)%mod;
        for(re j=l[i];j<r[i];j++){
            dp[i][j]=sum[i-1][j-1]*len[j]%mod;
            int c=len[j]-1;
            int can=1;
            for(re k=i-1;k>=1;k--){
                if(l[k]<=j&&j<r[k]){
                    can++;
                    c=c*((can+len[j]-2)*inv[can]%mod)%mod;
                    dp[i][j]=(dp[i][j]+sum[k-1][j-1]*c%mod)%mod;
                }
            }
            sum[i][j]=(sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+dp[i][j]+mod)%mod;
        }
        for(re j=r[i];j<=lh;j++)
            sum[i][j]=(sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+dp[i][j]+mod)%mod;
    }
    printf("%lld",sum[n][lh]-1);
}

Code

T3放棋子

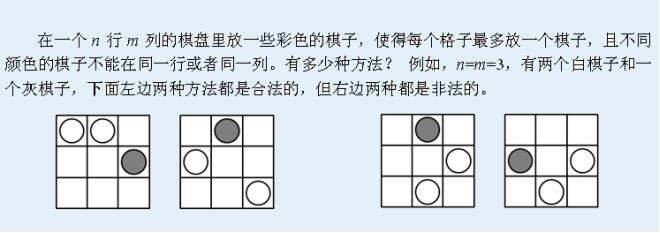
_{感谢赵队一句话点懂了我}

二维转移不了就用三维的啊

那么我瞬间感觉自己又行了

设f[i][j][k]为占据i行j列并且放了前k种颜色的棋子的方案数，然后你发现这根本不能直接求出来！！！

所以再设，g[i][j][k]为占据i行j列（这里指的是占满，就是前i行和前j列中哪个格子都不能再放其他种类的棋子了）并且放了k个相同种类的棋子

可以看到f[i][j][k]可以由f[1~i][1~j][ ]转移过来，那么这个式子我打不出来，所以你们自己看代码，总共五层循环！！！

　　f[i][j][k]转移的时候要乘组合数，就是空出哪几行和哪几列的方案数，最后要乘上g[i][j][col[k]]（col[k]就是输入的第k种棋子的个数）

那么g[i][j][k]咋求嘞，你又有重大发现，这个不能直接求 ------废话！！

还是容斥原理一下呗：g[i][j][k]=C(i*j,k)-g[a][b][k]*C(i,i-a)*C(j,j-b)就是减去那些有空行空列的情况

然后就是代码时间

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
const int mod=1e9+9;
int n,m,e;
int col[15];
ll f[35][35][15];
ll g[35][35][1005];
ll c[1005][1005];
ll ans;
signed main(){
    scanf("%d%d%d",&n,&m,&e);
    for(re i=1;i<=e;i++)
        scanf("%d",&col[i]);
    c[0][0]=1;
    for(re i=1;i<=1000;i++){
        c[i][0]=c[i][i]=1;
        for(re j=1;j<i;j++){
            c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
        }
    }
    for(re i=1;i<=n;i++)
        for(re j=1;j<=m;j++)
            for(re k=max(i,j);k<=i*j;k++){
                g[i][j][k]=c[i*j][k];
                for(re a=1;a<=i;a++)
                    for(re b=1;b<=j;b++){
                        if(a*b<k||(a==i&&b==j))continue;
                        g[i][j][k]=(g[i][j][k]-g[a][b][k]*c[i][a]%mod*c[j][b]%mod+mod)%mod;
                    }
            }
    f[0][0][0]=1;
    for(re i=1;i<=n;i++)
        for(re j=1;j<=m;j++){
            for(re k=1;k<=e;k++){
                if(i*j<col[k])continue;
                for(re a=0;a<=i;a++)
                    for(re b=0;b<=j;b++)
                        if((i-a)*(j-b)>=col[k])
                            f[i][j][k]=(f[i][j][k]+f[a][b][k-1]*c[n-a][i-a]%mod*c[m-b][j-b]%mod*g[i-a][j-b][col[k]]%mod)%mod;
            }
            ans=(ans+f[i][j][e])%mod;
        }
    printf("%lld",ans);
}

完结

∑l=1i−1∑r=1j−1f[l][r]+∑l=1k−1∑r=1j−1f[l][