图像数据到网格数据-1——Marching Cubes算法的一种实现
概述
之前的博文已经完整的介绍了三维图像数据和三角形网格数据。在实际应用中,利用遥感硬件或者各种探测仪器,可以获得表征现实世界中物体的三维图像。比如利用CT机扫描人体得到人体断层扫描图像,就是一个表征人体内部组织器官形状的一个三维图像。其中的感兴趣的组织器官通过体素的颜色和背景加以区别。如下图的人体足骨扫描图像。医生通过观察这样的图像可以分析病人足骨的特征,从而对症下药。
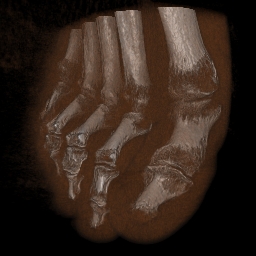
这类应用在计算机领域叫做科学可视化。由于本文主要不是讨论可视化这个大的命题,所以只是简要的讲述一下三维可视化的两大类实现方式,以及介绍一下用于面绘制方式的经典MarchingCubes算法,通过自己的理解来简单的实现这一算法,如果想详细的了解更多的内容,可以参考维基百科关于Scientific visualization的词条。
三维可视化的两种方式
简单点说,三维可视化的目的就是让人们从屏幕上看到三维图像中有什么东西。众所周知,二维图像的显示是容易的,但是三维图像却不一样。过去由于技术的限制,得到了三维图像的数据,只能把它以二维图像的切片的形式展示给人看,这样显然不够直观。随着计算机科学的发展,使用计算机图形学技术为三维物体建模并实时渲染,实现场景漫游变成显示三维物体的主流方法,而过去切片显示的方式则逐渐被边缘化。
由计算机图形学的知识我们可以知道,想显示三维图像中的内容,可以对这个“内容”的表面建立一个三角形网格模型。一旦得到了这个三角网格,那么渲染它就能够在屏幕上看到想要的内容,同时可以调节视角进行全方位的观察。所以第一类三维可视化方法就是基于这种思想:首先建立网格模型,之后渲染网格。这种方式被称为面绘制。下图就是对一个体数据中的虾建立表面模型之后的形态。

还有一种叫做体绘制的方式,是直接将三维图像的体素点通过一定的透明度叠加计算后直接对屏幕上的像素点着色。这种方式的特点是能更加清楚的表现体数据内部细节,但是这种算法一般对计算机的压力也会比较大。下图就是使用专门的体绘制软件来显示同一个数据中的虾的形态。
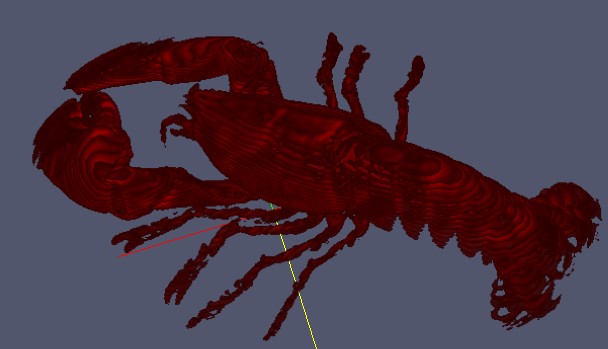
本文主要针对第一种算法,使用经典MarchingCubes算法(简称MC算法)的核心思想进行简要介绍,注意本文实现MC算法的方式与最初的WE Lorensen在1987年发表的论文里的实现的方式有所区别。本文会在后面谈及这一区别。
从图像到网格-MarchingCubes算法
从图像到网格的算法并非只有MC算法,但是MC算法相比其他的算法,具有生成网格的质量好,同时具有很高的可并行性的优点。所以在众多的行业应用中,MC算法以及各种类型的基于其思想的改进算法的使用频率是非常高的。
首先基于MC的一系列算法需要明确一个“体元(Cell)”的概念。体元是在三维图像中由相邻的八个体素点组成的正方体方格,MarchingCubes算法的Cube的语义也可以指这个体元。注意区别体元和体素,体元是8个体素构成的方格,而每个体素(除了边界上的之外)都为8个体元所共享。

一个宽高层数分别为width、height、depth的三维图像,其体素的对应的x,y,z方向的索引范围分别0~width-1、0~height-1、0~depth-1。容易想像出,这个体可以划分出(width-1)*(height-1)*(depth-1)个体元。为了给每个体元定位,对于一个特定的体元,使用这个体元x、y、z方向上坐标都是最小的那个体素(见上图)作为基准体素,以它的x、y、z索引作为这个体元的x、y、z索引。这样我们可以把这个Cube中的体素进行编号如下表所示:
| 体素位置 | 索引编号 | 体素代号 | 体素偏移(相对基准体素) | 位标记 |
| 上层,左侧,靠前 | 0 | VULF | (0,1,1) | 1<<0=1 |
| 上层,左侧,靠后 | 1 | VULB | (0,1,0) | 1<<1=2 |
| 下层,左侧,靠后 | 2 | VLLB | (0,0,0) | 1<<2=4 |
| 下层,左侧,靠前 | 3 | VLLF | (0,0,1) | 1<<3=8 |
| 上层,右侧,靠前 | 4 | VURF | (1,1,1) | 1<<4=16 |
| 上层,右侧,靠后 | 5 | VURB | (1,1,0) | 1<<5=32 |
| 下层,右侧,靠后 | 6 | VLRB | (1,0,0) | 1<<6=64 |
| 下层,右侧,靠前 | 7 | VLRF | (1,0,1) | 1<<7=128 |
示意图如下所示:

这样就可以为整个三维图像的体元和体素定位,同时为MC算法的实现做准备。同时根据下文的MC算法需要,用相同的思路为体元的边也进行编号定位:
| 图示 | 表说明 | ||||||||||||||||||||||||||
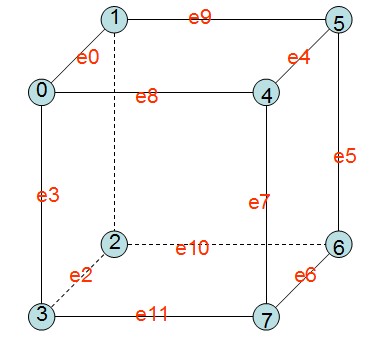 |
|
MC算法的主要思路是以体元为单位来寻找三维图像中内容部分与背景部分的边界,在体元抽取三角片来拟合这个边界。为了简单起见,我们将包含体数据内容的体素点称为实点,而其外的背景体素点都称作虚点。这样一个三维图像就是由各种实点和虚点组成的点阵。从单个体元的角度出发,体元的8个体素点每个都可能是实点或虚点,那么一个体元一共有2的8次方即256种可能的情况。MC算法的核心思想就是利用这256种可以枚举的情况来进行体元内的等值三角面片抽取。
一个体元的体素分布有256种,下文中使用“体素配置”和“体元配置”这两个词来指代这种分布情况。由于计算机内的位0,1字节位(bit)可以用来对应表示一个体素点是否是实点,这样可以正好使用一个字节中的8个位来分别对应一个体元中八个体素的分布情况。上文中的表已经把每个体素点所对应的字节位的位置表述清楚了,编号0~7的体素点的虚实情况分别对应一个字节中从右往左第1~8个位。比如一个字节二进制为01110111,则可以用来表示0,1,2,4,5,6号体素为实点,3,7,8号体素为虚点的体素配置。
总的来说,一个三维图像中任何一个体元都一定有一个字节对应着他的体素配置。这样,我们就可以顺序访问一个三维图像中的所有体元,为每个体元找出其配置。对于一般的三维图像来说,一个体元有很大概率8个体素全是虚的,或者全是实的,我们把这些体元叫做虚体元和实体元;而第三种情况是这个算法最为关心的,就是一个体元中既有实点也有虚点,这样的体元我们称其为边界体元。
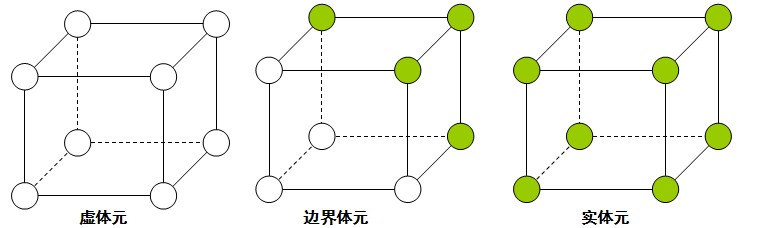
边界体元之所以重要,是因为其中必然包含了所谓的“等值面”。所谓等值面是指空间中的一个曲面,在该曲面上函数F(x, y, z)的值等于某一给定值Ft,即等值面是由所有点S = {(x, y, z):F(x, y, z) = Ft}组成的一个曲面。这个等值面能够表征图像虚实部分的边界。下图使用二维图片的等值线来说明:
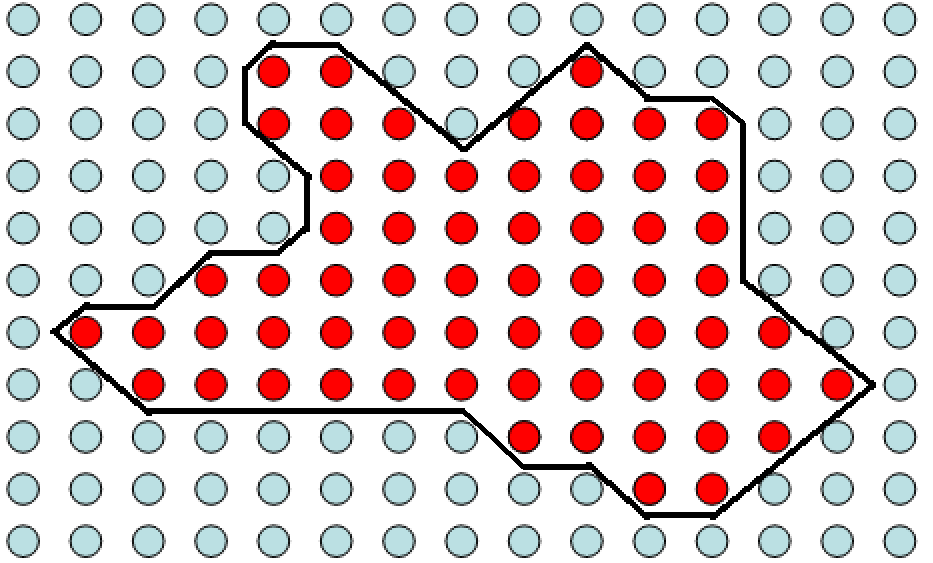
假设上图中红点表示像素值为250的像素,绿点表像素值为0的点。结合等高线的思想,可以将250的区域想象成一片海拔为250的高原,而0的区域是海拔为0的平原。则等值线为128的线就必然处在每个红点和绿点之间。相当于在一个由0过渡到250的坡上。实际上,值为1~249的等值线也都基本处在红点和绿点之间的位置。那么只要求出这些值中其中一个值的等值线,相当于就获得了250像素与0像素在几何意义上的边界。那么同样的道理,在三维图像中想求出介于实点和虚点之间的表面,就要在他们的边界,也就是边界体元内做文章,设法求出虚实体素之间的等值面。MC算法的另外一大思想就是使用三角片去拟合等值面。因为一个体元相对于图像是一个极小的局部,所以穿过该体元等值面就可以近似由小三角形片来拟合。例如下面的体元配置,我们就可以认为等值面的一部分就是以这样的方式穿过体元。
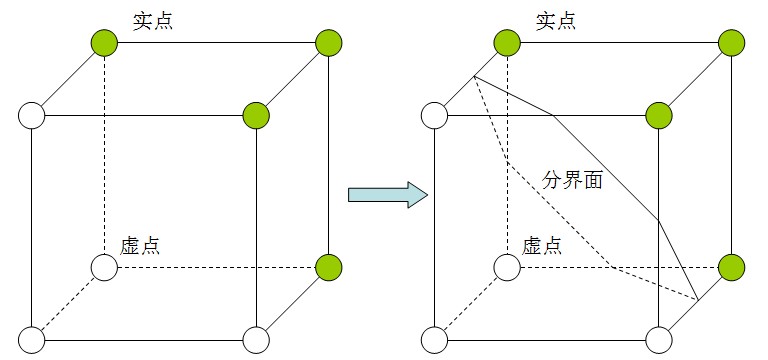
通过对256种体元(其中254种边界体元)配置的分析可以得知,256种体元配置中生成的等值三角片形式都能够被归纳为如下15种构型:

所有的256种配置都是这15种基本构型由旋转,对称变换等操作转变而成。每一种体元配置中等值面都是由若干个三角形片构成。这样针对这些有限的三角片分布情况,可以制作一个表来表示所有256种配置的三角形情况,这个表一共有256行,每行能表示该体元配置下三角形的情况。从图中可以看出,组成等值面的三角形的三个顶点一定是穿过体元的边的,所以可以用三条边的索引来表示一个三角形。如下图的体元配置:
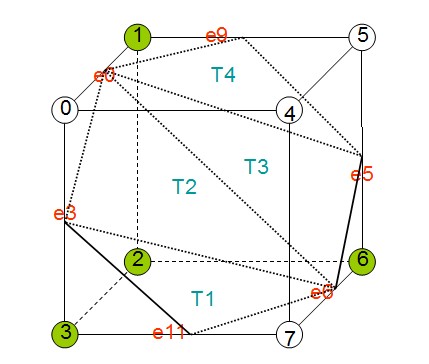
其实点为1,2,3,6,则其字节形式来表示8个体素的虚实情况为01001110,转为十进制为78。其等值面由4个三角形T1、T2、T3、T4组成这四个三角形的顶点分别所在边如下表所示:
| 三角形 | 顶点所在边 |
| T1 | e3,e11,e6 |
| T2 | e0,e3,e6 |
| T3 | e0,e6,e5 |
| T4 | e0,e5,e9 |
那么对于78这个体元配置,我们在表中就可有如下的记录(注意该表完整应该有256行而这里只写了78这一行):
| 体元配置 | 二进制形式 | 实点 | 三角形集合 |
| .... | .... | ... | ... |
| 78 | 01001110 | 1,2,3,6 | (3,11,6),(0,3,6),(0,6,5),(0,5,9) |
| .... | .... | ... | ... |
实际上,MC算法的三角形表就是将这样的方式简化后转化成二维数组来组织的,下面的代码就是MC的三角形表,具体是来源于网络流传,这张表应该不是计算机生成的,应该是在较早的时候有人手动统计的,他考察了所有256种情况的体元配置并画出其中的三角形,然后写在表里,这个活儿工作量不小,之后网上很多版本的MC算法都用到了和这个表一模一样的表,只是可能用了不同的语言去表达。所以我们应该抱着对算法先辈们的万分感激之情去使用这张宝贵的三角形表。
public static int[,] TriTable = new int[256, 16]
{
{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 8, 3, 9, 8, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 1, 2, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 2, 10, 0, 2, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 8, 3, 2, 10, 8, 10, 9, 8, -1, -1, -1, -1, -1, -1, -1},
{3, 11, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 11, 2, 8, 11, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 9, 0, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 11, 2, 1, 9, 11, 9, 8, 11, -1, -1, -1, -1, -1, -1, -1},
{3, 10, 1, 11, 10, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 10, 1, 0, 8, 10, 8, 11, 10, -1, -1, -1, -1, -1, -1, -1},
{3, 9, 0, 3, 11, 9, 11, 10, 9, -1, -1, -1, -1, -1, -1, -1},
{9, 8, 10, 10, 8, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 7, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 3, 0, 7, 3, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 1, 9, 4, 7, 1, 7, 3, 1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 4, 7, 3, 0, 4, 1, 2, 10, -1, -1, -1, -1, -1, -1, -1},
{9, 2, 10, 9, 0, 2, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1},
{2, 10, 9, 2, 9, 7, 2, 7, 3, 7, 9, 4, -1, -1, -1, -1},
{8, 4, 7, 3, 11, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 4, 7, 11, 2, 4, 2, 0, 4, -1, -1, -1, -1, -1, -1, -1},
{9, 0, 1, 8, 4, 7, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1},
{4, 7, 11, 9, 4, 11, 9, 11, 2, 9, 2, 1, -1, -1, -1, -1},
{3, 10, 1, 3, 11, 10, 7, 8, 4, -1, -1, -1, -1, -1, -1, -1},
{1, 11, 10, 1, 4, 11, 1, 0, 4, 7, 11, 4, -1, -1, -1, -1},
{4, 7, 8, 9, 0, 11, 9, 11, 10, 11, 0, 3, -1, -1, -1, -1},
{4, 7, 11, 4, 11, 9, 9, 11, 10, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 4, 0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 5, 4, 1, 5, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 5, 4, 8, 3, 5, 3, 1, 5, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 9, 5, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 8, 1, 2, 10, 4, 9, 5, -1, -1, -1, -1, -1, -1, -1},
{5, 2, 10, 5, 4, 2, 4, 0, 2, -1, -1, -1, -1, -1, -1, -1},
{2, 10, 5, 3, 2, 5, 3, 5, 4, 3, 4, 8, -1, -1, -1, -1},
{9, 5, 4, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 11, 2, 0, 8, 11, 4, 9, 5, -1, -1, -1, -1, -1, -1, -1},
{0, 5, 4, 0, 1, 5, 2, 3, 11, -1, -1, -1, -1, -1, -1, -1},
{2, 1, 5, 2, 5, 8, 2, 8, 11, 4, 8, 5, -1, -1, -1, -1},
{10, 3, 11, 10, 1, 3, 9, 5, 4, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 5, 0, 8, 1, 8, 10, 1, 8, 11, 10, -1, -1, -1, -1},
{5, 4, 0, 5, 0, 11, 5, 11, 10, 11, 0, 3, -1, -1, -1, -1},
{5, 4, 8, 5, 8, 10, 10, 8, 11, -1, -1, -1, -1, -1, -1, -1},
{9, 7, 8, 5, 7, 9, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 3, 0, 9, 5, 3, 5, 7, 3, -1, -1, -1, -1, -1, -1, -1},
{0, 7, 8, 0, 1, 7, 1, 5, 7, -1, -1, -1, -1, -1, -1, -1},
{1, 5, 3, 3, 5, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 7, 8, 9, 5, 7, 10, 1, 2, -1, -1, -1, -1, -1, -1, -1},
{10, 1, 2, 9, 5, 0, 5, 3, 0, 5, 7, 3, -1, -1, -1, -1},
{8, 0, 2, 8, 2, 5, 8, 5, 7, 10, 5, 2, -1, -1, -1, -1},
{2, 10, 5, 2, 5, 3, 3, 5, 7, -1, -1, -1, -1, -1, -1, -1},
{7, 9, 5, 7, 8, 9, 3, 11, 2, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 7, 9, 7, 2, 9, 2, 0, 2, 7, 11, -1, -1, -1, -1},
{2, 3, 11, 0, 1, 8, 1, 7, 8, 1, 5, 7, -1, -1, -1, -1},
{11, 2, 1, 11, 1, 7, 7, 1, 5, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 8, 8, 5, 7, 10, 1, 3, 10, 3, 11, -1, -1, -1, -1},
{5, 7, 0, 5, 0, 9, 7, 11, 0, 1, 0, 10, 11, 10, 0, -1},
{11, 10, 0, 11, 0, 3, 10, 5, 0, 8, 0, 7, 5, 7, 0, -1},
{11, 10, 5, 7, 11, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{10, 6, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 0, 1, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 8, 3, 1, 9, 8, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1},
{1, 6, 5, 2, 6, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 6, 5, 1, 2, 6, 3, 0, 8, -1, -1, -1, -1, -1, -1, -1},
{9, 6, 5, 9, 0, 6, 0, 2, 6, -1, -1, -1, -1, -1, -1, -1},
{5, 9, 8, 5, 8, 2, 5, 2, 6, 3, 2, 8, -1, -1, -1, -1},
{2, 3, 11, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 0, 8, 11, 2, 0, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, 2, 3, 11, 5, 10, 6, -1, -1, -1, -1, -1, -1, -1},
{5, 10, 6, 1, 9, 2, 9, 11, 2, 9, 8, 11, -1, -1, -1, -1},
{6, 3, 11, 6, 5, 3, 5, 1, 3, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 11, 0, 11, 5, 0, 5, 1, 5, 11, 6, -1, -1, -1, -1},
{3, 11, 6, 0, 3, 6, 0, 6, 5, 0, 5, 9, -1, -1, -1, -1},
{6, 5, 9, 6, 9, 11, 11, 9, 8, -1, -1, -1, -1, -1, -1, -1},
{5, 10, 6, 4, 7, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 3, 0, 4, 7, 3, 6, 5, 10, -1, -1, -1, -1, -1, -1, -1},
{1, 9, 0, 5, 10, 6, 8, 4, 7, -1, -1, -1, -1, -1, -1, -1},
{10, 6, 5, 1, 9, 7, 1, 7, 3, 7, 9, 4, -1, -1, -1, -1},
{6, 1, 2, 6, 5, 1, 4, 7, 8, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 5, 5, 2, 6, 3, 0, 4, 3, 4, 7, -1, -1, -1, -1},
{8, 4, 7, 9, 0, 5, 0, 6, 5, 0, 2, 6, -1, -1, -1, -1},
{7, 3, 9, 7, 9, 4, 3, 2, 9, 5, 9, 6, 2, 6, 9, -1},
{3, 11, 2, 7, 8, 4, 10, 6, 5, -1, -1, -1, -1, -1, -1, -1},
{5, 10, 6, 4, 7, 2, 4, 2, 0, 2, 7, 11, -1, -1, -1, -1},
{0, 1, 9, 4, 7, 8, 2, 3, 11, 5, 10, 6, -1, -1, -1, -1},
{9, 2, 1, 9, 11, 2, 9, 4, 11, 7, 11, 4, 5, 10, 6, -1},
{8, 4, 7, 3, 11, 5, 3, 5, 1, 5, 11, 6, -1, -1, -1, -1},
{5, 1, 11, 5, 11, 6, 1, 0, 11, 7, 11, 4, 0, 4, 11, -1},
{0, 5, 9, 0, 6, 5, 0, 3, 6, 11, 6, 3, 8, 4, 7, -1},
{6, 5, 9, 6, 9, 11, 4, 7, 9, 7, 11, 9, -1, -1, -1, -1},
{10, 4, 9, 6, 4, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 10, 6, 4, 9, 10, 0, 8, 3, -1, -1, -1, -1, -1, -1, -1},
{10, 0, 1, 10, 6, 0, 6, 4, 0, -1, -1, -1, -1, -1, -1, -1},
{8, 3, 1, 8, 1, 6, 8, 6, 4, 6, 1, 10, -1, -1, -1, -1},
{1, 4, 9, 1, 2, 4, 2, 6, 4, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 8, 1, 2, 9, 2, 4, 9, 2, 6, 4, -1, -1, -1, -1},
{0, 2, 4, 4, 2, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 3, 2, 8, 2, 4, 4, 2, 6, -1, -1, -1, -1, -1, -1, -1},
{10, 4, 9, 10, 6, 4, 11, 2, 3, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 2, 2, 8, 11, 4, 9, 10, 4, 10, 6, -1, -1, -1, -1},
{3, 11, 2, 0, 1, 6, 0, 6, 4, 6, 1, 10, -1, -1, -1, -1},
{6, 4, 1, 6, 1, 10, 4, 8, 1, 2, 1, 11, 8, 11, 1, -1},
{9, 6, 4, 9, 3, 6, 9, 1, 3, 11, 6, 3, -1, -1, -1, -1},
{8, 11, 1, 8, 1, 0, 11, 6, 1, 9, 1, 4, 6, 4, 1, -1},
{3, 11, 6, 3, 6, 0, 0, 6, 4, -1, -1, -1, -1, -1, -1, -1},
{6, 4, 8, 11, 6, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 10, 6, 7, 8, 10, 8, 9, 10, -1, -1, -1, -1, -1, -1, -1},
{0, 7, 3, 0, 10, 7, 0, 9, 10, 6, 7, 10, -1, -1, -1, -1},
{10, 6, 7, 1, 10, 7, 1, 7, 8, 1, 8, 0, -1, -1, -1, -1},
{10, 6, 7, 10, 7, 1, 1, 7, 3, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 6, 1, 6, 8, 1, 8, 9, 8, 6, 7, -1, -1, -1, -1},
{2, 6, 9, 2, 9, 1, 6, 7, 9, 0, 9, 3, 7, 3, 9, -1},
{7, 8, 0, 7, 0, 6, 6, 0, 2, -1, -1, -1, -1, -1, -1, -1},
{7, 3, 2, 6, 7, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 3, 11, 10, 6, 8, 10, 8, 9, 8, 6, 7, -1, -1, -1, -1},
{2, 0, 7, 2, 7, 11, 0, 9, 7, 6, 7, 10, 9, 10, 7, -1},
{1, 8, 0, 1, 7, 8, 1, 10, 7, 6, 7, 10, 2, 3, 11, -1},
{11, 2, 1, 11, 1, 7, 10, 6, 1, 6, 7, 1, -1, -1, -1, -1},
{8, 9, 6, 8, 6, 7, 9, 1, 6, 11, 6, 3, 1, 3, 6, -1},
{0, 9, 1, 11, 6, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 8, 0, 7, 0, 6, 3, 11, 0, 11, 6, 0, -1, -1, -1, -1},
{7, 11, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 6, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 8, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 9, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 1, 9, 8, 3, 1, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1},
{10, 1, 2, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 3, 0, 8, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1},
{2, 9, 0, 2, 10, 9, 6, 11, 7, -1, -1, -1, -1, -1, -1, -1},
{6, 11, 7, 2, 10, 3, 10, 8, 3, 10, 9, 8, -1, -1, -1, -1},
{7, 2, 3, 6, 2, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{7, 0, 8, 7, 6, 0, 6, 2, 0, -1, -1, -1, -1, -1, -1, -1},
{2, 7, 6, 2, 3, 7, 0, 1, 9, -1, -1, -1, -1, -1, -1, -1},
{1, 6, 2, 1, 8, 6, 1, 9, 8, 8, 7, 6, -1, -1, -1, -1},
{10, 7, 6, 10, 1, 7, 1, 3, 7, -1, -1, -1, -1, -1, -1, -1},
{10, 7, 6, 1, 7, 10, 1, 8, 7, 1, 0, 8, -1, -1, -1, -1},
{0, 3, 7, 0, 7, 10, 0, 10, 9, 6, 10, 7, -1, -1, -1, -1},
{7, 6, 10, 7, 10, 8, 8, 10, 9, -1, -1, -1, -1, -1, -1, -1},
{6, 8, 4, 11, 8, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 6, 11, 3, 0, 6, 0, 4, 6, -1, -1, -1, -1, -1, -1, -1},
{8, 6, 11, 8, 4, 6, 9, 0, 1, -1, -1, -1, -1, -1, -1, -1},
{9, 4, 6, 9, 6, 3, 9, 3, 1, 11, 3, 6, -1, -1, -1, -1},
{6, 8, 4, 6, 11, 8, 2, 10, 1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 3, 0, 11, 0, 6, 11, 0, 4, 6, -1, -1, -1, -1},
{4, 11, 8, 4, 6, 11, 0, 2, 9, 2, 10, 9, -1, -1, -1, -1},
{10, 9, 3, 10, 3, 2, 9, 4, 3, 11, 3, 6, 4, 6, 3, -1},
{8, 2, 3, 8, 4, 2, 4, 6, 2, -1, -1, -1, -1, -1, -1, -1},
{0, 4, 2, 4, 6, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 9, 0, 2, 3, 4, 2, 4, 6, 4, 3, 8, -1, -1, -1, -1},
{1, 9, 4, 1, 4, 2, 2, 4, 6, -1, -1, -1, -1, -1, -1, -1},
{8, 1, 3, 8, 6, 1, 8, 4, 6, 6, 10, 1, -1, -1, -1, -1},
{10, 1, 0, 10, 0, 6, 6, 0, 4, -1, -1, -1, -1, -1, -1, -1},
{4, 6, 3, 4, 3, 8, 6, 10, 3, 0, 3, 9, 10, 9, 3, -1},
{10, 9, 4, 6, 10, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 5, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 4, 9, 5, 11, 7, 6, -1, -1, -1, -1, -1, -1, -1},
{5, 0, 1, 5, 4, 0, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1},
{11, 7, 6, 8, 3, 4, 3, 5, 4, 3, 1, 5, -1, -1, -1, -1},
{9, 5, 4, 10, 1, 2, 7, 6, 11, -1, -1, -1, -1, -1, -1, -1},
{6, 11, 7, 1, 2, 10, 0, 8, 3, 4, 9, 5, -1, -1, -1, -1},
{7, 6, 11, 5, 4, 10, 4, 2, 10, 4, 0, 2, -1, -1, -1, -1},
{3, 4, 8, 3, 5, 4, 3, 2, 5, 10, 5, 2, 11, 7, 6, -1},
{7, 2, 3, 7, 6, 2, 5, 4, 9, -1, -1, -1, -1, -1, -1, -1},
{9, 5, 4, 0, 8, 6, 0, 6, 2, 6, 8, 7, -1, -1, -1, -1},
{3, 6, 2, 3, 7, 6, 1, 5, 0, 5, 4, 0, -1, -1, -1, -1},
{6, 2, 8, 6, 8, 7, 2, 1, 8, 4, 8, 5, 1, 5, 8, -1},
{9, 5, 4, 10, 1, 6, 1, 7, 6, 1, 3, 7, -1, -1, -1, -1},
{1, 6, 10, 1, 7, 6, 1, 0, 7, 8, 7, 0, 9, 5, 4, -1},
{4, 0, 10, 4, 10, 5, 0, 3, 10, 6, 10, 7, 3, 7, 10, -1},
{7, 6, 10, 7, 10, 8, 5, 4, 10, 4, 8, 10, -1, -1, -1, -1},
{6, 9, 5, 6, 11, 9, 11, 8, 9, -1, -1, -1, -1, -1, -1, -1},
{3, 6, 11, 0, 6, 3, 0, 5, 6, 0, 9, 5, -1, -1, -1, -1},
{0, 11, 8, 0, 5, 11, 0, 1, 5, 5, 6, 11, -1, -1, -1, -1},
{6, 11, 3, 6, 3, 5, 5, 3, 1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 10, 9, 5, 11, 9, 11, 8, 11, 5, 6, -1, -1, -1, -1},
{0, 11, 3, 0, 6, 11, 0, 9, 6, 5, 6, 9, 1, 2, 10, -1},
{11, 8, 5, 11, 5, 6, 8, 0, 5, 10, 5, 2, 0, 2, 5, -1},
{6, 11, 3, 6, 3, 5, 2, 10, 3, 10, 5, 3, -1, -1, -1, -1},
{5, 8, 9, 5, 2, 8, 5, 6, 2, 3, 8, 2, -1, -1, -1, -1},
{9, 5, 6, 9, 6, 0, 0, 6, 2, -1, -1, -1, -1, -1, -1, -1},
{1, 5, 8, 1, 8, 0, 5, 6, 8, 3, 8, 2, 6, 2, 8, -1},
{1, 5, 6, 2, 1, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 3, 6, 1, 6, 10, 3, 8, 6, 5, 6, 9, 8, 9, 6, -1},
{10, 1, 0, 10, 0, 6, 9, 5, 0, 5, 6, 0, -1, -1, -1, -1},
{0, 3, 8, 5, 6, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{10, 5, 6, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 5, 10, 7, 5, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{11, 5, 10, 11, 7, 5, 8, 3, 0, -1, -1, -1, -1, -1, -1, -1},
{5, 11, 7, 5, 10, 11, 1, 9, 0, -1, -1, -1, -1, -1, -1, -1},
{10, 7, 5, 10, 11, 7, 9, 8, 1, 8, 3, 1, -1, -1, -1, -1},
{11, 1, 2, 11, 7, 1, 7, 5, 1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 1, 2, 7, 1, 7, 5, 7, 2, 11, -1, -1, -1, -1},
{9, 7, 5, 9, 2, 7, 9, 0, 2, 2, 11, 7, -1, -1, -1, -1},
{7, 5, 2, 7, 2, 11, 5, 9, 2, 3, 2, 8, 9, 8, 2, -1},
{2, 5, 10, 2, 3, 5, 3, 7, 5, -1, -1, -1, -1, -1, -1, -1},
{8, 2, 0, 8, 5, 2, 8, 7, 5, 10, 2, 5, -1, -1, -1, -1},
{9, 0, 1, 5, 10, 3, 5, 3, 7, 3, 10, 2, -1, -1, -1, -1},
{9, 8, 2, 9, 2, 1, 8, 7, 2, 10, 2, 5, 7, 5, 2, -1},
{1, 3, 5, 3, 7, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 7, 0, 7, 1, 1, 7, 5, -1, -1, -1, -1, -1, -1, -1},
{9, 0, 3, 9, 3, 5, 5, 3, 7, -1, -1, -1, -1, -1, -1, -1},
{9, 8, 7, 5, 9, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{5, 8, 4, 5, 10, 8, 10, 11, 8, -1, -1, -1, -1, -1, -1, -1},
{5, 0, 4, 5, 11, 0, 5, 10, 11, 11, 3, 0, -1, -1, -1, -1},
{0, 1, 9, 8, 4, 10, 8, 10, 11, 10, 4, 5, -1, -1, -1, -1},
{10, 11, 4, 10, 4, 5, 11, 3, 4, 9, 4, 1, 3, 1, 4, -1},
{2, 5, 1, 2, 8, 5, 2, 11, 8, 4, 5, 8, -1, -1, -1, -1},
{0, 4, 11, 0, 11, 3, 4, 5, 11, 2, 11, 1, 5, 1, 11, -1},
{0, 2, 5, 0, 5, 9, 2, 11, 5, 4, 5, 8, 11, 8, 5, -1},
{9, 4, 5, 2, 11, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 5, 10, 3, 5, 2, 3, 4, 5, 3, 8, 4, -1, -1, -1, -1},
{5, 10, 2, 5, 2, 4, 4, 2, 0, -1, -1, -1, -1, -1, -1, -1},
{3, 10, 2, 3, 5, 10, 3, 8, 5, 4, 5, 8, 0, 1, 9, -1},
{5, 10, 2, 5, 2, 4, 1, 9, 2, 9, 4, 2, -1, -1, -1, -1},
{8, 4, 5, 8, 5, 3, 3, 5, 1, -1, -1, -1, -1, -1, -1, -1},
{0, 4, 5, 1, 0, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{8, 4, 5, 8, 5, 3, 9, 0, 5, 0, 3, 5, -1, -1, -1, -1},
{9, 4, 5, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 11, 7, 4, 9, 11, 9, 10, 11, -1, -1, -1, -1, -1, -1, -1},
{0, 8, 3, 4, 9, 7, 9, 11, 7, 9, 10, 11, -1, -1, -1, -1},
{1, 10, 11, 1, 11, 4, 1, 4, 0, 7, 4, 11, -1, -1, -1, -1},
{3, 1, 4, 3, 4, 8, 1, 10, 4, 7, 4, 11, 10, 11, 4, -1},
{4, 11, 7, 9, 11, 4, 9, 2, 11, 9, 1, 2, -1, -1, -1, -1},
{9, 7, 4, 9, 11, 7, 9, 1, 11, 2, 11, 1, 0, 8, 3, -1},
{11, 7, 4, 11, 4, 2, 2, 4, 0, -1, -1, -1, -1, -1, -1, -1},
{11, 7, 4, 11, 4, 2, 8, 3, 4, 3, 2, 4, -1, -1, -1, -1},
{2, 9, 10, 2, 7, 9, 2, 3, 7, 7, 4, 9, -1, -1, -1, -1},
{9, 10, 7, 9, 7, 4, 10, 2, 7, 8, 7, 0, 2, 0, 7, -1},
{3, 7, 10, 3, 10, 2, 7, 4, 10, 1, 10, 0, 4, 0, 10, -1},
{1, 10, 2, 8, 7, 4, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 1, 4, 1, 7, 7, 1, 3, -1, -1, -1, -1, -1, -1, -1},
{4, 9, 1, 4, 1, 7, 0, 8, 1, 8, 7, 1, -1, -1, -1, -1},
{4, 0, 3, 7, 4, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{4, 8, 7, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{9, 10, 8, 10, 11, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 9, 3, 9, 11, 11, 9, 10, -1, -1, -1, -1, -1, -1, -1},
{0, 1, 10, 0, 10, 8, 8, 10, 11, -1, -1, -1, -1, -1, -1, -1},
{3, 1, 10, 11, 3, 10, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 2, 11, 1, 11, 9, 9, 11, 8, -1, -1, -1, -1, -1, -1, -1},
{3, 0, 9, 3, 9, 11, 1, 2, 9, 2, 11, 9, -1, -1, -1, -1},
{0, 2, 11, 8, 0, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{3, 2, 11, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 3, 8, 2, 8, 10, 10, 8, 9, -1, -1, -1, -1, -1, -1, -1},
{9, 10, 2, 0, 9, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{2, 3, 8, 2, 8, 10, 0, 1, 8, 1, 10, 8, -1, -1, -1, -1},
{1, 10, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{1, 3, 8, 9, 1, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 9, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{0, 3, 8, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1},
{-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1}
};
我们可以看出TriTable是一个256*16的二维数组,每行对应一个体元配置,行内有16个数,每三个数为一组,代表一个三角形,-1代表无效值。之所以设16个位置是因为部分配置可能最多包含5个三角形片,那么就会占到5*3=15个空位,最后一个填-1代表结束的标记。那么,有了这张表,任何一种体元配置都可以方便的找出里面三角形片的结构。注意这张表里使用的边索引以及对应的顶点索引都是和本文上文所列的表中的编号是对应上的。也就是说,像本文这样对顶点和编进行编号是使用这张表的必要条件。利用这张表实现MC算法,不仅要有这张表的内容,还必须有正确的体素和边的编号顺序,也就是上文所谈到的顶点和边的编号表中的顺序。
那么这样可以推导出从一个体元中抽取三角形片的主要逻辑思路如下:
- 对于体元C,根据其8个体素的像素值确定其体元配置V
- 根据体元配置V,获取三角形表中第V行的数组A
- 假如A[0]不为-1,则说明此体元为边界体元,其中必有三角片,则每三个数一组,获取三角形顶点所在边的索引,假设获取到了N组。
- 对这N组边索引:
- 对每组边索引e0、e1、e2根据编号分别找出其两端点(e0p0,e0p1)、(e1p0,e1p1)、(e2p0,e2p1)
- 根据两端点坐标计算出每个边上的插值点坐标e0pm、e1pm、e2pm
- 以此三点组成三角形
- 返回构建的N个三角形
了解了在每个体元中如何抽取三角形,则就很容易理解MC算法的主要逻辑了。MC算法本质就是遍历所有的体元,找出其中的三角片最后集合起来组成图像中实点表面的三角网格(Mesh)。
For(layerIndex k from 0 ~depth-1)
For(columnIndex j from 0 ~height-1)
For(rowIndex i from 0 ~width-1)
Build Cube At (i,j,k)
Extract Triangles from The Cube
下面介绍如何使用C#语言实现本算法,首先实现本算法利用了前面几篇所采用的一些类。
Bitmap3d类:
public class BitMap3d
{
public const byte WHITE = 255;
public const byte BLACK = 0;
public byte[] data;
public int width;
public int height;
public int depth;
public BitMap3d(int width, int height, int depth, byte v)
{
this.width = width;
this.height = height;
this.depth = depth;
data = new byte[width * height * depth];
for (int i = 0; i < width * height * depth; i++)
data[i] = v;
}
public BitMap3d(byte[] data, int width, int height, int depth)
{
this.data = data;
this.width = width;
this.height = height;
this.depth = depth;
}
public void SetPixel(int x, int y, int z, byte v)
{
data[x + y * width + z * width * height] = v;
}
public byte GetPixel(int x, int y, int z)
{
return data[x + y * width + z * width * height];
}
public void ReadRaw(string path)
{
FileStream fs = new FileStream(path, FileMode.Open, FileAccess.Read);
fs.Read(data, 0, width * height * depth);
fs.Close();
}
}
Mesh类:
public struct Point3d
{
public float X;
public float Y;
public float Z;
public Point3d(float x, float y, float z)
{
X = x;
Y = y;
Z = z;
}
}
public struct Triangle
{
public int P0Index;
public int P1Index;
public int P2Index;
public Triangle(int p0index, int p1index, int p2index)
{
P0Index = p0index;
P1Index = p1index;
P2Index = p2index;
}
}
public class Mesh
{
public List<Point3d> Vertices = null;
public List<Triangle> Faces = null;
public Mesh()
{
Vertices = new List<Point3d>();
Faces = new List<Triangle>();
}
public int AddVertex(Point3d toAdd)
{
int index = Vertices.Count;
Vertices.Add(toAdd);
return index;
}
public int AddFace(Triangle tri)
{
int index = Faces.Count;
Faces.Add(tri);
return index;
}
public void Clear()
{
Vertices.Clear();
Faces.Clear();
}
}
用于输出PLY网格文件的类
public class PlyManager
{
private static void AWriteV(StreamWriter sw, double v1, double v2, double v3, byte r, byte g, byte b)
{
int r1 = (int)r;
int g1 = (int)g;
int b1 = (int)b;
sw.Write(string.Format("{0} {1} {2} {3} {4} {5}\n", v1.ToString("0.0"), v2.ToString("0.0"), v3.ToString("0.0"), r1, g1, b1));
}
private static void AWriteF(StreamWriter sw, int i1, int i2, int i3)
{
sw.Write(string.Format("{0} {1} {2} {3}\n", 3, i1, i2, i3));
}
public static void Output(Mesh mesh, string filePath)
{
FileStream fs = new FileStream(filePath, FileMode.Create);
StreamWriter sw = new StreamWriter(fs, Encoding.Default);
sw.Write("ply\n");
sw.Write("format ascii 1.0\n");
sw.Write("comment VCGLIB generated\n");
sw.Write(string.Format("element vertex {0}\n", mesh.Vertices.Count));
sw.Write("property float x\n");
sw.Write("property float y\n");
sw.Write("property float z\n");
sw.Write("property uchar red\n");
sw.Write("property uchar green\n");
sw.Write("property uchar blue\n");
sw.Write(string.Format("element face {0}\n", mesh.Faces.Count));
sw.Write("property list int int vertex_indices\n");
sw.Write("end_header\n");
for (int i = 0; i < mesh.Vertices.Count; i++)
{
AWriteV(sw, mesh.Vertices[i].X, mesh.Vertices[i].Y, mesh.Vertices[i].Z, 255, 255, 255);
}
for (int i = 0; i < mesh.Faces.Count; i++)
{
AWriteF(sw, mesh.Faces[i].P0Index, mesh.Faces[i].P1Index, mesh.Faces[i].P2Index);
}
sw.Close();
fs.Close();
}
}
用于实现顶点焊接的MeshBuilder类,内部采用哈希表来焊接顶点:
class MeshBuilder_FloatVertex
{
Mesh mesh;
Dictionary<Point3d, int> hashMap;
public MeshBuilder_FloatVertex(int width, int height, int depth)
{
mesh = new Mesh();
this.hashMap = new Dictionary<Point3d, int>();
}
public void AddTriangle(Point3d p0,Point3d p1,Point3d p2)
{
int p0i;
int p1i;
int p2i;
int index = 0;
bool hasValue;
hasValue = hashMap.ContainsKey(p0);
if (!hasValue)
{
p0i = mesh.AddVertex(p0);
hashMap.Add(p0,p0i);
}
else
{
index = hashMap[p0];
p0i = index;
} hasValue = hashMap.ContainsKey(p1);
if (!hasValue)
{
p1i = mesh.AddVertex(p1);
hashMap.Add(p1,p1i);
}
else
{
index = hashMap[p1];
p1i = index;
} hasValue = hashMap.ContainsKey(p2);
if (!hasValue)
{
p2i = mesh.AddVertex(p2);
hashMap.Add(p2, p2i);
}
else
{
index = hashMap[p2];
p2i = index;
}
Triangle t = new Triangle(p0i, p1i, p2i);
mesh.AddFace(t);
}
public Mesh GetMesh()
{
return mesh;
}
public void Clear()
{
hashMap.Clear();
}
}
然后是MCProcesser的实现,首先要定义Cube类,在Cube类中定义了一些静态的数据,用于快速查找体素和边对应的信息:
struct Int16Triple
{
public int X;
public int Y;
public int Z;
public Int16Triple(int x, int y, int z)
{
X = x;
Y = y;
Z = z;
}
}
class Cube
{
public static byte VULF = 1 << 0;
public static byte VULB = 1 << 1;
public static byte VLLB = 1 << 2;
public static byte VLLF = 1 << 3;
public static byte VURF = 1 << 4;
public static byte VURB = 1 << 5;
public static byte VLRB = 1 << 6;
public static byte VLRF = 1 << 7;
//以上为体素为实点的位标记
public static Int16Triple[] PointIndexToPointDelta = new Int16Triple[8]
{
new Int16Triple(0, 1, 1 ),
new Int16Triple(0, 1, 0 ),
new Int16Triple(0, 0, 0 ),
new Int16Triple(0, 0, 1 ),
new Int16Triple(1, 1, 1 ),
new Int16Triple(1, 1, 0 ),
new Int16Triple(1, 0, 0 ),
new Int16Triple(1, 0, 1 )
};//体元内每个体素相对基准体素坐标的偏移
public static byte[] PointIndexToFlag=new byte[8]
{
VULF,
VULB,
VLLB,
VLLF,
VURF,
VURB,
VLRB,
VLRF
};//每个体素对应的位标记
public static int[,] EdgeIndexToEdgeVertexIndex = new int[12, 2]
{
{0,1}, {1,2},
{2,3},{3,0},
{4,5},{5,6},
{6,7}, {7,4},
{0,4}, {1,5},
{2,6}, {3,7}
};//每个边对应的两顶点体素的索引
public int CellIndexX;
public int CellIndexY;
public int CellIndexZ;
public Cube(int cellIndexX, int cellIndexY, int cellIndexZ)
{
this.CellIndexX = cellIndexX;
this.CellIndexY = cellIndexY;
this.CellIndexZ = cellIndexZ;
for (int i = 0; i < 8; i++)
{
cubeImageIndices[i].X = cellIndexX + PointIndexToPointDelta[i].X;
cubeImageIndices[i].Y = cellIndexY + PointIndexToPointDelta[i].Y;
cubeImageIndices[i].Z = cellIndexZ + PointIndexToPointDelta[i].Z;
}
}//使用基准体素坐标初始化Cube
public Int16Triple[] cubeImageIndices = new Int16Triple[8];//用于存储8个体素的坐标
}
MC算法实现主体类:
class MCProcessor
{
BitMap3d bmp;
public MCProcessor(BitMap3d bitmap)
{
this.bmp = bitmap;
}
public virtual bool IsInside(int x, int y, int z)
{
if (x <= 0 || y <= 0 || z <= 0 || x > bmp.width || y > bmp.height || z > bmp.depth)
return false;
else
{
return bmp.GetPixel(x, y, z) == BitMap3d.WHITE;
}
}//judge if a voxel is inside the surface
public Mesh GeneratorSurface()
{
MeshBuilder_FloatVertex builder = new MeshBuilder_FloatVertex(bmp.width + 2, bmp.height + 2, bmp.depth + 2);// this class can build mesh from independent triangles
for (int k = 0; k < bmp.depth - 1; k++)
{
for (int j = 0; j < bmp.height - 1; j++)
{
for (int i = 0; i < bmp.width - 1; i++)
{
Cube cell = new Cube(i, j, k);//builde Cube for Cell at i j k
byte config = GetConfig(ref cell);// get byte config for the cell
ExtractTriangles(ref cell, config, builder);// extract triangles from cell and push into
}
}
}
return builder.GetMesh();
}
private byte GetConfig(ref Cube cube)
{
byte value = 0;
for (int i = 0; i < 8; i++)
{
if (IsInside(cube.cubeImageIndices[i].X, cube.cubeImageIndices[i].Y, cube.cubeImageIndices[i].Z))
{
value |= Cube.PointIndexToFlag[i];
}
}
return value;
}//get copnfig
private void ExtractTriangles(ref Cube cube, byte value, MeshBuilder_FloatVertex builder)
{
if (MCTable.TriTable[value, 0] != -1)
{
int index = 0;
while (MCTable.TriTable[value, index] != -1)
{
int e0index = MCTable.TriTable[value, index];
int e1index = MCTable.TriTable[value, index + 1];
int e2index = MCTable.TriTable[value, index + 2]; Int16Triple e0p0 = cube.cubeImageIndices[Cube.EdgeIndexToEdgeVertexIndex[e0index, 0]];
Int16Triple e0p1 = cube.cubeImageIndices[Cube.EdgeIndexToEdgeVertexIndex[e0index, 1]]; Int16Triple e1p0 = cube.cubeImageIndices[Cube.EdgeIndexToEdgeVertexIndex[e1index, 0]];
Int16Triple e1p1 = cube.cubeImageIndices[Cube.EdgeIndexToEdgeVertexIndex[e1index, 1]]; Int16Triple e2p0 = cube.cubeImageIndices[Cube.EdgeIndexToEdgeVertexIndex[e2index, 0]];
Int16Triple e2p1 = cube.cubeImageIndices[Cube.EdgeIndexToEdgeVertexIndex[e2index, 1]]; Point3d e0pm = GetIntersetedPoint(e0p0, e0p1);
Point3d e1pm = GetIntersetedPoint(e1p0, e1p1);
Point3d e2pm = GetIntersetedPoint(e2p0, e2p1); builder.AddTriangle(e0pm, e1pm, e2pm); index += 3;
}
}
}//extract triangles and put them into mesh builder private Point3d GetIntersetedPoint(Int16Triple p0, Int16Triple p1)
{
return new Point3d((p0.X + p1.X) / 2.0f, (p0.Y + p1.Y) / 2.0f, (p0.Z + p1.Z) / 2.0f);
}//findInterseted point
}
算法结果预览
测试数据采用Lobester.raw 选取体素值在27~255之间的体素作为内容。其余部分为背景,采用上述算法生成的Mesh的PLY文件,一共有162060个点和324296个三角形。
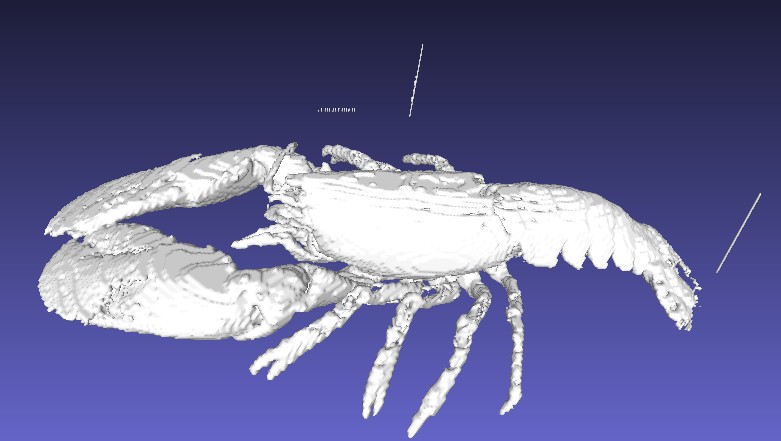 |
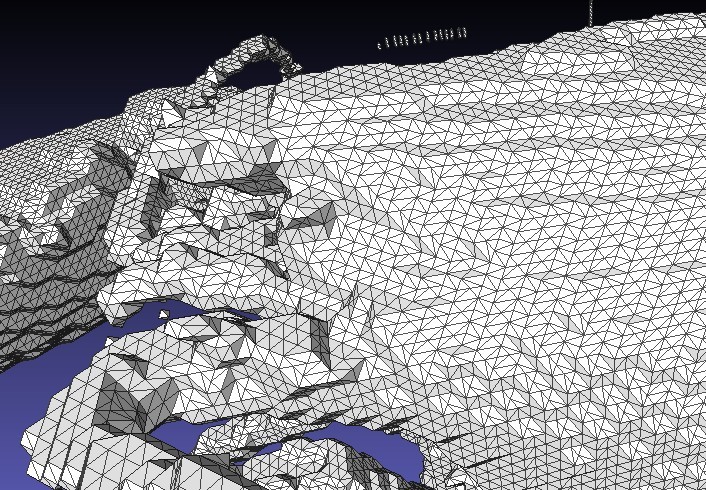 |
| 渲染图 | 网格图(放大了) |
与MC经典算法的区别
必须指出的是本文遍历体元抽取三角形的算法本质思想与经典MC算法是统一的,但是经典的MC算法在最初的论文里的实现方式与本文介绍的方式有所区别,本文为了便于理解简化了一些细节操作。例如论文中的经典算法在遍历图像时,是以层为单位来遍历体素,这样能够减少体素的访问次数,同时经典论文生成的是针对某个值的等值面,因而在计算插值点时采用了体素值权值来确定插值的位置,而本文简化这一过程,直接采用边中点作为插值点。同时经典算法不包括顶点焊接的过程。
下一篇会基于本篇介绍的内容,介绍一个简化的利用MC思想实现的网格生成的SMC算法。两个算法共同维护于:https://github.com/chnhideyoshi/SeededGrow2d/tree/master/SMC。其中在博文”基于八叉树的网格生成算法剖析“中还有一部分MC与SMC的实现代码在:https://github.com/chnhideyoshi/OctreeBaseSimplifiedMarchingCubes中
(博主注:采用更高效的哈希表实现MC算法的文章以及代码参见”一种适合于MC与SMC算法的哈希表设计“)。
爬网的太疯狂了,转载本文要注明出处啊:http://www.cnblogs.com/chnhideyoshi/
图像数据到网格数据-1——Marching Cubes算法的一种实现的更多相关文章
- 图像数据到网格数据-2——改进的SMC算法的实现
概要 本篇接上一篇继续介绍网格生成算法,同时不少内容继承自上篇.上篇介绍了经典的三维图像网格生成算法MarchingCubes,并且基于其思想和三角形表实现了对样例数据的网格构建.本篇继续探讨网格生成 ...
- 图像数据到网格数据-1——MarchingCubes算法
原文:http://blog.csdn.net/u013339596/article/details/19167907 概述 之前的博文已经完整的介绍了三维图像数据和三角形网格数据.在实际应用中,利用 ...
- 图像数据到网格数据-3——实现Cuberille算法
前言 这是本博客网格生成算法系列的第三篇,第一篇里面介绍了最为流行的MarchingCubes算法,第二篇中使用新三角形表来对MC算法进行了简化改进,形成了SMC算法.而这篇将介绍一种新的不同与MC算 ...
- 水泡动画模拟(Marching Cubes)
Marching Cubes算法是三维离散数据场中提取等值面的经典算法,其主要应用于医学领域的可视化场景,例如CT扫描和MRI扫描的3D重建等. 算法主要的思想是在三维离散数据场中通过线性插值来逼近等 ...
- CUDA 实现JPEG图像解码为RGB数据
了解JPEG数据格式的人应该easy想到.其对图像以8*8像素块大小进行切割压缩的方法非常好用并行处理的思想来实现.而其实英伟达的CUDA自v5.5開始也提供了JPEG编解码的演示样例.该演示样例存储 ...
- KubeCon 2021|使用 eBPF 代替 iptables 优化服务网格数据面性能
作者 刘旭,腾讯云高级工程师,专注容器云原生领域,有多年大规模 Kubernetes 集群管理及微服务治理经验,现负责腾讯云服务网格 TCM 数据面产品架构设计和研发工作. 引言 目前以 Istio[ ...
- Marching squares & Marching cubes
提要 Marching squares 主要是用于从一个地图(用二维数组表示)生成轮廓的算法.Marching cubes则相应的是在空间生成网格的方法.最常见的应用就是天气预报中气压图的生成.还经常 ...
- 北京市行政村边界shp数据/北京市乡镇边界/北京市土地利用分类数据/北京市气象数据/降雨量分布数据/太阳辐射数据
数据下载链接:数据下载链接 北京是一座有着三千多年历史的古都,在不同的朝代有着不同的称谓,大致算起来有二十多个别称.北京地势西北高.东南低.西部.北部和东北部三面环山,东南部是一片缓缓向渤海倾斜的 ...
- 广西省行政村边界shp数据/广西省乡镇边界/广西省土地利用分类数据/广西省气象数据/降雨量分布数据/太阳辐射数据
数据下载链接:数据下载链接 广西壮族自治区,地处中国南部,北回归线横贯中部,属亚热带季风气候区.南北以贺州--东兰一线为界,此界以北属中亚热带季风气候区,以南属南亚热带季风气候区. 数据范围:全 ...
随机推荐
- OC-封装,继承,多态
主要内容概括 标号 主题 内容 一 封装 面向对象三大特性;封装的概念/原因/好处/原则 二 *getter和setter setter / getter方法;注意点 三 自定义代码段 如何自定义代码 ...
- 【Linux】【Services】【Docker】应用
1. Docker应用: 镜像:包含了启动Docker容器所需要的文件系统层级及其内容:基于UnionFS采用分层结构实现: bootfs,rootfs registry:保存docker镜像及镜像层 ...
- 前端两大框架 vue 和 react 的区别
1. 设计思想 vue: vue的官网介绍说vue是一种渐进式框架,采用自底向上增量开发的设计: react: 采用函数式编程,推崇纯组件,数据不可变,单向数据流: 2. 编写语法 vue: 采用单文 ...
- windows 查看端口被占用,解除占用
查看 (列举端口为2688) netstat -ano | findstr "2688" 解除 原文地址
- 【JavaWeb】【Maven】001 下载与配置
Maven下载与配置 Download Url:Maven – Download Apache Maven After downloading it, unpack it and configure ...
- 1、Spring简介及IOC入门案例
一.Spring框架介绍 1.介绍 Spring框架是由于软件开发的复杂性而创建的.Spring使用的是基本的JavaBean来完成以前只可能由EJB完成的事情.然而,Spring的用途不仅仅限于服务 ...
- 控制 Python 类的序列化过程
问题 有的类是不支持在多进程间传递的,如果非要这么做,可能会引发奇怪的现象.比如下面这段代码: from concurrent.futures import ProcessPoolExecutor, ...
- 使用批处理文件(.bat)启动多个CMD窗口并执行命令
由于每次启动本机的kafka都需要打开2个cmd窗口,分别启动zookeeper服务和kafka服务,操作相对繁琐,于是想起了批处理来帮忙一键启动. 在桌面新建一个txt文件,改后缀名为.bat,并加 ...
- LuoguP7784 [AC6-M15] “大吊灯”攻略作战 题解
Content 你要把 \(n\times m\) 的一个矩阵划分成若干个矩阵,使得对于每一个矩阵: 不存在两个矩阵合起来是一个矩阵. 划分的矩阵个数不超过 \(10\). 请给出一个划分方案,或者报 ...
- 谷歌浏览器请求返回JSON内容自动格式化
我们使用谷歌浏览器的扩展插件 下载插件 官方网址:https://github.com/gildas-lormeau/JSONView-for-Chrome 我也上传了 一份:https://yvio ...
