【UE4】GAMES101 图形学作业3：Blinn-Phong 模型与着色

总览

• 在这次编程任务中，我们会进一步模拟现代图形技术。我们在代码中添加了Object Loader(用于加载三维模型), Vertex Shader 与Fragment Shader，并且支持了纹理映射。
• 而在本次实验中，你需要完成的任务是:
  1. 修改函数rasterize_triangle(const Triangle& t) in rasterizer.cpp:
     
     在此处实现与作业2 类似的插值算法，实现法向量、颜色、纹理颜色的插值。
  2. 修改函数get_projection_matrix() in main.cpp:
     
     将你自己在之前的实验中实现的投影矩阵填到此处，此时你可以运行./Rasterizer output.png normal来观察法向量实现结果。
  3. 修改函数phong_fragment_shader() in main.cpp:
     
     实现Blinn-Phong 模型计算Fragment Color.
  4. 修改函数texture_fragment_shader() in main.cpp:
     
     在实现 Blinn-Phong 的基础上，将纹理颜色视为公式中的kd，实现Texture Shading FragmentShader.
  5. 修改函数bump_fragment_shader() in main.cpp:
     
     在实现 Blinn-Phong 的基础上，仔细阅读该函数中的注释，实现Bump mapping.
  6. 修改函数displacement_fragment_shader() in main.cpp:
     
     在实现Bump mapping 的基础上，实现displacement mapping.

实现

直接在UE4用材质实现。

normal shader

• 材质代码

  

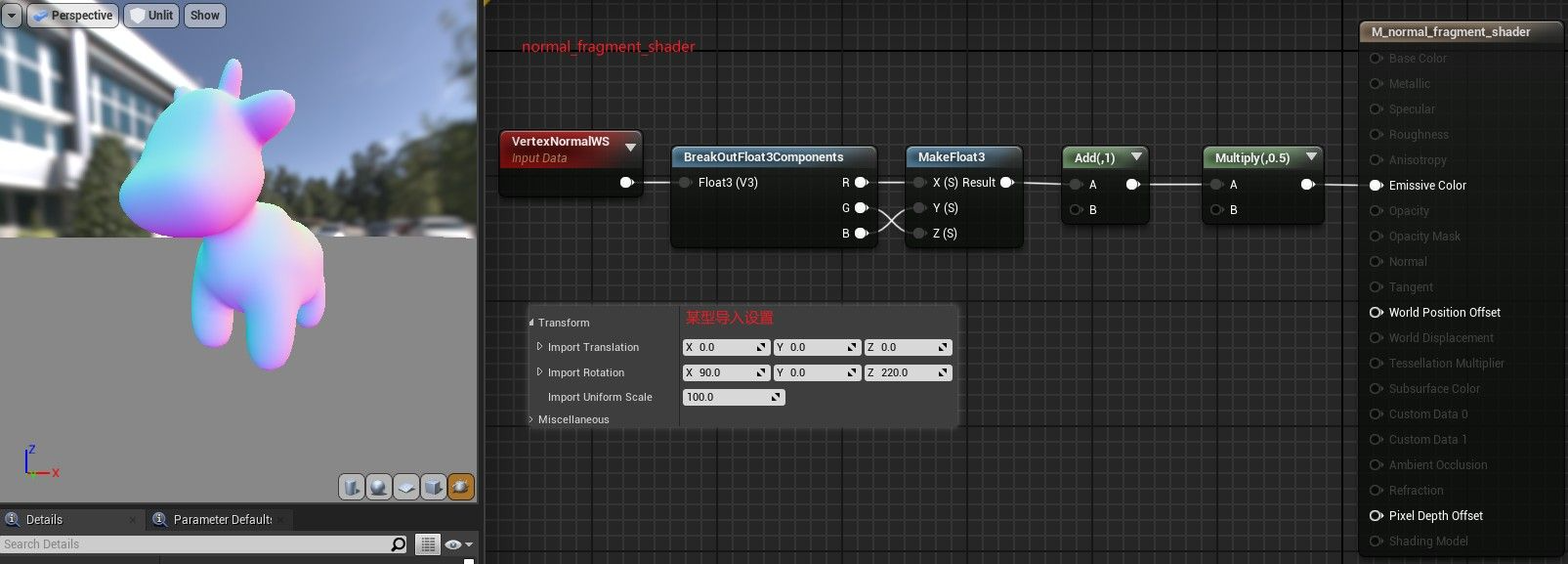
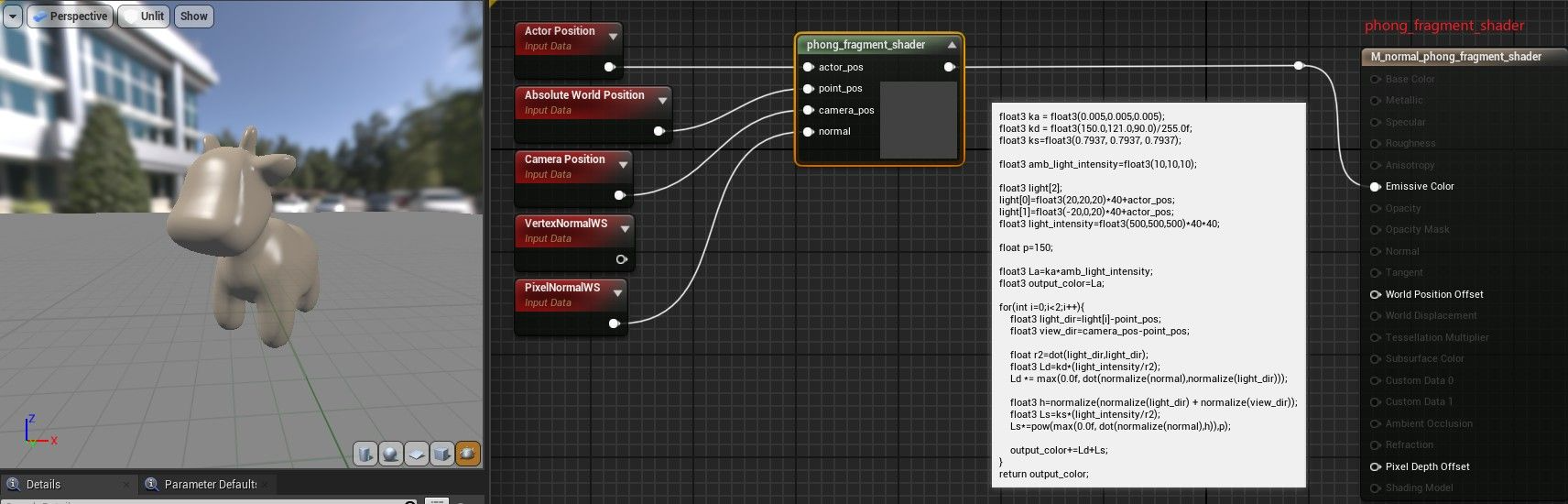
Blinn-phong模型 phong_fragment_shader

• 计算公式

  

• HLSL 代码

  • 注意模型放大后，相应系数也应该放大

  

Blinn-Phong模型 texture_fragment_shader

• 在 phong_fragment_shader 的基础上，将 kd 改为贴图输入

• HLSL 代码

  

Blinn-Phong模型 texture_fragment_shader （双线性插值）

• 先水平方向上插值，再垂直方向上插值

  

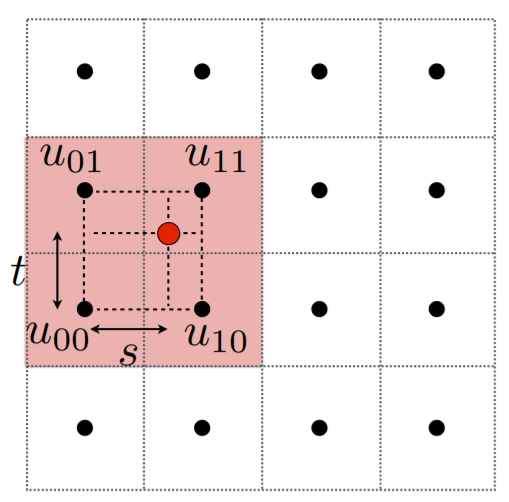
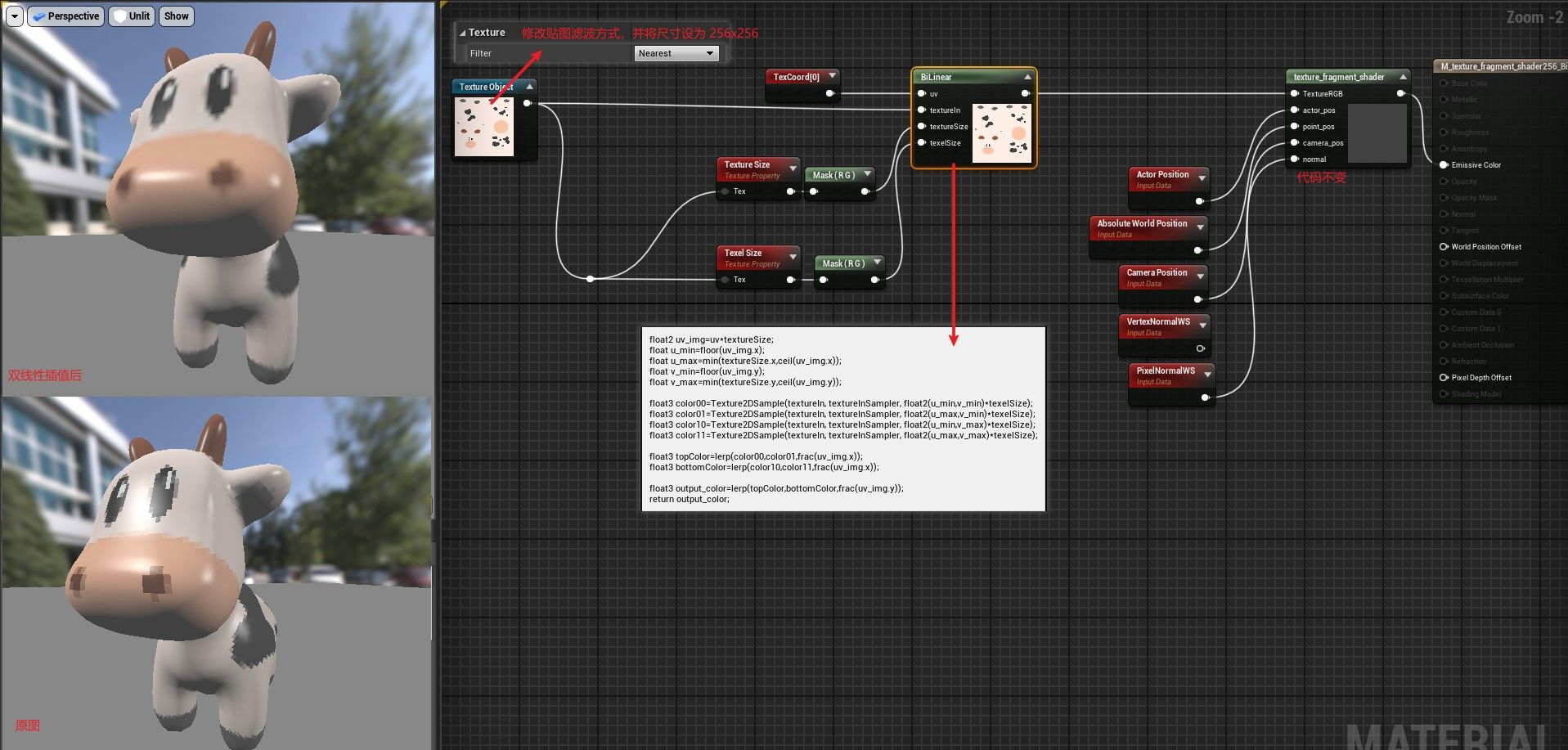
• 将贴图分辨率降低到 256x256 便于观察和比较，并在 texture 设置中将 filter 方式改为 Neast

• 在texture_fragment_shader的上，对 texture 输入进行自定义双线性插值

• HLSL 代码

  

Blinn-phong模型 bump_fragment_shader

• 直接代入公式，注意 y 和 z 的对换

• dU = kh * kn * (h(u+1/w,v)-h(u,v)) 中，h 代表范数（模长）

• HLSL 代码

  

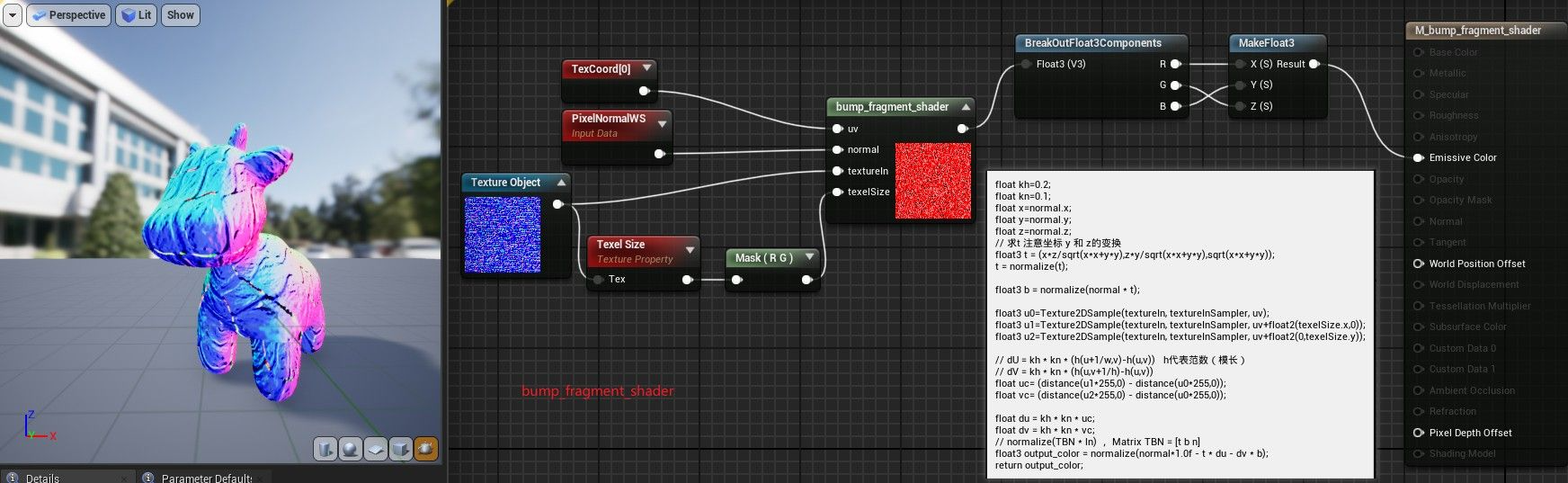
Blinn-phong模型 displacement_fragment_shader

• 将 bump_fragment_shader 中得到的法向量和位置作为光照计算公式的法向量和位置。

• HLSL 代码

  

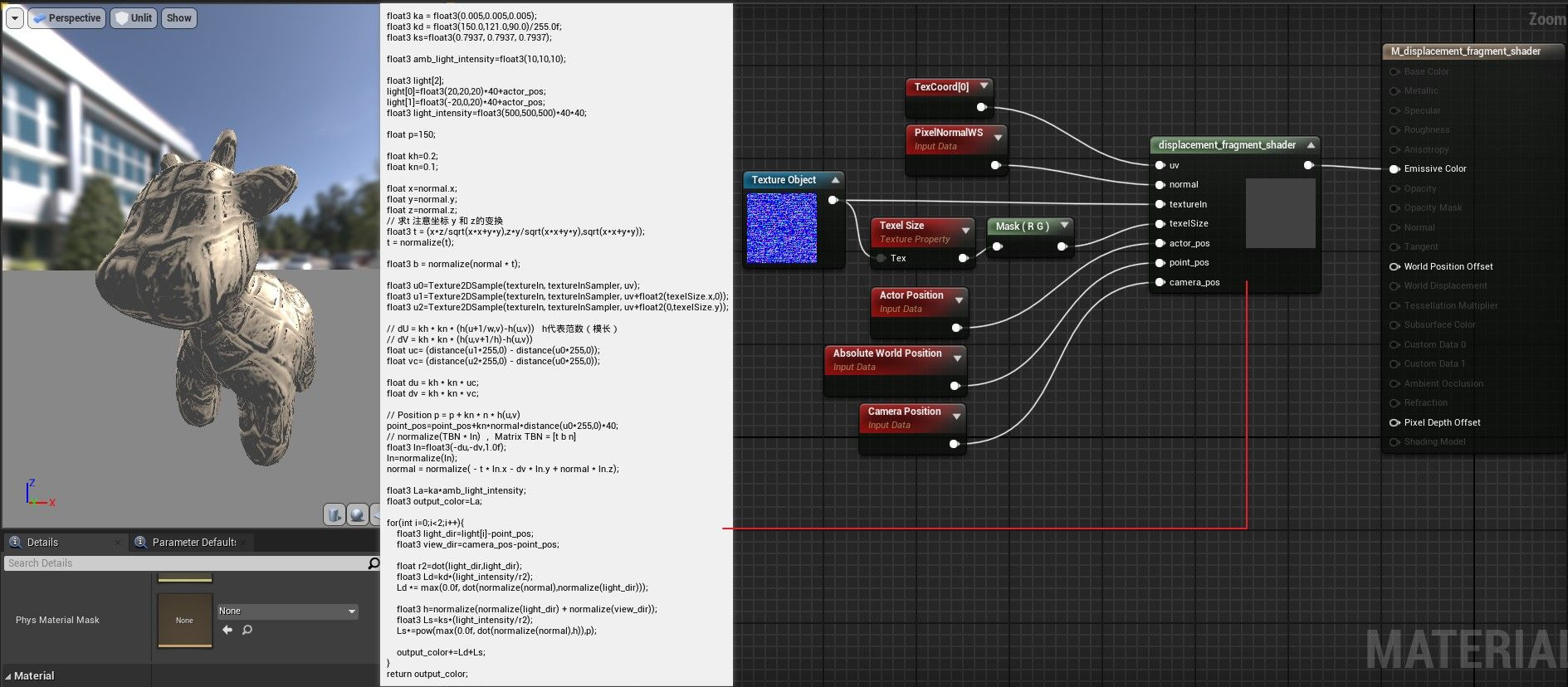
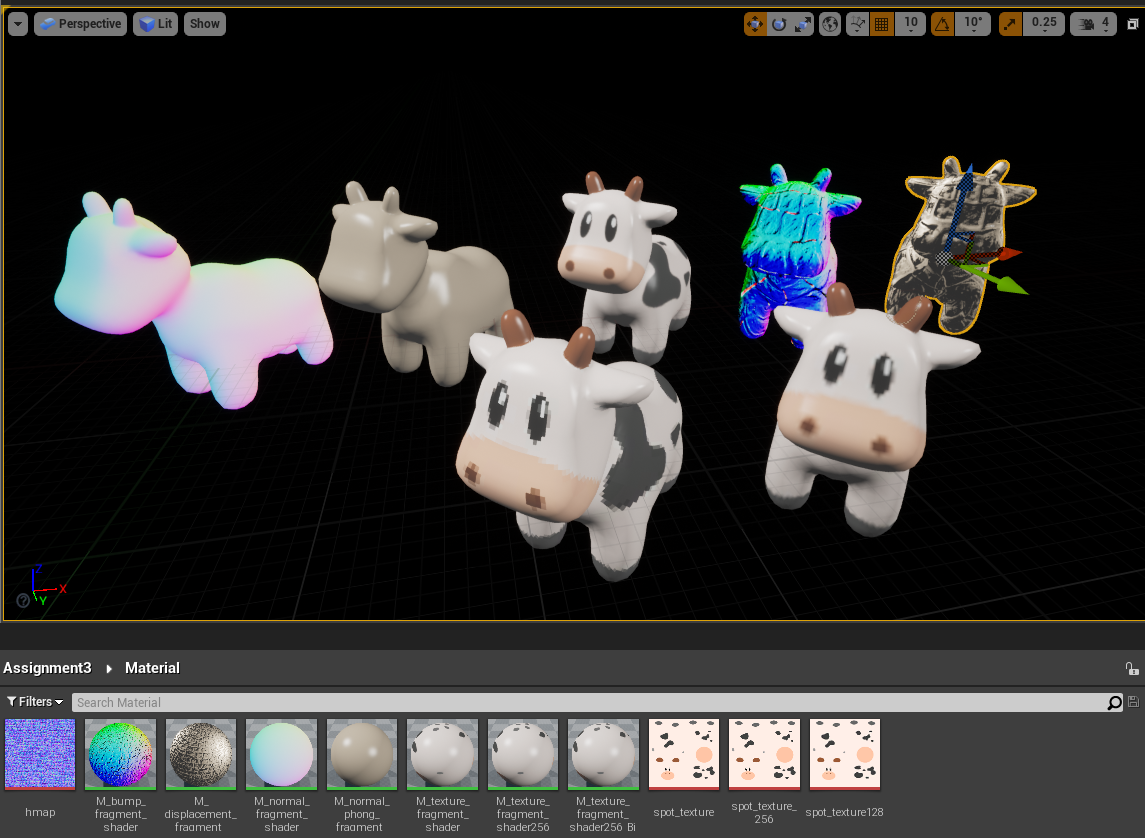
全家福