数据结构☞二叉搜索树BST

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它可以是一棵空树，也可以是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作

树的定义

树由一组以边连接的节点组成。公司的组织结构图就是一个树的例子，参见下图

组织结构图是用来描述一个组织的架构。在图 10-1 中，每个方框都是一个节点，连接方框

的线叫做边。节点代表了该组织中的各个职位，边描述了各职位间的关系。比如，CIO 直

接汇报给 CEO，那么两者就用一条边连接起来。开发经理向 CIO 汇报，也用一条边连接

起来。销售副总监和开发经理没有直接的联系，因此两个节点间没有用一条边相连。

下图的树展示了更多有关树的术语，在后续讨论中将会提到。一棵树最上面的节点称为

根节点，如果一个节点下面连接多个节点，那么该节点称为父节点，它下面的节点称为子

节点。一个节点可以有 0 个、1 个或多个子节点。没有任何子节点的节点称为叶子节点。

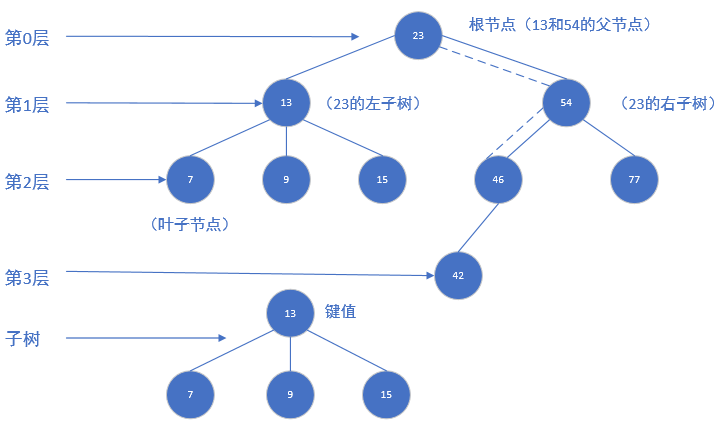
沿着一组特定的边，可以从一个节点走到另外一个与它不直接相连的节点。从一个节点到另一个节点的这一组边称为路径，在图中用虚线表示。以某种特定顺序访问树中所有的节点称为树的遍历。

树可以分为几个层次，根节点是第 0 层，它的子节点是第 1 层，子节点的子节点是第2层，以此类推。树中任何一层的节点可以都看做是子树的根，该子树包含根节点的子节点，子节点的子节点等。我们定义树的层数就是树的深度。

这种自上而下的树与人们的直觉相反。现实世界里，树的根是在底下的。在计算机科学里，自上而下的树则是个由来已久的习惯。事实上，计算机科学家高德纳曾经试图改变这个习惯，但没几个月他就发现，大多数计算机科学家都不愿用自然的、自下而上的方式描述树，于是，这件事也就只好不了了之。最后，每个节点都有一个与之相关的值，该值有时被称为键。

二叉树和二叉查找树

叉排序树的查找过程和次优二叉树类似，通常采取二叉链表作为二叉排序树的存储结构。中序遍历二叉排序树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉排序树变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。搜索,插入,删除的复杂度等于树高，O(log(n))

二叉树每个节点的子节点不允许超过两个。通过将子节点的个数限定为 2，可以写出高效的程序在树中插入、查找和删除数据。

下图展示了一棵二叉树

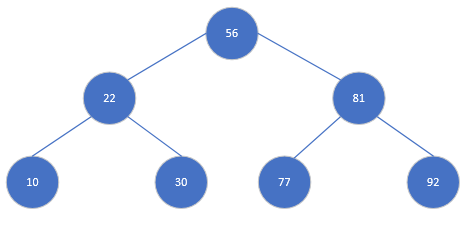
当考虑某种特殊的二叉树，比如二叉查找树时，确定子节点非常重要。二叉查找树是一种特殊的二叉树，相对较小的值保存在左节点中，较大的值保存在右节点中。这一特性使得查找的效率很高，对于数值型和非数值型的数据，比如单词和字符串，都是如此。

实现二叉查找树

实现Node

二叉查找树由节点组成，所以我们要定义的第一个对象就是 Node，该对象和链表类似。Node 类的定义如下：

class Node {
  constructor(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
}

Node 对象既保存数据，也保存和其他节点的链接（left 和 right）。

实现BST

现在可以创建一个类，用来表示二叉查找树（BST）。我们让类只包含一个数据成员：一个表示二叉查找树根节点的 Node 对象。该类的构造函数将根节点初始化为 null，以此创建一个空节点。BST 先要有一个 insert() 方法，用来向树中加入新节点。这个方法有点复杂，需要着重讲解。首先要创建一个 Node 对象，将数据传入该对象保存。

其次检查 BST 是否有根节点，如果没有，那么这是棵新树，该节点就是根节点，这个方法到此也就完成了；否则，进入下一步。

如果待插入节点不是根节点，那么就需要准备遍历 BST，找到插入的适当位置。该过程类似于遍历链表。用一个变量存储当前节点，一层层地遍历 BST。

进入 BST 以后，下一步就要决定将节点放在哪个地方。找到正确的插入点时，会跳出循环。查找正确插入点的算法如下。

1. 设根节点为当前节点。
2. 如果待插入节点保存的数据小于当前节点，则设新的当前节点为原节点的左节点；反
3. 之，执行第 4 步。
4. 如果当前节点的左节点为 null，就将新的节点插入这个位置，退出循环；反之，继续
5. 执行下一次循环。
6. 设新的当前节点为原节点的右节点。
7. 如果当前节点的右节点为 null，就将新的节点插入这个位置，退出循环；反之，继续
8. 执行下一次循环。
   
   有了上面的算法，就可以开始实现 BST 类了。

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
  insert(key) {
    // 插入
    const newNode = new Node(key);
    if (this.root === null) {
      this.root = newNode;
    } else {
      this.insertNode(this.root, newNode);
    }
  }
  insertNode(node, newNode) {
    if (newNode.key < node.key) {
      if (node.left === null) {
        node.left = newNode;
      } else {
        this.insertNode(node.left, newNode);
      }
    } else {
      if (node.right === null) {
        node.right = newNode;
      } else {
        this.insertNode(node.right, newNode);
      }
    }
  }
}

有三种遍历 BST 的方式：中序、先序和后序。中序遍历按照节点上的键值，以升序访问BST 上的所有节点。先序遍历先访问根节点，然后以同样方式访问左子树和右子树。后序遍历先访问叶子节点，从左子树到右子树，再到根节点

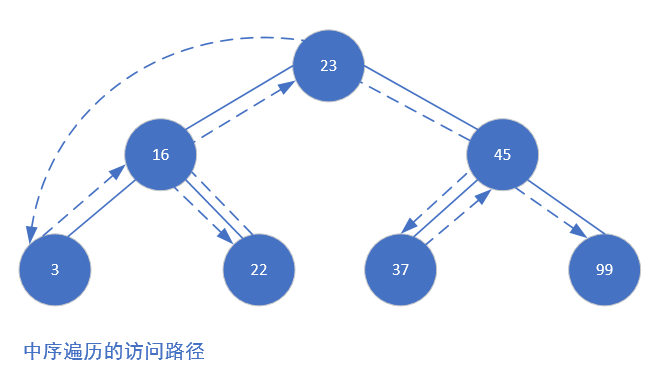
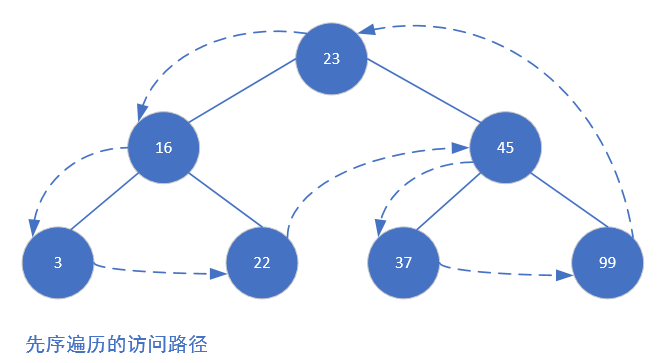
增加中序、先序和后序遍历

class BinarySearchTree {
  ...
  inOrderTraverse(callback) {
    // 中序查找
    this.inOrderTraverseNode(this.root, callback);
  }
  preOrderTraverse(callback) {
    // 先序查找
    this.preOrderTraverseNode(this.root, callback);
  }
  postOrderTraverse(callback) {
    // 后序查找
    this.postOrderTraverseNode(this.root, callback);
  }
  inOrderTraverseNode(node, callback) {
    if (node !== null) {
      this.inOrderTraverseNode(node.left, callback);
      callback(node.key);
      this.inOrderTraverseNode(node.right, callback);
    }
  }
  preOrderTraverseNode(node, callback) {
    if (node !== null) {
      callback(node.key);
      this.preOrderTraverseNode(node.left, callback);
      this.preOrderTraverseNode(node.right, callback);
    }
  }
  postOrderTraverseNode(node, callback) {
    if (node !== null) {
      this.postOrderTraverseNode(node.left, callback);
      this.postOrderTraverseNode(node.right, callback);
      callback(node.key);
    }
  }
}

在二叉查找树上进行查找

对 BST 通常有下列三种类型的查找：

1. 查找给定值；
2. 查找最小值；
3. 查找最大值。

class BinarySearchTree {
  ...
  min() {
    // 最小值
    return this.minNode(this.root);
  }
  max() {
    // 最大值
    return this.maxNode(this.root);
  }
  search(key) {
    // 查找
    this.searchNode(this.root, key);
  }
  minNode(node) {
    if (node) {
      while (node && node.left !== null) {
        node = node.left;
      }
      return node.key;
    }
    return null;
  }
  maxNode(node) {
    if (node) {
      while (node && node.right !== null) {
        node = node.right;
      }
      return node.key;
    }
    return null;
  }
  searchNode(node, key) {
    if (node === null) return false;
    if (key < node.key) {
      return this.searchNode(node.left, key);
    } else if (key > node.key) {
      return this.searchNode(node.right, key);
    } else {
      return true;
    }
  }
  findMinNode(node) {
    if (node) {
      while (node && node.left !== null) {
        node = node.left;
      }
      return node.key;
    }
    return null;
  }
}

从二叉查找树上删除节点

class BinarySearchTree {
  ...
  remove(key) {
    //移除树节点
    this.removeNode(this.root, key);
  }
  removeNode(node, key) {
    if (node === null) return null;

    if (key < node.key) {
      node.left = this.removeNode(node.left, key);
      return node;
    } else if (key > node.key) {
      node.right = this.removeNode(node.right, key);
      return node;
    } else {
      if (node.left === null && node.right === null) {
        node = null;
        return node;
      } else if (node.left === null) {
        node = node.right;
        return node;
      } else if (node.right === null) {
        node = node.left;
        return node;
      }

      const aux = this.findMinNode(node.right);
      node.key = aux.key;
      node.right = this.removeNode(node.right, aux.key);
      return node;
    }
  }
}

完整代码

class Node {
  constructor(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
  insert(key) {
    // 插入
    const newNode = new Node(key);
    if (this.root === null) {
      this.root = newNode;
    } else {
      this.insertNode(this.root, newNode);
    }
    console.log(this.root);
  }
  inOrderTraverse(callback) {
    // 中序查找
    this.inOrderTraverseNode(this.root, callback);
  }
  preOrderTraverse(callback) {
    // 先序查找
    this.preOrderTraverseNode(this.root, callback);
  }
  postOrderTraverse(callback) {
    // 后序查找
    this.postOrderTraverseNode(this.root, callback);
  }
  min() {
    // 最小值
    return this.minNode(this.root);
  }
  max() {
    // 最大值
    return this.maxNode(this.root);
  }
  search(key) {
    // 查找
    this.searchNode(this.root, key);
  }
  remove(key) {
    //移除树节点
    this.removeNode(this.root, key);
  }
  insertNode(node, newNode) {
    if (newNode.key < node.key) {
      if (node.left === null) {
        node.left = newNode;
      } else {
        this.insertNode(node.left, newNode);
      }
    } else {
      if (node.right === null) {
        node.right = newNode;
      } else {
        this.insertNode(node.right, newNode);
      }
    }
  }
  inOrderTraverseNode(node, callback) {
    if (node !== null) {
      this.inOrderTraverseNode(node.left, callback);
      callback(node.key);
      this.inOrderTraverseNode(node.right, callback);
    }
  }
  preOrderTraverseNode(node, callback) {
    if (node !== null) {
      callback(node.key);
      this.preOrderTraverseNode(node.left, callback);
      this.preOrderTraverseNode(node.right, callback);
    }
  }
  postOrderTraverseNode(node, callback) {
    if (node !== null) {
      this.postOrderTraverseNode(node.left, callback);
      this.postOrderTraverseNode(node.right, callback);
      callback(node.key);
    }
  }
  minNode(node) {
    if (node) {
      while (node && node.left !== null) {
        node = node.left;
      }
      return node.key;
    }
    return null;
  }
  maxNode(node) {
    if (node) {
      while (node && node.right !== null) {
        node = node.right;
      }
      return node.key;
    }
    return null;
  }
  searchNode(node, key) {
    if (node === null) return false;
    if (key < node.key) {
      return this.searchNode(node.left, key);
    } else if (key > node.key) {
      return this.searchNode(node.right, key);
    } else {
      return true;
    }
  }
  removeNode(node, key) {
    if (node === null) return null;

    if (key < node.key) {
      node.left = this.removeNode(node.left, key);
      return node;
    } else if (key > node.key) {
      node.right = this.removeNode(node.right, key);
      return node;
    } else {
      if (node.left === null && node.right === null) {
        node = null;
        return node;
      } else if (node.left === null) {
        node = node.right;
        return node;
      } else if (node.right === null) {
        node = node.left;
        return node;
      }

      const aux = this.findMinNode(node.right);
      node.key = aux.key;
      node.right = this.removeNode(node.right, aux.key);
      return node;
    }
  }
  findMinNode(node) {
    if (node) {
      while (node && node.left !== null) {
        node = node.left;
      }
      return node.key;
    }
    return null;
  }
}

参考书籍

数据结构与算法JavaScript描述