l2-loss,l2正则化,l2范数,欧式距离
欧式距离:
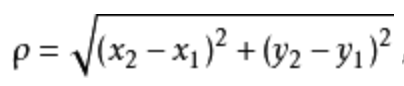
l2范数:
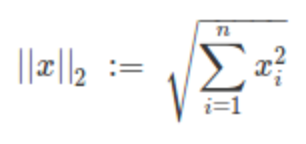
l2正则化:
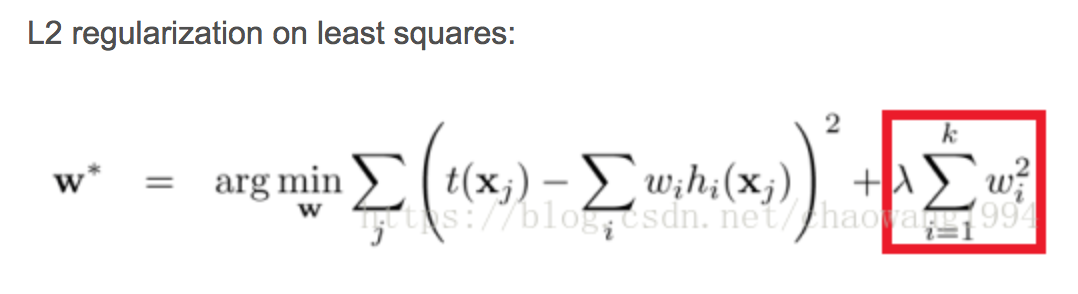
l2-loss(也叫平方损失函数):
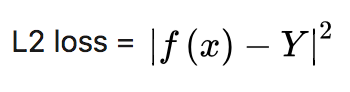
http://openaccess.thecvf.com/content_cvpr_2017/papers/Li_Mimicking_Very_Efficient_CVPR_2017_paper.pdf
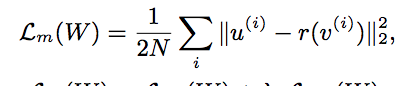
总结:l2范数和欧式距离很像,都是开根号。l2正则化和l2-loss都是直接开平方。上面这篇mimic的paper,就是用的l2-loss,可以看到他写的公式就是在l2范数上开平方。也可以这么理解,对于loss,需要求梯度,如果有根号后,梯度的计算就变得复杂了。
l2-loss,l2正则化,l2范数,欧式距离的更多相关文章
- L1 loss L2 loss
https://www.letslearnai.com/2018/03/10/what-are-l1-and-l2-loss-functions.html http://rishy.github.io ...
- [PCL]3 欧式距离分类EuclideanClusterExtraction
EuclideanClusterExtraction这个名字起的很奇怪,欧式距离聚类这个该如何理解?欧式距离只是一种距离测度的方法呀!有了一个Cluster在里面,我以为是某一种聚类算法,层次聚类?k ...
- 剑指Offer——网易笔试之不要二——欧式距离的典型应用
剑指Offer--网易笔试之不要二--欧式距离的典型应用 前言 欧几里得度量(euclidean metric)(也称欧氏距离)是一个通常采用的距离定义,指在m维空间中两个点之间的真实距离,或者向量的 ...
- 机器学习进阶-疲劳检测(眨眼检测) 1.dist.eculidean(计算两个点的欧式距离) 2.dlib.get_frontal_face_detector(脸部位置检测器) 3.dlib.shape_predictor(脸部特征位置检测器) 4.Orderdict(构造有序的字典)
1.dist.eculidean(A, B) # 求出A和B点的欧式距离 参数说明:A,B表示位置信息 2.dlib.get_frontal_face_detector()表示脸部位置检测器 3.dl ...
- L1与L2损失函数和正则化的区别
本文翻译自文章:Differences between L1 and L2 as Loss Function and Regularization,如有翻译不当之处,欢迎拍砖,谢谢~ 在机器学习实 ...
- L1 loss, L2 loss以及Smooth L1 Loss的对比
总结对比下\(L_1\) 损失函数,\(L_2\) 损失函数以及\(\text{Smooth} L_1\) 损失函数的优缺点. 均方误差MSE (\(L_2\) Loss) 均方误差(Mean Squ ...
- l1 l2 loss
衡量预测值与真实值的偏差程度的最常见的loss: 误差的L1范数和L2范数 因为L1范数在误差接近0的时候不平滑,所以比较少用到这个范数 L2范数的缺点是当存在离群点(outliers)的时候,这些点 ...
- 正则化--L2正则化
请查看以下泛化曲线,该曲线显示的是训练集和验证集相对于训练迭代次数的损失. 图 1 显示的是某个模型的训练损失逐渐减少,但验证损失最终增加.换言之,该泛化曲线显示该模型与训练集中的数据过拟合.根据奥卡 ...
- L2与L1正则化理解
https://www.zhihu.com/question/37096933/answer/70507353 https://blog.csdn.net/red_stone1/article/det ...
随机推荐
- Java学习--jsp内置对象
九个内置对象,其中Out,request,response,session,application常用 get与post区别: request对象: response对象: 请求转发与请求重定向的区别 ...
- 从MySQL到ORM(三):连接、存储过程和用户权限
一.联结表 数据仍使用前文中的数据. 1.子查询 作为子查询的SELECT语句只能查询单个列.企图检索多个列将返回错误. -- 作为查询条件使用 -- 查看TNT2订单对应的客户ip(order表) ...
- java 自定义 LRU(最近最少使用)策略 实现 缓存机制
1. java提供了一个简单的方式实现LRU: LinkedHashMap 2. 自定义实现 LRU至少需要两个主要操作: 添加(add)和搜索(search) public class LRU ...
- JAVASE(说出ArrayList,LinkedList的储存性能和特性)
说出ArrayList,和LinkedList的储存性能和特性? 答: ## ArrayList采用的是数组形式来保存对象的,这种方式将对象放在连续的位置中,优点是索引读取快,从最后插入和删除元素速 ...
- kindeditor之video插件开发
KindEditor是一套开源的HTML可视化编辑器,主要用于让用户在网站上获得所见即所得编辑效果.不仅结构小巧,而且功能强大,最主要的是它采用插件的开发管理方式,能很容易再它的基础上添加插件来实现自 ...
- Two references point to the same heap memory
Phone类 package com.itheima_03; /* * 手机类 */ public class Phone { String brand; int price; String colo ...
- 微信小程序开发11-HTTPS网络通信(重点)
1.OneNET平台支持https,将HTTP头部改成https://api.heclouds.com即可(重点!!!!!!!!) 2.如果我们需要从 https://test.com/getinfo ...
- HttpStatus
/* * Copyright 2002-2017 the original author or authors. * * Licensed under the Apache License, Vers ...
- MySQL案例05:CPU负载优化
最近有套系统数据库周末总是告警,CPU使用率超过90%,开始由开发那边再跟进处理,我也就没参与,后来发现没进展就登录上去看了下,然后进行了部分优化,优化后效果还是比较明显的,具体优化过程本文会做详细的 ...
- Linux操作NFS挂载、卸载等操作
一.NFS服务器的设置 NFS服务器的设定可以通过/etc/exports这个文件进行,设定格式如下 分享目录 主机名或IP(参数1,参数2) /binbin 172.17.1.*(rw,sync,n ...
