Angular 弹窗 控件

这个控件个人很喜欢，比起primgNG等弹窗组建，这款弹窗可以很轻松的定义自己的样式和布局。

可控参数有：宽度，高度，是否带有关闭图标，基本满足基础弹窗需求。

并且 Title/Content/Footer可以不强制三者并存。

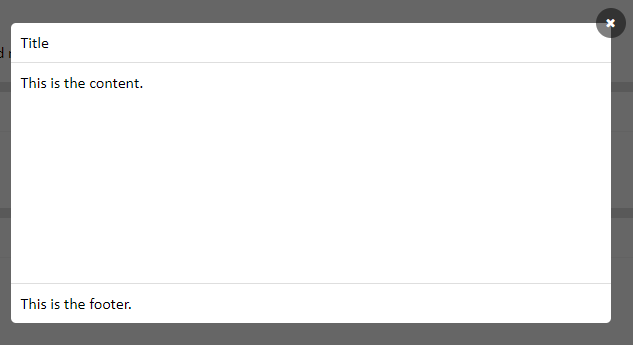
调用组件方法如下：

<popup-common *ngIf="showPupup" [width]="600" [height]="300" [closebtn]="true" (popupData)="closePopupFn($event)">
        <div class="popup-title">Title</div>
        <div class="popup-content">
            This is the content.
        </div>
        <div class="popup-footer">
            This is the footer.
        </div>
 </popup-common>

　

弹窗组件：

import { Component, OnInit, Input, Output, EventEmitter } from '@angular/core';

@Component ({
    selector: 'popup-common',
    template: `<div class="popup-mask">
                    <div class="popup-maskBox">
                        <div class="popup-maskContentBox" [ngStyle]="getStyle()">
                            <ng-content select=".popup-title"></ng-content>
                            <ng-content select=".popup-content"></ng-content>
                            <ng-content select=".popup-footer"></ng-content>
                            <span class="fa fa-close close-icon" *ngIf="closebtn" (click)="closePopupFn()"></span>
                        </div>
                    </div>
                </div>
                `,
    styles: [`
        .popup-maskContentBox {
            position: relative;
        }
        .close-icon {
            position: absolute;
            right: -15px;
            top: -15px;
            color: #fff;
            background: rgba(0,0,0,.5);
            border-radius: 50%;
            font-size: 12px;
            width: 30px;
            height: 30px;
            text-align: center;
            line-height: 30px;
        }
        .close-icon:hover {
            cursor: pointer;
        }
    `]
})

export class PopupCommonComponent implements OnInit {
    @Input() width: number;
    @Input() height: number;
    @Input() showPopup: boolean;
    @Input() closebtn: boolean = true;
    @Output() popupData = new EventEmitter();

    ngOnInit(){
        this.width = this.width != undefined ? this.width : 500;
    }

    getStyle(){
        return { width: this.width + 'px', height: this.height + 'px' }
    }

    closePopupFn(){
        this.showPopup = false;
        this.popupData.emit(this.showPopup);
    }

}