Solr相似度算法三：DRFSimilarity框架介绍

地址:http://terrier.org/docs/v3.5/dfr_description.html

The Divergence from Randomness (DFR) paradigm is a generalisation of one of the very first models of Information Retrieval, Harter's 2-Poisson indexing-model [1]. The 2-Poisson model is based on the hypothesis that the level of treatment of the informative words is witnessed by anelite set of documents, in which these words occur to a relatively greater extent than in the rest of the documents.

On the other hand, there are words, which do not possess elite documents, and thus their frequency follows a random distribution, which is the single Poisson model. Harter's model was first explored as a retrieval-model by Robertson, Van Rijsbergen and Porter [4]. Successively it was combined with standard probabilistic model by Robertson and Walker [3] and gave birth to the family of the BMs IR models (among them there is the well-known BM25 which is at the basis the Okapi system).

DFR models are obtained by instantiating the three components of the framework: selecting a basic randomness model, applying the first normalisation and normalising the term frequencies.

Basic Randomness Models

The DFR models are based on this simple idea: "The more the divergence of the within-document term-frequency from its frequency within the collection, the more the information carried by the word t in the document d". In other words the term-weight is inversely related to the probability of term-frequency within the document d obtained by a model M of randomness:

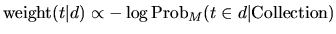(1)

where the subscript M stands for the type of model of randomness employed to compute the probability. In order to choose the appropriate model M of randomness, we can use different urn models. IR is thus seen as a probabilistic process, which uses random drawings from urn models, or equivalently random placement of coloured balls into urns. Instead of urns we have documents, and instead of different colours we have different terms, where each term occurs with some multiplicity in the urns as anyone of a number of related words or phrases which are called tokens of that term. There are many ways to choose M, each of these provides a basic DFR model. The basic models are derived in the following table.

Basic DFR Models
D	Divergence approximation of the binomial
P	Approximation of the binomial
B_E	Bose-Einstein distribution
G	Geometric approximation of the Bose-Einstein
I(n)	Inverse Document Frequency model
I(F)	Inverse Term Frequency model
I(n_e)	Inverse Expected Document Frequency model

If the model M is the binomial distribution, then the basic model is P and computes the value¹:

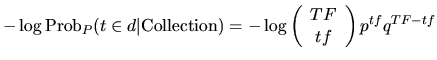(2)

where:

TF is the term-frequency of the term t in the Collection
tf is the term-frequency of the term t in the document d
N is the number of documents in the Collection
p is 1/N and q=1-p

Similarly, if the model M is the geometric distribution, then the basic model is G and computes the value:

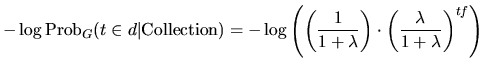(3)

where λ = F/N.

First Normalisation

When a rare term does not occur in a document then it has almost zero probability of being informative for the document. On the contrary, if a rare term has many occurrences in a document then it has a very high probability (almost the certainty) to be informative for the topic described by the document. Similarly to Ponte and Croft's [2] language model, we include a risk component in the DFR models. If the term-frequency in the document is high then the risk for the term of not being informative is minimal. In such a case Formula (1) gives a high value, but a minimal risk has also the negative effect of providing a small information gain. Therefore, instead of using the full weight provided by the Formula (1), we tune or smooth the weight of Formula (1) by considering only the portion of it which is the amount of information gained with the term:

(4)

The more the term occurs in the elite set, the less term-frequency is due to randomness, and thus the smaller the probability P_risk is, that is:

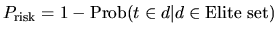(5)

We use two models for computing the information-gain with a term within a document: the Laplace L model and the ratio of two Bernoulli's processes B:

(6)

where df is the number of documents containing the term.

Term Frequency Normalisation

Before using Formula (4) the document-length dl is normalised to a standard length sl. Consequently, the term-frequencies tf are also recomputed with respect to the standard document-length, that is:

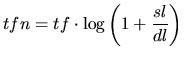(7)

A more flexible formula, referred to as Normalisation2, is given below:

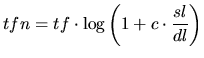(8)

DFR Models are finally obtained from the generating Formula (4), using a basic DFR model (such as Formulae (2) or (3)) in combination with a model of information-gain (such as Formula 6) and normalising the term-frequency (such as in Formula (7) or Formula (8)).

DFR Models in Terrier

Included with Terrier, are many of the DFR models, including:

Model	Description
BB2	Bernoulli-Einstein model with Bernoulli after-effect and normalisation 2.
IFB2	Inverse Term Frequency model with Bernoulli after-effect and normalisation 2.
In_expB2	Inverse Expected Document Frequency model with Bernoulli after-effect and normalisation 2. The logarithms are base 2. This model can be used for classic ad-hoc tasks.
In_expC2	Inverse Expected Document Frequency model with Bernoulli after-effect and normalisation 2. The logarithms are base e. This model can be used for classic ad-hoc tasks.
InL2	Inverse Document Frequency model with Laplace after-effect and normalisation 2. This model can be used for tasks that require early precision.
PL2	Poisson model with Laplace after-effect and normalisation 2. This model can be used for tasks that require early precision [7, 8]

Recommended settings for various collection are provided in Example TREC Experiments.

Another provided weighting model is a derivation of the BM25 formula from the Divergence From Randomness framework. Finally, Terrier also provides a generic DFR weighting model, which allows any DFR model to be generated and evaluated.

Query Expansion

The query expansion mechanism extracts the most informative terms from the top-returned documents as the expanded query terms. In this expansion process, terms in the top-returned documents are weighted using a particular DFR term weighting model. Currently, Terrier deploys the Bo1 (Bose-Einstein 1), Bo2 (Bose-Einstein 2) and KL (Kullback-Leibler) term weighting models. The DFR term weighting models follow a parameter-free approach in default.

An alternative approach is Rocchio's query expansion mechanism. A user can switch to the latter approach by settingparameter.free.expansion to false in the terrier.properties file. The default value of the parameter beta of Rocchio's approach is 0.4. To change this parameter, the user needs to specify the property rocchio_beta in the terrier.properties file.

Fields

DFR can encapsulate the importance of term occurrences occurring in different fields in a variety of different ways:

Per-field normalisation: The frequencies from the different fields in the documents are normalised with respect to the statistics of lengths typical for that field. This is as performed by the PL2F weighting model. Other per-field normalisation models can be generated using the generic PerFieldNormWeightingModel model.
Multinomial: The frequencies from the different fields are modelled in their divergence from the randomness expected by the term's occurrences in that field. The ML2 and MDL2 models implement this weighting.

Proximity

Proximity can be handled within DFR, by considering the number of occurrences of a pair of query terms within a window of pre-defined size. In particular, the DFRDependenceScoreModifier DSM implements the pBiL and pBiL2 models, which measure the randomness compared to the document's length, rather than the statistics of the pair in the corpus.

DFR Models and Cross-Entropy

A different interpretation of the gain-risk generating Formula (4) can be explained by the notion of cross-entropy. Shannon's mathematical theory of communication in the 1940s [5] established that the minimal average code word length is about the value of the entropy of the probabilities of the source words. This result is known under the name of the Noiseless Coding Theorem. The term noiseless refers at the assumption of the theorem that there is no possibility of errors in transmitting words. Nevertheless, it may happen that different sources about the same information are available. In general each source produces a different coding. In such cases, we can make a comparison of the two sources of evidence using the cross-entropy. The cross entropy is minimised when the two pairs of observations return the same probability density function, and in such a case cross-entropy coincides with the Shannon's entropy.

We possess two tests of randomness: the first test is P_risk and is relative to the term distribution within its elite set, while the second Prob_M is relative to the document with respect the entire collection. The first distribution can be treated as a new source of the term distribution, while the coding of the term with the term distribution within the collection can be considered as the primary source. The definition of the cross-entropy relation of these two probabilities distribution is:

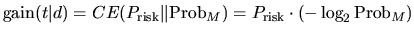(9)

Relation (9) is indeed Relation (4) of the DFR framework. DFR models can be equivalently defined as the divergence of two probabilities measuring the amount of randomness of two different sources of evidence.

For more details about the Divergence from Randomness framework, you may refer to the PhD thesis of Gianni Amati, or to Amati and Van Rijsbergen's paper Probabilistic models of information retrieval based on measuring divergence from randomness, TOIS 20(4):357-389, 2002.

[1] S.P. Harter. A probabilistic approach to automatic keyword indexing. PhD thesis, Graduate Library, The University of Chicago, Thesis No. T25146, 1974.
[2] J. Ponte and B. Croft. A Language Modeling Approach in Information Retrieval. In The 21st ACM SIGIR Conference on Research and Development in Information Retrieval (Melbourne, Australia, 1998), B. Croft, A.Moffat, and C.J. van Rijsbergen, Eds., pp.275-281.
[3] S.E. Robertson and S. Walker. Some simple approximations to the 2-Poisson Model for Probabilistic Weighted Retrieval. In Proceedings of the Seventeenth Annual International ACM-SIGIR Conference on Research and Development in Information Retrieval (Dublin, Ireland, June 1994), Springer-Verlag, pp. 232-241.
[4] S.E. Robertson, C.J. van Risjbergen and M. Porter. Probabilistic models of indexing and searching. In Information retrieval Research, S.E. Robertson, C.J. van Risjbergen and P. Williams, Eds. Butterworths, 1981, ch. 4, pp. 35-56.
[5] C. Shannon and W. Weaver. The Mathematical Theory of Communication. University of Illinois Press, Urbana, Illinois, 1949.
[6] B. He and I. Ounis. A study of parameter tuning for term frequency normalization, in Proceedings of the twelfth international conference on Information and knowledge management, New Orleans, LA, USA, 2003.
[7] B. He and I. Ounis. Term Frequency Normalisation Tuning for BM25 and DFR Model, in Proceedings of the 27th European Conference on Information Retrieval (ECIR'05), 2005.
[8] V. Plachouras and I. Ounis. Usefulness of Hyperlink Structure for Web Information Retrieval. In Proceedings of ACM SIGIR 2004.
[9] V. Plachouras, B. He and I. Ounis. University of Glasgow in TREC 2004: experiments in Web, Robust and Terabyte tracks with Terrier. In Proceedings of the 13th Text REtrieval Conference (TREC 2004), 2004.