初探动态规划（DP）

学习qzz的命名，来写一篇关于动态规划（dp）的入门博客。

动态规划应该算是一个入门oier的坑，动态规划的抽象即神奇之处，让很多萌新 萌比。

写这篇博客的目标，就是想要用一些容易理解的方式，讲解入门动态规划的真正意义。

奶萌兔的温馨提示：建议先理解dfs哦~(本文以一种较为新奇的方式解释DP)

动态规划

那什么是动态规划？

来问问神奇的奶萌兔吧（强行盗梗）！

（奶萌兔来给你讲解啦~虽然还在睡觉=w=）

动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题[]和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。
通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。
这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。----来自wiki百科

说这么多，DP能干什么？

奶萌兔的回答：解决一些问题...解决一些，dfs效率无法通过的问题。

不如先讲一道例题:

例1

　　爬楼梯：现在有n层楼梯，奶萌兔位于第0层 现在奶萌兔每一次可以往上爬1层或者2层，问奶萌兔爬到第n层有多少种方案？

这是一道经典的入门题，对于这道题，我们由简入深。

　　如何dfs？

　　这样考虑 dfs(int dep) 表示奶萌兔在第dep层。

　　那有两个走法，一个是dfs(dep+1) 一个是dfs(dep+2)。

　　而dfs的边界呢？ 则是 n 。 即 if (dep>n) return;

　　初始值？ dfs(0) 从第0层开始。

　　对于答案的统计？ 那就是每当dep为n时，说明到达了对ans统计加1。 即 if (dep==n) ans++ 且return;

　　说了怎么多dfs？对dp有个什么用啊！！！

　　这时候，奶萌兔来引入一个东西——状态。

　　状态是什么？用浅显易懂的解释就是，dfs需要保存的东西（不一定...），如dfs(int dep)  dep(奶萌兔当前的层数)就是一个状态。

　　而dp则是利用状态之间的相互关联，答案得以更新。

　　那下面，来讲 如何dp?

　　这样考虑 DP[dep] 表示奶萌兔从第0层走到第dep层时的方案数

　　依旧有两个走法，一个是DP[dep+1] 一个是DP[dep+2]。

　　是不是和dfs很相似？ 接下来是重点。

　　初始值 dp[0]=1 到第0层有一种方案，就是一开始就在0层。

　　DP[dep+1] DP[dep+2]会等于什么？

　　DP[dep+1]+=DP[dep] DP[dep+2]+=DP[dep]

　　因为走到第dep层的方案是DP[dep]，那么在走一层的时候，就只能走到dep+1的地方，那么dep上的全部方案，在通过走一步这样唯一的一个方法，可以到达dep+1，所以走到dep+1包含了dep上的方案，dep+2同理。

　　上面的两个式子就是状态转移方程了。

　　简单的转化一下， dp[dep+1]+=dp[dep] dp[dep+2]+=dep[dep] 则dp[dep]=dp[dep-1]+dp[dep-2] (当然不转化也是可以的，但对于部分题目，一些转化之后可能可以因此优化效率)

例2

　　从一个一维的题目，试试跳到二维。

　　骑士遍历：第一问可以直接往字典序最小去dfs，所以直接关注第二问吧

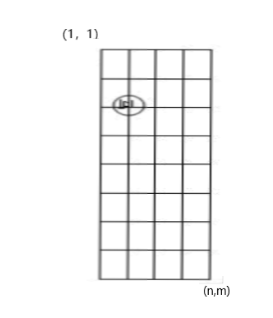
第二问：给一个n*m的棋盘，给定起点x1,y1 终点 x2,y2 在只能走日且只能向右走的情况下，问方案数。

这是例1的拓展，从一维的向上走，变为二维的向右走。

首先对于这样的棋盘，我们是不习惯的，因为与我们的数组顺序不同，让人烦心。

那怎么办捏?问问神奇的奶萌兔！

奶萌兔幽幽的说了一句：对~称~旋~转~

 哈！这是原来的题

哈！这还是原来的题

于是旋转一下之后，棋盘还是原来的棋盘，只是方向改变了。

题目就变成了只走日字且向下走的情况。

　　老规矩呢，如何dfs?

　　用用新名词，状态，dfs的状态是什么？ dfs(int x,int y) 表示当前奶萌兔骑士在(x,y)的位置。

　　那就是有四个走法

　　dfs(x+1,y+2)  dfs(x+2,y+1)   dfs(x+1,y-2) dfs(x+2,y-1)

　　边界 0 ，n    0 ，m 即 x>0且x<=n    y>0且y<=m

　　初始：dfs(x1,y1)

　　答案的统计:每当 x==x2&&y==y2 时说明到终点了，那ans++

　　dp类比就好啦，状态就是数组的下标。

　　DP[x][y] 表示奶萌兔骑士从(x1,y1)出发到(x,y) 的位置时的方案。

　　一样四个走法

　　DP[x+1][y+2] DP[x+2][y+1]  DP[x+1][y-2] DP[x+2][y-1]

　　边界是一样的哦~

　　初始：DP[x1][y1]=1 （在起点的时候就是一个方案）

　　答案：DP[x2][y2]

　　那转移方程，和例1一样哦，只是拓展为二维，走法变多一些。

　　DP[x+1][y+2]+=DP[x][y]     DP[x+2][y+1]+=DP[x][y]    DP[x+1][y-2]+=DP[x][y]     DP[x+2][y-1]+=DP[x][y]

　　简单转化一下： dp[x][y]=dp[x-1][y-2]+dp[x-2][y-1]+dp[x-1][y+2]+dp[x-2][y+1]；

　　好了问题来了:怎么转化的？ 不妨这样撕烤，固定住(x,y) 找找哪些点能到(x,y) 那些点的方案数加起来就是了（或者,对前面的方程变化，x+d改为x-d，y+d改为y-d  (d为常数)）。

 #define ll long long
 #include<cstdio>
 #include<iostream>
 using namespace std;
 ll f[][];
 int ansx[],ansy[];
 int n,m,x1,x2,y1,y2;
 const ll HR=1e18;
 void dfs(int dep,int nowx,int nowy){
     ansx[dep]=nowx;
     ansy[dep]=nowy;
     if (nowx==n&&nowy==m) {
         for (int i=;i<dep;i++)
             printf("(%d,%d)-",ansx[i],ansy[i]);
         printf("(%d,%d)",ansx[dep],ansy[dep]);
         exit();
     }
         //dfs的顺序注意按字典序最小。
     if (nowx+<=n&&nowy->) dfs(dep+,nowx+,nowy-);
     if (nowx+<=n&&nowy+<=m) dfs(dep+,nowx+,nowy+);
     if (nowx+<=n&&nowy->) dfs(dep+,nowx+,nowy-);
     if (nowx+<=n&&nowy+<=m) dfs(dep+,nowx+,nowy+);
 }
 int main(){
     scanf("%d%d%d%d%d%d",&n,&m,&x1,&y1,&x2,&y2);
     if (x1==) {
         dfs(,,); //第一问
         printf("NO");
         return ;
     }
         //第二问
     f[x1][y1]=;
     for (int i=x1+;i<=x2;i++){ //从x1+1开始，因为x1这一行是不可能更新的。
         for (int j=;j<=m;j++){
             if (j->) f[i][j]+=f[i-][j-]; //边界
             f[i][j]%=HR;
             f[i][j]+=f[i-][j+];
                         //为什么这个不判？原因是f[i-1][j+2]的值一定是0，因为无法更新到边界外的数，而初始值都是0，注意把数组开大即可，下面同理
             f[i][j]%=HR;
             f[i][j]+=f[i-][j-];
             f[i][j]%=HR;
             f[i][j]+=f[i-][j+];
             f[i][j]%=HR;
         }
     }
     printf("%lld",f[x2][y2]);
     return ;
 
 }        

例2

以上就是入门的方案数dp。

后期可能更新其他dp呀~