洛谷 P4139 上帝与集合的正确用法

题目描述

根据一些书上的记载，上帝的一次失败的创世经历是这样的：

第一天， 上帝创造了一个世界的基本元素，称做“元”。

第二天， 上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。

第三天， 上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。

第四天， 上帝创造了新的元素“γ”，“γ”被定义为“β”的集合。显然，一共会有16种不同的“γ”。

如果按照这样下去，上帝创造的第四种元素将会有65536种，第五种元素将会有2^65536种。这将会是一个天文数字。

然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素……

然而不久，当上帝创造出最后一种元素“θ”时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。

至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素“θ”一共有多少种？

上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对p取模后的值即可。

你可以认为上帝从“α”到“θ”一共创造了10^9次元素，或10^18次，或者干脆∞次。

一句话题意：

求$2^2^2^2^{...} mod p$

输入输出格式

输入格式：

第一行一个整数T，表示数据个数。

接下来T行，每行一个正整数p，代表你需要取模的值

输出格式：

T行，每行一个正整数，为答案对p取模后的值

输入输出样例

输入样例#1：

3
2
3
6

输出样例#1：

0
1
4

说明

对于100%的数据，T<=1000,p<=10^7

Solution：

本题罗嗦了很多，实际上就是求₂2^2∞ mod p的值。

我们直接想到使用扩展欧拉定理去降次：

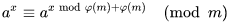， 其中 phi()为欧拉函数。

关于欧拉定理的一些知识见此  关于扩展欧拉定理的证明

那么本题我们直接递归调用该公式，phi(p)必定会一直变小，最后就是再套上快速幂的模板就行了。

代码：

#include <bits/stdc++.h>
#define il inline
#define ll long long
using  namespace  std;
il int gi()
{
    int a=;char x=getchar();bool f=;
    while((x<''||x>'')&&x!='-')x=getchar();
    if(x=='-')x=getchar(),f=;
    while(x>=''&&x<='')a=a*+x-,x=getchar();
    return f?-a:a;
}
il ll pow_mod(ll x, ll n, ll mod)
{
    ll res=;
    while(n>){
        if(n&)res=res*x%mod;
            x=x*x%mod;
            n>>=;
        }
     return res;
}
il int euler_phi(int n)
{
     int m=(int)sqrt(n+0.5);
     int ret=n;
     for(int i=;i<=m;++i)if(!(n%i))
        {
            ret=ret/i*(i-);
        while(!(n%i))n/=i;
        }
      if(n>)ret=ret/n*(n-);
      return ret;
}
il ll f(int x)
{
      if(x==)return ;
      int phi=euler_phi(x);
      return pow_mod(, f(phi)+phi, x);
}
int  main()
{
    int T,p;
      scanf("%d",&T);
    while(T--){scanf("%d",&p);  printf("%lld\n",f(p));}
    return ;
}