【bzoj5146】有趣的概率 微积分

题目描述

"可爱的妹子就像有理数一样多，但是我们知道的，你在数轴上随便取一个点取到有理数的概率总是0，"芽衣在床上自顾自的说着这句充满哲理的话，"诶，柚子，我写完概率论的作业你就和我出去约会怎么样""好呀，但是你要做完才可以哦"柚子回答道，芽衣立刻从床上翻下来冲到了座位上，诶，就一道题啊，真好，题目是这样的：在一个圆上任取n个点，求由这n个点依次围成的凸n边形至少有一个锐角的概率是多少，芽衣急于和柚子去约会，当然没有心情想这一道题，于是她就来求助聪明的你啦。

输入

一个n,4<=N<=10000000000

输出

至少有一个锐角的概率，为了避免精度问题，对1e9+7取模

样例输入

136865353

样例输出

423626558

---

题解

微积分

显然对于一张图，如果有锐角，则一定存在逆时针方向连续的两个角分别为钝角和锐角，且这样的连续两个角仅存在一组。

那么我们对这样的部分单独分析：

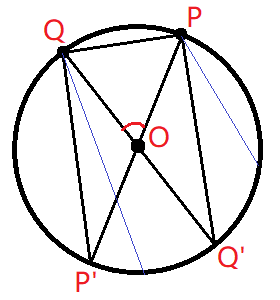
我们令点 $P$ 为该钝角，点 $Q$ 为该锐角。

那么在其余的点中，点 $P$ 逆时针前一个点一定在 $\widehat{PQ'}$ 上，点 $Q$ 逆时针后一个点一定在 $\widehat{PQ'P'}$ 上。

因此其余的点一定满足条件：全部在 $\widehat{PQ'P'}$ 上，且至少有一个在 $\widehat{PQ'}$ 上。

那么满足条件的概率就是：全部在 $\widehat{PQ'P'}$ 上的概率减去全部在 $\widehat{P'Q'}$ 上的概率。

设 $\angle POQ=x\times {2\pi}$ ，那么对于剩下 $n-2$ 个有标号点，都在 $\widehat{PQ'P'}$ 上的概率为 $(\frac 12)^{n-2}$ ，都在 $\widehat{P'Q'}$ 上的概率为 $x^{n-2}$ 。

因此对于固定的 $\angle POQ= x\times {2\pi}$ ，其余 $n-2$ 个点的选择满足条件的概率为 $(\frac 12)^{n-2}-x^{n-2}$ 。

所以对于无标号的 $P$ 和 $Q$ ，有标号的剩余点选择满足条件的概率就是 $\int_0^{\frac 12}((\frac 12)^{n-2}-x^{n-2})dx=\frac{n-2}{n-1}(\frac 12)^{n-1}$ 。

由于我们考虑的情况没有讨论到 $P$ 和 $Q$ 的标号，因此还要乘上 $P$ 和 $Q$ 的标号方案数 $n(n-1)$ 。

最终答案为 $n(n-2)(\frac 12)^{n-1}$ 。

时间复杂度 $O(\log n)$ 。

#include <cstdio>
#define mod 1000000007
int main()
{
    long long n , x = 500000004 , ans;
    scanf("%lld" , &n) , ans = n * (n - 2) % mod , n -- ;
    while(n)
    {
        if(n & 1) ans = ans * x % mod;
        x = x * x % mod , n >>= 1;
    }
    printf("%lld\n" , ans);
    return 0;
}