无向带权图的最小生成树算法——Prim及Kruskal算法思路

边赋以权值的图称为网或带权图，带权图的生成树也是带权的，生成树T各边的权值总和称为该树的权。

最小生成树（MST）：权值最小的生成树。

生成树和最小生成树的应用：要连通n个城市需要n－1条边线路。可以把边上的权值解释为线路的造价。则最小生成树表示使其造价最小的生成树。

构造网的最小生成树必须解决下面两个问题：

1、尽可能选取权值小的边，但不能构成回路；

2、选取n－1条恰当的边以连通n个顶点；

MST性质：假设G＝(V,E)是一个连通网，U是顶点V的一个非空子集。若(u,v)是一条具有最小权值的边，其中u∈U，v∈V－U，则必存在一棵包含边(u,v)的最小生成树。

1.prim算法

基本思想：假设G＝(V，E)是连通的，TE是G上最小生成树中边的集合。算法从U＝{u0}（u0∈V）、TE＝{}开始。重复执行下列操作：

在所有u∈U，v∈V－U的边(u，v)∈E中找一条权值最小的边(u0,v0)并入集合TE中，同时v0并入U，直到V＝U为止。

此时，TE中必有n-1条边，T=(V，TE)为G的最小生成树。

Prim算法的核心:始终保持TE中的边集构成一棵生成树。

注意：prim算法适合稠密图，其时间复杂度为O(n^2)，其时间复杂度与边得数目无关。

看了上面一大段文字是不是感觉有点晕啊，为了更好理解我在这里举一个例子，示例如下：

（1）图中有6个顶点v1-v6，每条边的边权值都在图上；在进行prim算法时，我先随意选择一个顶点作为起始点，当然我们一般选择v1作为起始点，好，现在我们设U集合为当前所找到最小生成树里面的顶点，TE集合为所找到的边，现在状态如下：

U={v1}； TE={}；

（2）现在查找一个顶点在U集合中，另一个顶点在V-U集合中的最小权值，如下图，在红线相交的线上找最小值。

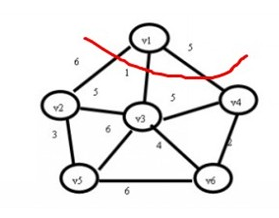
通过图中我们可以看到边v1-v3的权值最小为1，那么将v3加入到U集合，（v1，v3）加入到TE，状态如下：

U={v1，v3}； TE={（v1，v3）}；

（3）继续寻找，现在状态为U={v1，v3}； TE={（v1，v3）}；在与红线相交的边上查找最小值。

我们可以找到最小的权值为（v3，v6）=4，那么我们将v6加入到U集合，并将最小边加入到TE集合，那么加入后状态如下：

U={v1，v3，v6}； TE={（v1，v3），（v3，v6）}； 如此循环一下直到找到所有顶点为止。

（4）下图像我们展示了全部的查找过程：

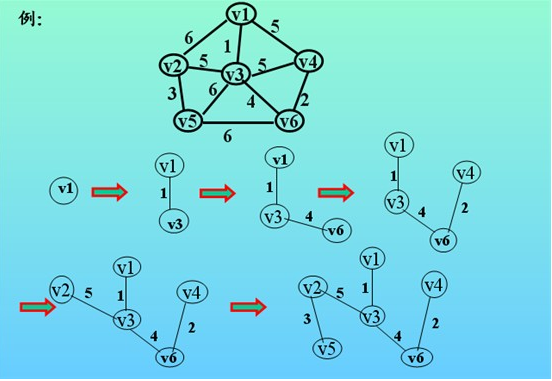
克鲁斯卡尔（Kruskal）算法（只与边相关）

算法描述：克鲁斯卡尔算法需要对图的边进行访问，所以克鲁斯卡尔算法的时间复杂度只和边又关系，可以证明其时间复杂度为O（eloge）。

算法过程：

1.将图各边按照权值进行排序

2.将图遍历一次，找出权值最小的边，（条件：此次找出的边不能和已加入最小生成树集合的边构成环），若符合条件，则加入最小生成树的集合中。不符合条件则继续遍历图，寻找下一个最小权值的边。

3.递归重复步骤1，直到找出n-1条边为止（设图有n个结点，则最小生成树的边数应为n-1条），算法结束。得到的就是此图的最小生成树。

克鲁斯卡尔（Kruskal）算法因为只与边相关，则适合求稀疏图的最小生成树。而prime算法因为只与顶点有关，所以适合求稠密图的最小生成树。

而kruskal算法的时间复杂度为O(eloge)跟边的数目有关，适合稀疏图。

算法描述：克鲁斯卡尔算法需要对图的边进行访问，所以克鲁斯卡尔算法的时间复杂度只和边又关系，可以证明其时间复杂度为O（ElogE）。

算法过程：

1.将图各边按照权值进行排序

2.将图遍历一次，找出权值最小的边，（条件：此次找出的边不能和已加入最小生成树集合的边构成环），若符合条件，则加入最小生成树的集合中。不符合条件则继续遍历图，寻找下一个最小权值的边。

3.递归重复步骤1，直到找出n-1条边为止（设图有n个结点，则最小生成树的边数应为n-1条），算法结束。得到的就是此图的最小生成树。判断是否构成环：《算法导论》提供的一种方法是采用一种"不相交集合数据结构"，也就是并查集了。核心内容就是如果某两个节点属于同一棵树，那么将它们合并后一定会形成回路。

克鲁斯卡尔（Kruskal）算法因为只与边相关，则适合求稀疏图的最小生成树。而prime算法因为只与顶点有关，所以适合求稠密图的最小生成树。