[BZOJ]|[Ural] Formula 1-----插头DP入门
1519. Formula 1
Memory limit: 64 MB
Background
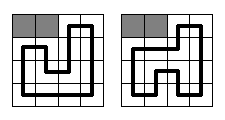
Problem
Input
Output
Samples
| input | output |
|---|---|
4 4 |
2 |
4 4 |
6 |
Problem Source: Timus Top Coders: Third Challenge
My submissions All submissions (10084) All accepted submissions (3166) Solutions rating (868)
题意:给出n*m的棋盘,有一些格子有障碍,求有多少个不经过障碍的哈密顿回路。

时合法的状态数总数为1333113个,可以解决本题。
4.可以发现轮廓线以上的路径一定互不相交,并且两两匹配,所以可以用括号序列来表示状态,0表示左括号"(",1表示右括号”)",括号的意义即使到轮廓线上的路径是出路径还是入路径。
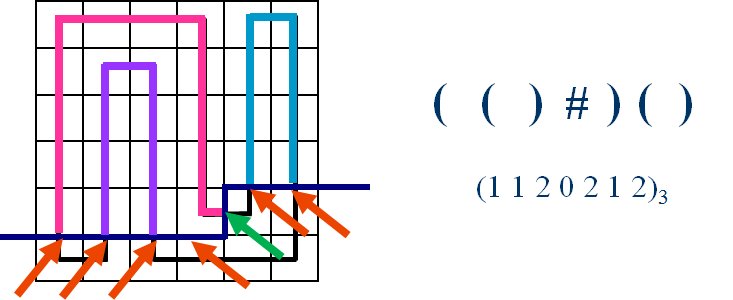
可以发现,一行有m个格子,但是却有m+1个状态,因为在转移的时候我们要考虑到,当前处理的格子的右边的情况(绿色箭头)
每一次转移之后相当于是轮廓线上当前决策格子的左插头改成下插头,上插头改成右插头的状态。
每一次转移之后改变的是对应格子轮廓线上连通的状态,我们只关心当前格子轮廓线以上的连线终止与轮廓线上(由于要形成哈密顿回路,所以不存在自环)的情况,而并不在意轮廓线之下的连线方式。
那么分情况考虑转移(把橘色的称为左插头,绿色的称为上插头)

(1)上,左插头都没有,而且当前格子(x,y),(x+1,y),(x,y+1)均不为障碍,则可以新建一个连通块。
...00... --------> ...12...
(2)仅有有上插头,或仅有下插头,延续原来的连通分量即可。
...10... --------> ...12...
(3)上下插头都有。
3.1,上下插头均为出路径,画图可知即使两个连通分量左边合并,需要找到相应状态最左边那个右括号将其修改为左括号。
.........2... -------> .........2
3.2,左插头为入路径,上插头为出路径,即直接将对应状态位置上的左右括号消去即可。
...12... ------> ...00...
3.3,做插头为出路径,右插头为入路径,这个情况下就是答案的状态了,而且只能出现在最右下角的那个格子(其余的不合法)。
细节
注意题目的空间,以及还可以加上的优化。
我们把每一次的状态hash起来(而不是动态存储)
一种数据 :
1
.
三进制存储?为了方便,我们采用4进制(位运算中两位来表示一位)
CODE:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#include<cstdlib>
#include<cmath>
#include<cstring>
using namespace std;
#define yyj(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
#define CC(a,b) memset(a,b,sizeof(a));
#define u64 unsigned long long
#define llg long long
const int sz=;
llg n,m,state[][sz],tail,hash[sz],bit[],tot[],nn,mm,k=;
u64 dp[][sz],ans; char mp[][]; llg init()
{
llg cs=;
CC(mp,);
CC(dp,);
tot[]=dp[][]=;
state[][]=;
ans=k=; char ch;
for (llg i=;i<=n;i++)
{
scanf("%c",&ch);
for (llg j=;j<=m;j++)
{
scanf("%c",&ch);
mp[i][j]=ch=='.';
if (ch=='.') cs++;
if (mp[i][j]) nn=i,mm=j;
}
}
return cs;
} void in(llg s,u64 sum)
{
llg p=s%sz;
while (hash[p])
{
if (state[k][hash[p]]==s)
{
dp[k][hash[p]]+=sum;
return ;
}
p++;
if (p==sz) p=;
}
hash[p]=++tot[k];
state[k][hash[p]]=s;
dp[k][hash[p]]=sum;
} void work()
{
for (llg i=;i<=n;i++)
{
for (llg j=;j<=m;j++)
{
k^=;
CC(hash,);
tot[k]=;
for (llg u=;u<=tot[-k];u++)
{
llg s=state[-k][u],p=(s>>bit[j-])&,q=(s>>bit[j])&;
u64 sum=dp[-k][u];
if (!mp[i][j])
{
if (!q && !p) in(s,sum);
}
else
{
if (!p && !q)
{
if (!mp[i][j+] || !mp[i+][j]) continue;
s=s^(<<bit[j-])^(<<bit[j]<<);
in(s,sum);
}
else
if (!p && q)
{
if (mp[i][j+]) in(s,sum);
if (mp[i+][j]) s=s^q*(<<bit[j-])^q*(<<bit[j]),in(s,sum);
}
else
if (p && !q)
{
if (mp[i+][j]) in(s,sum);
if (mp[i][j+]) s=s^p*(<<bit[j-])^p*(<<bit[j]),in(s,sum);
}
else
if (p+q==)
{
llg nd=;
for (llg u=j+;j<=m;u++)
{
llg w=(s>>bit[u])&;
if (w==) nd++;
if (w==) nd--;
if (!nd) {s-=(<<bit[u]); break;}
}
s=s^(<<bit[j])^(<<bit[j-]),in(s,sum);
}
else
if (p+q==)
{
llg nd=;
for (llg u=j-;u>=;--u)
{
llg w=(s>>bit[u])&;
if (w==) nd++;
if (w==) nd--;
if (!nd) {s+=(<<bit[u]); break;}
}
s=s^(<<bit[j]<<)^(<<bit[j-]<<);
in(s,sum);
}
else
if (p== && q==)
{
if (i==nn && j==mm) ans+=sum;
}
else
if (p== && q==)
{
s=s^(<<bit[j-]<<)^(<<bit[j]);
in(s,sum);
} }
}
}
for (llg j=;j<=tot[k];j++) state[k][j]<<=;
}
cout<<ans<<endl;
} int main()
{
//yyj("a");
for (llg i=;i<=;i++) bit[i]=(i<<);
while (scanf("%lld%lld",&n,&m)!=EOF)
{
if (init()%) {cout<<""<<endl; continue;}
work();
}
return ;
}
参考:《基于连通性状态压缩的动态规划问题_Cdq》》--陈丹琦
博客:http://www.cnblogs.com/Tunix/p/4312203.html
[BZOJ]|[Ural] Formula 1-----插头DP入门的更多相关文章
- URAL Formula 1 ——插头DP
[题目分析] 一直听说这是插头DP入门题目. 难到爆炸. 写了2h,各种大常数,ural垫底. [代码] #include <cstdio> #include <cstring> ...
- [URAL1519] Formula 1 [插头dp入门]
题面: 传送门 思路: 插头dp基础教程 先理解一下题意:实际上就是要你求这个棋盘中的哈密顿回路个数,障碍不能走 看到这个数据范围,还有回路处理,就想到使用插头dp来做了 观察一下发现,这道题因为都是 ...
- bzoj 1814 Ural 1519 Formula 1 ——插头DP
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=1814 普通的插头 DP .但是调了很久.注意如果合并两个 1 的话,不是 “把向右第一个 2 ...
- 【BZOJ1814】Ural 1519 Formula 1 插头DP
[BZOJ1814]Ural 1519 Formula 1 题意:一个 m * n 的棋盘,有的格子存在障碍,求经过所有非障碍格子的哈密顿回路个数.(n,m<=12) 题解:插头DP板子题,刷板 ...
- bzoj1814 Ural 1519 Formula 1(插头dp模板题)
1814: Ural 1519 Formula 1 Time Limit: 1 Sec Memory Limit: 64 MBSubmit: 924 Solved: 351[Submit][Sta ...
- 【Ural】1519. Formula 1 插头DP
[题目]1519. Formula 1 [题意]给定n*m个方格图,有一些障碍格,求非障碍格的哈密顿回路数量.n,m<=12. [算法]插头DP [题解]<基于连通性状态压缩的动态规划问题 ...
- Ural 1519 Formula 1 插头DP
这是一道经典的插头DP单回路模板题. 用最小表示法来记录连通性,由于二进制的速度,考虑使用8进制. 1.当同时存在左.上插头的时候,需要判断两插头所在连通块是否相同,若相同,只能在最后一个非障碍点相连 ...
- BZOJ.1210.[HNOI2004]邮递员(插头DP Hash 高精)
BZOJ 洛谷 http://www.cnblogs.com/LadyLex/p/7326874.html 插头DP.\(m+1\)个插头的状态需要用三进制表示:\(0\)表示无插头,\(1\)表示是 ...
- URAL1519 Formula 1 —— 插头DP
题目链接:https://vjudge.net/problem/URAL-1519 1519. Formula 1 Time limit: 1.0 secondMemory limit: 64 MB ...
随机推荐
- [py][mx]django邮箱注册的验证码部分-django-simple-captcha库使用
邮箱注册-验证码 验证码使用第三方库django-simple-captcha 这个安装图形插件步骤官网有哦 - 1.Install django-simple-captcha via pip: pi ...
- Gcc ------ gcc的使用简介与命令行参数说明
gcc的使用简介与命令行参数说明 2011年06月19日 20:29:00 阅读数:10221 2011-06-19 wcdj 参考:<GNU gcc嵌入式系统开发 作者:董文军> (一) ...
- HDU5012:Dice(bfs模板)
http://acm.hdu.edu.cn/showproblem.php?pid=5012 Problem Description There are 2 special dices on the ...
- webdriver鼠标上下滑动
有时候我们需要对窗口显示的页面上下滑动,以显示当前正在处理的位置,这就需要用到webdriver模拟鼠标上下滑动 package test20161201; import org.openqa.sel ...
- Fiddler过滤指定域名
Fiddler过滤指定域名的方法一 切换到fiddler右侧窗口的Filters选项卡,勾选顶部的“Use Filters”,找到Hosts区域,设置以下三个选项: 1.第一项有三个选项,不做更改: ...
- php中in_array使用注意
可能会导致长耗时: http://www.jb51.net/article/41446.htm
- kendo grid应用经验总结
学习网址 https://docs.telerik.com/kendo-ui/controls/editors/dropdownlist/overview https://demos.telerik. ...
- PKU2503_map应用
Description You have just moved from Waterloo to a big city. The people here speak an incomprehensib ...
- 《Kalchbrenner N, Grefenstette E, Blunsom P. A convolutional neural network for modelling sentences》
Kalchbrenner’s Paper Kal的这篇文章引用次数较高,他提出了一种名为DCNN(Dynamic Convolutional Neural Network)的网络模型,在上一篇(Kim ...
- BP神经网络的Java实现(转)
http://fantasticinblur.iteye.com/blog/1465497 课程作业要求实现一个BPNN.这次尝试使用Java实现了一个.现共享之.版权属于大家.关于BPNN的原理,就 ...
