hdu6390GuGuFishtion【数论】

GuGuFishtion

Time Limit: 3000/1500 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Total Submission(s): 1204    Accepted Submission(s): 459

Problem Description

Today XianYu is too busy with his homework, but the boring GuGu is still disturbing him!!!!!!

At the break time, an evil idea arises in XianYu's mind.

‘Come on, you xxxxxxx little guy.’

‘I will give you a function ϕ(x) which counts the positive integers up to x that are relatively prime to x.’

‘And now I give you a fishtion, which named GuGu Fishtion, in memory of a great guy named XianYu and a disturbing and pitiful guy GuGu who will be cooked without solving my problem in 5 hours.’

‘The given fishtion is defined as follow:

Gu(a,b)=ϕ(ab)ϕ(a)ϕ(b)

And now you, the xxxxxxx little guy, have to solve the problem below given m,n,p.’

(∑a=1m∑b=1nGu(a,b))(modp)

So SMART and KINDHEARTED you are, so could you please help GuGu to solve this problem?

‘GU GU!’ GuGu thanks.

Input

Input contains an integer T indicating the number of cases, followed by T lines. Each line contains three integers m,n,p as described above.

1≤T≤3

1≤m,n≤1,000,000

max(m,n)<p≤1,000,000,007

And given p is a prime.

Output

Please output exactly T lines and each line contains only one integer representing the answer.

Sample Input

1 5 7 23

Sample Output

2

Source

2018 Multi-University Training Contest 7

Recommend

chendu   |   We have carefully selected several similar problems for you:  6408 6407 6406 6405 6404

先去学习了一下欧拉函数

这道题根据欧拉函数的定义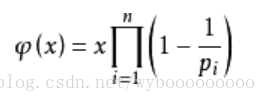化简可以得到

因此对于题目要求的

我们需要先计算每一个i/φ（i）的值， 再计算gcd（） = i的数对的数目

先预处理出所有的φi

对于一个数i,在a∈[1,n],b∈[1,m]a∈[1,n],b∈[1,m]的范围内,设f[i]为gcd为(i,2i,3i...)的对数设f[i]为gcd为(i,2i,3i...)的对数

显然 : f[i]=[n/i]∗[m/i]f[i]=[n/i]∗[m/i]

那么我们从大到小维护f[i]f[i],因为我们要的是 gcd=igcd=i 的对数,所以要把 gcd=2igcd=2i 的情况减去【预处理】

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<stack>
#define inf 1e18
using namespace std;

int t, n, m;
const int maxn = 1000005;
long long f[maxn], a[maxn], p;
long long cnt[maxn];

long long is[maxn], phi[maxn], pri[maxn], nump;
/*
特性 :
1.若a为质数,phi[a]=a-1;
2.若a为质数,b mod a=0,phi[a*b]=phi[b]*a
3.若a,b互质,phi[a*b]=phi[a]*phi[b](当a为质数时,if b mod a!=0 ,phi[a*b]=phi[a]*phi[b])
*/
void make()
{
    memset(phi, 0, sizeof(phi));
    memset(f, 0, sizeof(f));
    phi[1] = 1;
    for(int i = 2; i <= maxn; i++){
        if(!is[i]){//i是素数
            pri[++nump] = i;
            phi[i] = i - 1;
        }
        for(int j = 1; j <= nump && pri[j] * i < maxn; j++){//筛
            is[pri[j] * i] = 1;
            if(i % pri[j] == 0){
                phi[pri[j] * i] = phi[i] * pri[j];
                break;
            }
            else phi[pri[j] * i] = phi[i] *(pri[j] - 1);
        }
    }

    cnt[1] = 1;
    for(int i = 1; i < maxn; i++){
        for(int j = 2 * i; j < maxn; j += i){
            cnt[j] -= cnt[i];
        }
    }
}

void deal()
{
    f[1] = 1;
    for(int i = 2; i <= min(n, m); i++)
        f[i] = f[p % i] * (p - p / i) % p;
    for(int i = 1; i <= min(n, m); i++){
        a[i] = (long long)i * f[phi[i]] % p;
    }
}

long long get(int n, int m)
{
    long long ans = 0;
    for(int i = 1; i <= min(n, m); i++){
        ans+= (long long ) cnt[i] * (n / i) * (m / i);
        ans %= p;
    }
    return ans;
}

int main()
{
    make();
    cin>>t;
    while(t--){
        scanf("%d%d%lld", &m, &n, &p);
        deal();
        long long ans = 0;
        for(int i = 1; i <= min(n, m); i++){
            ans += (long long )a[i] * get(n / i, m / i);
            ans %= p;
        }
        printf("%lld\n", ans);
    }
    return 0;
}