nyoj 吃土豆

吃土豆

时间限制：1000 ms  |  内存限制：65535 KB

难度：4

 

描述

Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.

Now, how much qualities can you eat and then get ?

 

输入

There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that the quality of bean isn't beyond 1000, and 1<=M,N<=500.

输出

For each case, you just output the MAX qualities you can eat and then get.

样例输入

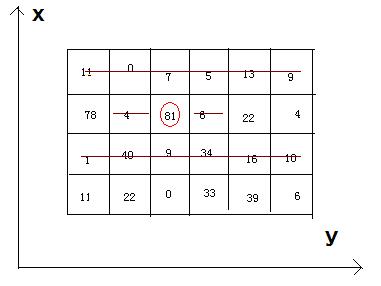
4 6
11 0 7 5 13 9
78 4 81 6 22 4
1 40 9 34 16 10
11 22 0 33 39 6

样例输出

242

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cmath>
using namespace std;

int a[505][505];

int main()
{
int m,n;
while(cin>>m>>n)
{
memset(a,0,sizeof(a));
freopen("1.txt","r",stdin);
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
cin>>a[i][j];
int Max;
for(int i=0;i<m;i++)
{
Max=a[i][n-1];
for(int j=n-1;j>=0;j--)
{
a[i][j]+=max(a[i][j+2],a[i][j+3]);
Max=max(Max,a[i][j]);
}
a[i][0]=Max;
}

Max=a[0][0];
a[2][0]+=a[0][0];
for(int i=3;i<m;i++)
{
a[i][0]+=max(a[i-2][0],a[i-3][0]);
Max=max(Max,a[i][0]);
}
cout<<Max<<endl;
}
return 0;
}

思路：

题目大意是如果某个土豆吃了，他的上下左右就不能吃了。

所以可以先对每行求最大。放在每行的行首，

再对第一列求最大。

数的不连续的和的最大值