【BZOJ5146】有趣的概率

Description

"可爱的妹子就像有理数一样多，但是我们知道的，你在数轴上随便取一个点取到有理数的概率总是0，"芽衣在床上自顾自的说着这句充满哲理的话，"诶，柚子，我写完概率论的作业你就和我出去约会怎么样""好呀，但是你要做完才可以哦"柚子回答道，芽衣立刻从床上翻下来冲到了座位上，诶，就一道题啊，真好，题目是这样的：在一个圆上任取n个点，求由这n个点依次围成的凸n边形至少有一个锐角的概率是多少，芽衣急于和柚子去约会，当然没有心情想这一道题，于是她就来求助聪明的你啦。

Input

一个n,4<=N<=10000000000

Output

至少有一个锐角的概率，为了避免精度问题，对1e9+7取模

Sample Input

136865353

Sample Output

423626558

题解：思路比较简单，过程比较复杂的数学题。首先本题有两种统计方法，一种的点是无标号的，另一种的点是有标号的，显然二者答案相等，但是无标号的比有标号的恶心多了。。。不过由于本人比较sb采用了无标号的方法，所以这里先讲我的做法：

至少有一个锐角等价于存在一个点，他左右两个点之间夹的圆弧大于一个半圆。所以我们不妨设圆是由$S$个点组成的（$S\rightarrow \infty$），那么我们先钦定一个角做锐角，再固定它左边的点不动，然后枚举剩下的那段圆弧的长度，便能得到某个角是锐角的概率：

$p_1={\sum\limits_{i=1}^{\frac S 2}(S-i)C_i^{n-3} \over C_S^{n-1}}$ ----(1)

运用一点组合知识，便能将这个式子化简到这个形式：$p_1={n\over 2^{n-1}}$。（如果你组合学得不好，本文最后会给出推导过程。）

有n个点，所以概率再乘上n，但是我们好像忽视了一个情况：圆内一个凸多边形可能有两个锐角！

所以我们把这个重复的部分去掉即可，由于两个锐角一定是相邻的，所以我们可以钦定某两个点是锐角，某对相邻的角全是锐角的概率是：

$p_2={\sum\limits_{i=1}^{\frac S 2}(\frac S 2-i)C_i^{n-2} \over C_S^{n-1}}$ ----(2)

推导过程类似，最后得到：$p_2=\frac 1 {2^{n-2}}$

所以最终答案就是：$(p_1-p_2)n=\frac {n(n-2)} {2^{n-1}}$。

如果用有标号的方法的话（Orz xqz），用微积分可以很快的解决问题（其实本质思想差不多），这里不给出式子了（其实是没学过）。

代码就不贴了。。。

附推导过程↓↓↓

先声明，在后面的式子中，某些变量趋近于无穷，因此我会舍弃它们后面的常数项。具体过程如下：

首先解释(1),(2)式的含义。(1)式中，我们先固定了一个点A，然后选择了A在顺时针方向的后两个点B,C，接着枚举了剩下那段圆弧的长度i，其中B对应的角是锐角，i可以看作弧AC的长度。那么，B的位置可以在剩余S-i个点中任取，其余n-3个点可以在i个点中任取，所以就是$(S-i)C_i^{n-3}$。最后总方案数可以看成固定一个点，其余的点在S中任取，就是$C_S^{n-1}$。

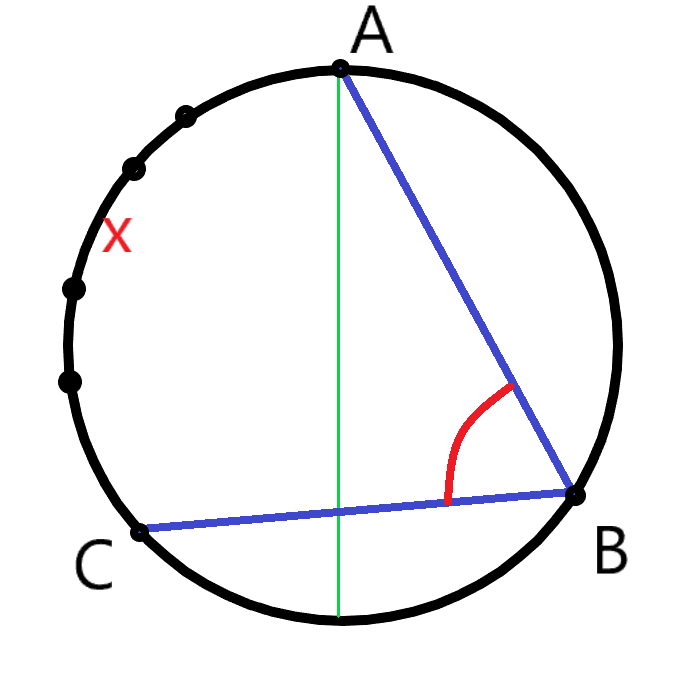
我们将分子的(S-i)拆开处理，然后将S提出来。首先有$\sum\limits_{i=1}^m C_i^n=C_m^{n+1}$，因为这可以看成在m个物品中选n个，你枚举编号最大的那个物品的编号得到的结果。于是前一部分就变成$S\times C_{S\over 2}^{n-2}$。又因为$iC_i^n=(i+1)C_i^n=(n+1)C_i^{n+1}$，所以我们又可以套用前面的式子，那么后一部分就变成了$(n-2)\times C_{S\over 2}^{n-1}$。

继续化简：${S\cdot C_{S\over 2}^{n-2}-(n-2)C_{S\over 2}^{n-1}\over C_S^{n-1}}\\={{2\cdot {S\over 2}({S\over 2})!\over (n-2)!({S\over 2}-(n-2))!}-{(n-2)({S\over 2})!\over (n-1)!({S\over 2}-(n-1))!}\over{S!\over (n-1)!(S-(n-1))!}}\\={{2(n-1)({S\over 2})!\over (n-1)!({S\over 2}-(n-1))!}-{(n-2)({S\over 2})!\over (n-1)!({S\over 2}-(n-1))!}\over{S!\over (n-1)!(S-(n-1))!}}\\={n({S\over 2}!)(S-(n-1))!\over S!({S\over 2}-(n-1))!}\\={n\over 2^{n-1}}$

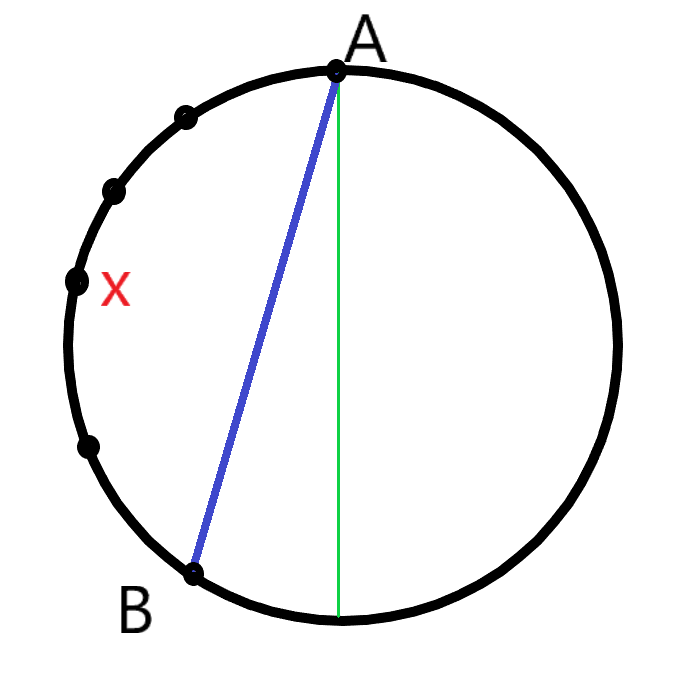
(2)式中，我们先固定了固定了一个点a，然后选择它在顺时针方向的下一个点b，要求a顺时针到b的这条圆弧大于一个半圆，接着枚举b到a这段劣弧的长度i，那么b可以在${S\over 2}-i$个点里选，剩余的点可以在i个点里选，这样就能保证角a和角b都是锐角了。方案数是$({S\over 2}-i)C_i^{n-2}$。推导过程略。