剑指Offer 35. 数组中的逆序对 （数组）

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

输入描述:

题目保证输入的数组中没有的相同的数字

数据范围：

对于%50的数据,size<=10^4

对于%75的数据,size<=10^5

对于%100的数据,size<=2*10^5

示例1

输入

复制

1,2,3,4,5,6,7,0

输出

复制

7

题目地址

https://www.nowcoder.com/practice/96bd6684e04a44eb80e6a68efc0ec6c5?tpId=13&tqId=11188&rp=2&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

思路

思路1：暴力解法，顺序扫描整个数组，每扫描到一个数字的时候，逐个比较该数字和它后面的数字的大小。如果后面的数字比它小，则这两个数字就组成一个逆序对。假设数组中含有n个数字，由于每个数字都要和O(n)个数字作比较，因此这个算法的时间复杂度是O(n^2)。

思路2：分治思想，采用归并排序的思路来处理，如下图，先分后治：

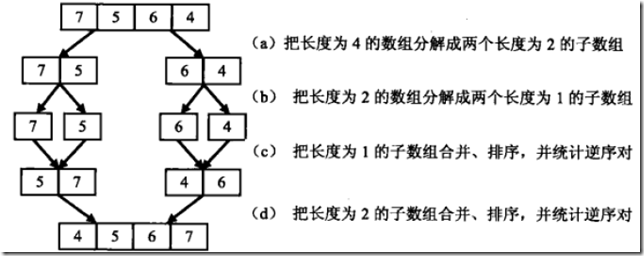
先把数组分解成两个长度为2的子数组，再把这两个子数组分解成两个长度为1的子数组。接下来一边合并相邻的子数组，一边统计逆序对的数目。在第一对长度为1的子数组{7}、{5}中7>5，因此（7,5）组成一个逆序对。同样在第二对长度为1的子数组{6}，{4}中也有逆序对（6,4），由于已经统计了这两对子数组内部的逆序对，因此需要把这两对子数组进行排序，避免在之后的统计过程中重复统计。

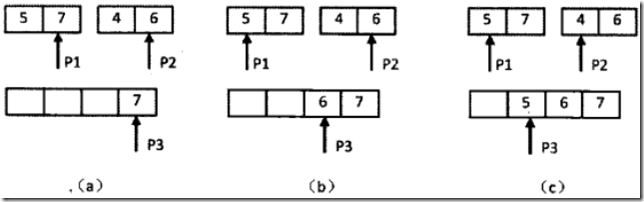
逆序对的总数 = 左边数组中的逆序对的数量 + 右边数组中逆序对的数量 + 左右结合成新的顺序数组时中出现的逆序对的数量

总结一下：

这是一个归并排序的合并过程，主要是考虑合并两个有序序列时，计算逆序对数。

对于两个升序序列，设置两个下标：两个有序序列的末尾。每次比较两个末尾值，如果前末尾大于后末尾值，则有”后序列当前长度“个逆序对；否则不构成逆序对。然后把较大值拷贝到辅助数组的末尾，即最终要将两个有序序列合并到辅助数组并有序。

这样，每次在合并前，先递归地处理左半段、右半段，则左、右半段有序，且左右半段的逆序对数可得到，再计算左右半段合并时逆序对的个数。

Python

# -*- coding:utf-8 -*-
class Solution:
    def InversePairs(self, data):
        # write code her
        if len(data)<=1:
            return 0
        # 思路1：运行超时
        # p = 0
        # for i in range(len(data)-1):
        #     for j in range(i+1,len(data)):
        #         if data[i] > data[j]:
        #             p += 1
        # return p % 1000000007
        # 思路2：归并排序
        temp = [x for x in data]
        return self.MSort(data,temp,0,len(data)-1)% 1000000007
    def MSort(self,data,temp,low,high):
        if low>=high:
            temp[low] = data[low]
            return 0
        mid = (low+high)//2
        left = self.MSort(temp,data,low,mid)
        right = self.MSort(temp,data,mid+1,high)
        count = 0
        i = low
        j = mid+1
        index = low
        while i <=mid and j <= high:
            if data[i]<=data[j]:
                temp[index] = data[i]
                i += 1
            else:
                temp[index] = data[j]
                j += 1
                count += mid-i+1
            index += 1
        while i <= mid:
            temp[index] = data[i]
            i += 1
            index += 1
        while j <= high:
            temp[index] = data[j]
            j += 1
            index += 1
        return count + left + right

if __name__ == '__main__':
    result = Solution().InversePairs([1,2,3,0])
    print(result)