LCA树上倍增

LCA就是最近公共祖先，比如

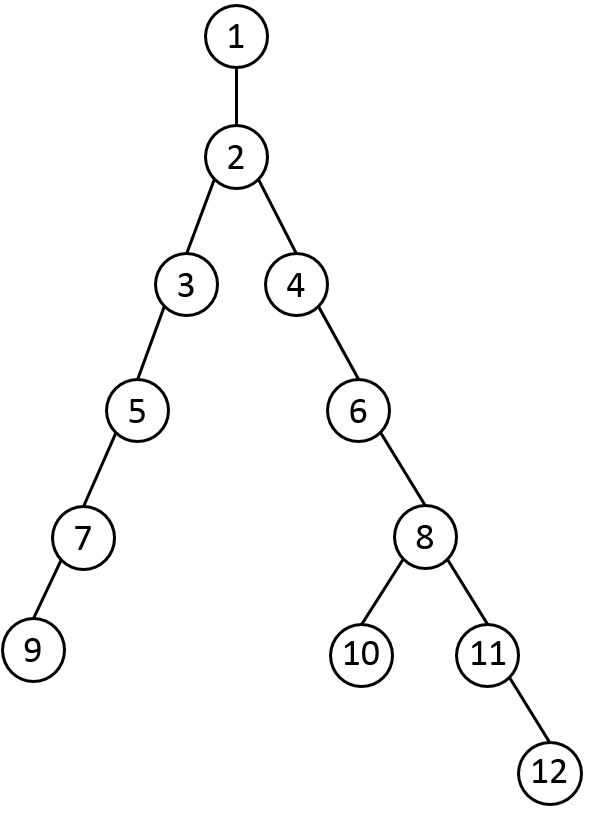
节点10和11的LCA就是8,9和3的LCA就是3。

我们这里讲一下用树上倍增来求LCA。

大家都可以写出暴力解法，两个节点依次一步一步往上爬，直到爬到了相同的一个节点。

二树上倍增就是对暴力的优化，改成了一次爬好几步。

具体怎么爬呢？就是两个点每次爬 2^j 步，而 j 满足的是两个点爬到的点不能相同，因为这样可能是公共祖先，但不一定是最近的。在这种条件下要使 j 尽可能的大。

举个例子，比如上图的节点7和8，当 j = 2 时，都爬到了节点 1，然而很显然这不是 LCA(7, 8)，所以只能取 j = 1,7和8分别跳到3和4。然后发现3和4跳不了了，算法结束，答案就是3和4的父亲节点2。

还有一个小点，若两个点深度不同，只需让深的点往上跳到相同的深度就行。

接下来就开始写代码了。

先要预处理节点 i 跳 2^j 步跳到的点是什么。开一个数组fa[i][j]，代表了节点i向上爬了2^j 步所到达的节点。那么递推式就是 fa[i][j] = fa[fa[i][j - 1]][j - 1]。

然后就直接可以求LCA了。

以洛谷的板子为例。传送门：https://www.luogu.org/problemnew/show/P3379

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<algorithm>
 #include<cstring>
 #include<vector>
 using namespace std;
 const int maxn = 5e5 + ;
 vector<int>v[maxn];
 int dep[maxn], fa[maxn][],vis[maxn];
 void dfs(int now)        //预处理
 {
     vis[now] = ;
     for(int i = ; ( << i) <= dep[now]; ++i)
         fa[now][i] = fa[fa[now][i - ]][i - ];
     for(int i = ; i < v[now].size(); ++i)
         if(!vis[v[now][i]])
         {
             dep[v[now][i]] = dep[now] + ;
             fa[v[now][i]][] = now;    //就是v[now][i]的父亲now
             dfs(v[now][i]);
         }
 }
 int lca(int x, int y)    //O(logn)
 {
     if(dep[x] < dep[y]) swap(x, y);
     for(int i = ; i >= ; --i)    //使x, y深度相同
         if(dep[x] - ( << i) >= dep[y]) x = fa[x][i];
     if(x == y) return x; //若两点正好重合，直接返回
     for(int i = ; i >= ; --i)
         if(fa[x][i] != fa[y][i])
         {
             x = fa[x][i]; y = fa[y][i];
         }
     return fa[x][];    //x的父亲节点就是x向上跳2^0步
 }
 int main()
 {
     int n, m, s; scanf("%d%d%d", &n, &m, &s);
     for(int i = ; i < n; ++i)
     {
         int a, b; scanf("%d%d", &a, &b);
         v[a].push_back(b); v[b].push_back(a);
     }
     dfs(s);
     while(m--)
     {
         int a, b; scanf("%d%d", &a, &b);
         printf("%d\n", lca(a, b));
     }
     return ;
 }

时间复杂度是O(nlogn)。