KD-树（下）

来自于https://zhuanlan.zhihu.com/p/23966698

构造 kd 树的例子

上面抽象的定义和算法确实是很不好理解，举一个例子会清楚很多。首先随机在 中随机生成 13 个点作为我们的数据集。起始的切分轴；这里 对应 xx 轴，而 对应 y 轴。

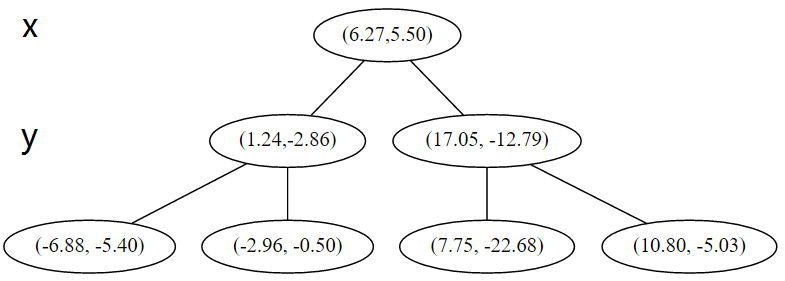
首先先沿 x 坐标进行切分，我们选出 x 坐标的中位点，获取最根部节点的坐标

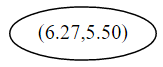并且按照该点的x坐标将空间进行切分，所有 x 坐标小于 6.27 的数据用于构建左枝，x坐标大于 6.27 的点用于构建右枝。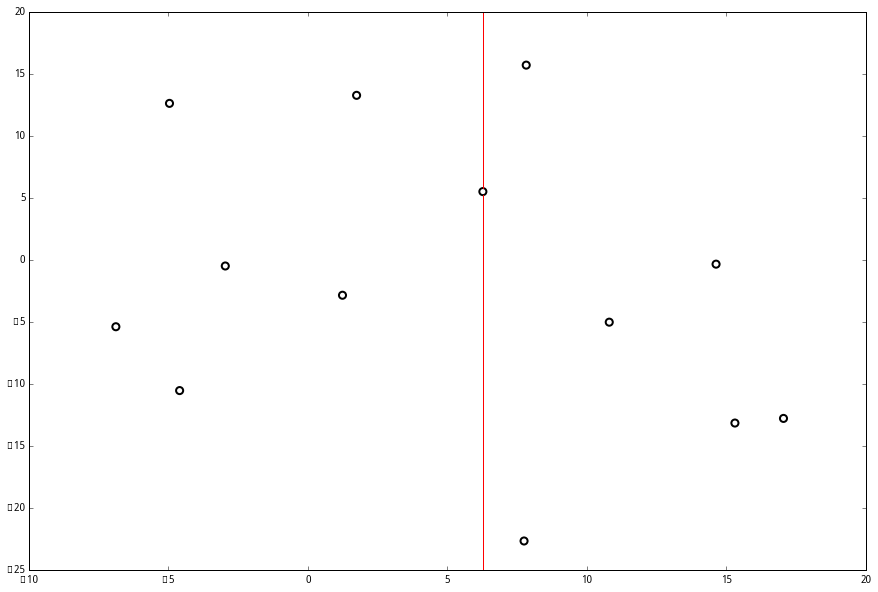

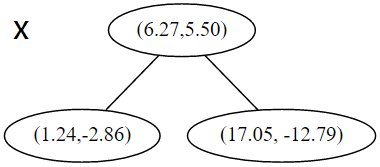
在下一步中 对应 y 轴，左右两边再按照 y 轴的排序进行切分，中位点记载于左右枝的节点。得到下面的树，左边的 x 是指这该层的节点都是沿 x 轴进行分割的。

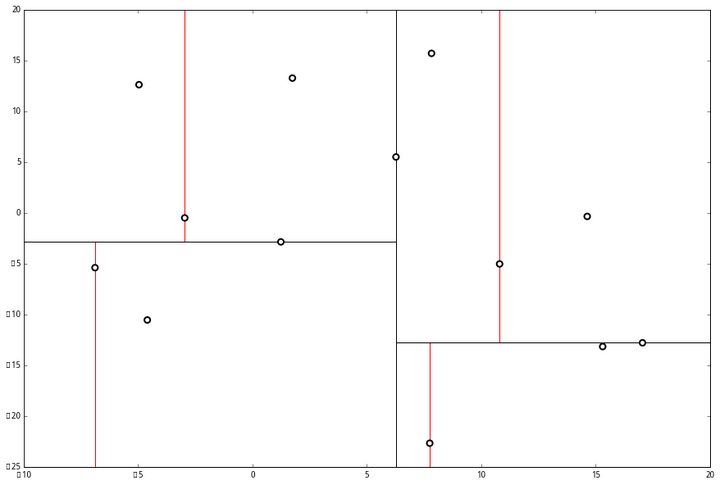
空间的切分如下

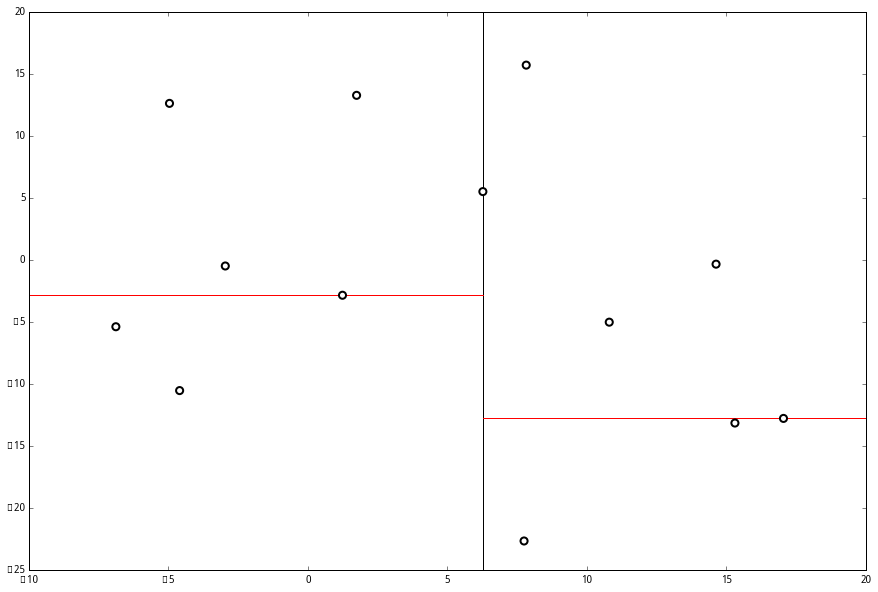
下一步中 r≡1+1≡0 mod 2，对应 x 轴，所以下面再按照 x 坐标进行排序和切分，有

最后每一部分都只剩一个点，将他们记在最底部的节点中。因为不再有未被记录的点，所以不再进行切分。

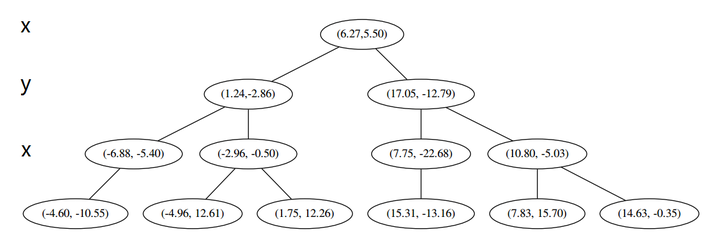
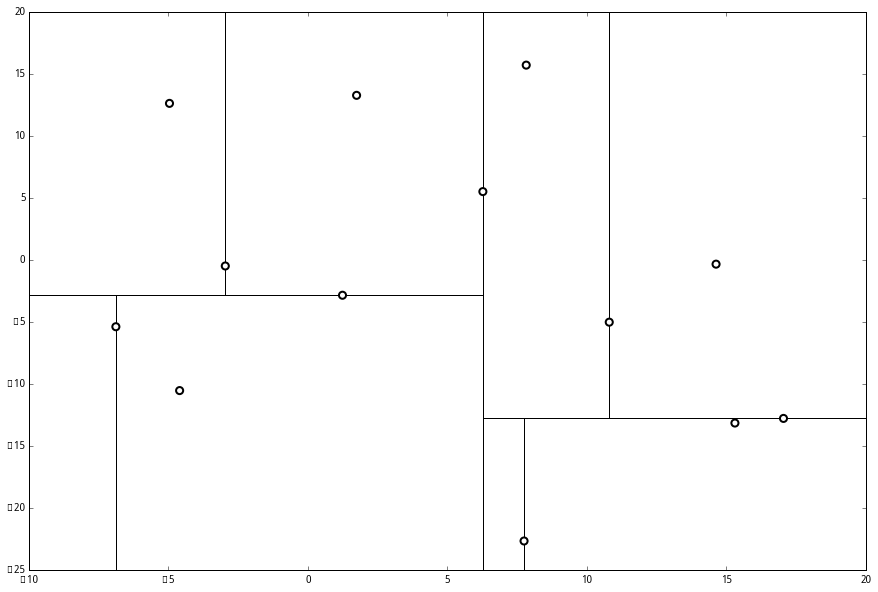就此完成了 kd 树的构造。

kd 树上的 kNN 算法

给定一个构建于一个样本集的 kd 树，下面的算法可以寻找距离某个点 p 最近的 k 个样本。

零、设 L 为一个有 k 个空位的列表，用于保存已搜寻到的最近点。
一、根据 p 的坐标值和每个节点的切分向下搜索（也就是说，如果树的节点是照 进行切分，并且 p 的 r 坐标小于 a，则向左枝进行搜索；反之则走右枝）。
二、当达到一个底部节点时，将其标记为访问过。如果 L 里不足 k 个点，则将当前节点的特征坐标加入 L ；如果 L 不为空并且当前节点的特征与 p 的距离小于 L 里最长的距离，则用当前特征替换掉 L 中离 p 最远的点。
三、如果当前节点不是整棵树最顶端节点，执行 (a)；反之，输出 L，算法完成。
a. 向上爬一个节点。如果当前（向上爬之后的）节点未曾被访问过，将其标记为被访问过，然后执行 (1) 和 (2)；如果当前节点被访问过，再次执行 (a)。
1. 如果此时 L 里不足 kk 个点，则将节点特征加入 L；如果 L 中已满 k 个点，且当前节点与 p 的距离小于 L 里最长的距离，则用节点特征替换掉 L 中离最远的点。
2.
计算 p 和当前节点切分线的距离。如果该距离大于等于 L 中距离 p 最远的距离并且 L 中已有 k
个点，则在切分线另一边不会有更近的点，执行 (三)；如果该距离小于 L 中最远的距离或者 L 中不足 k
个点，则切分线另一边可能有更近的点，因此在当前节点的另一个枝从 (一) 开始执行。

啊呃… 被这算法噎住了，赶紧喝一口下面的例子

设我们想查询的点为 p=(−1,−5)，设距离函数是普通的 距离，我们想找距离问题点最近的 k=3 个点。如下：

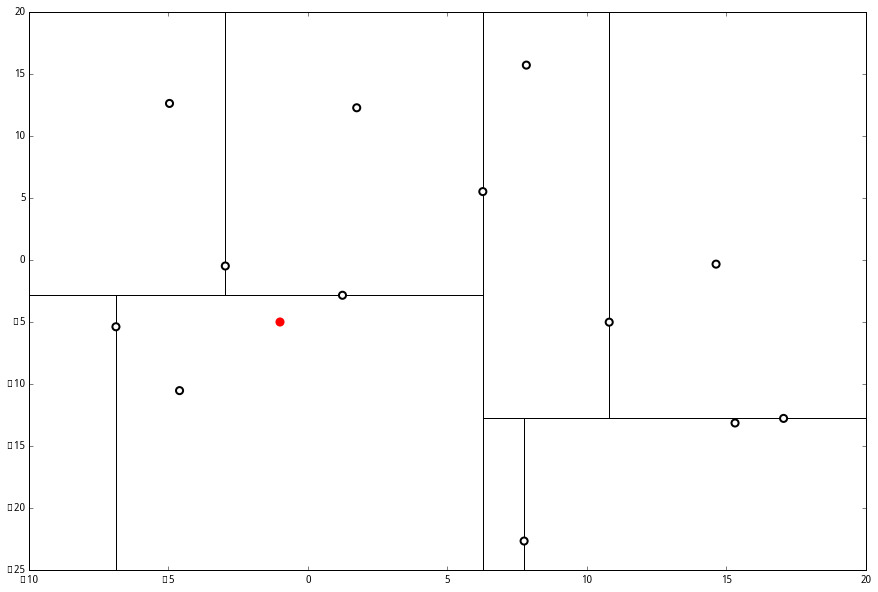
首先执行 (一)，我们按照切分找到最底部节点。首先，我们在顶部开始

和这个节点的 x 轴比较一下，
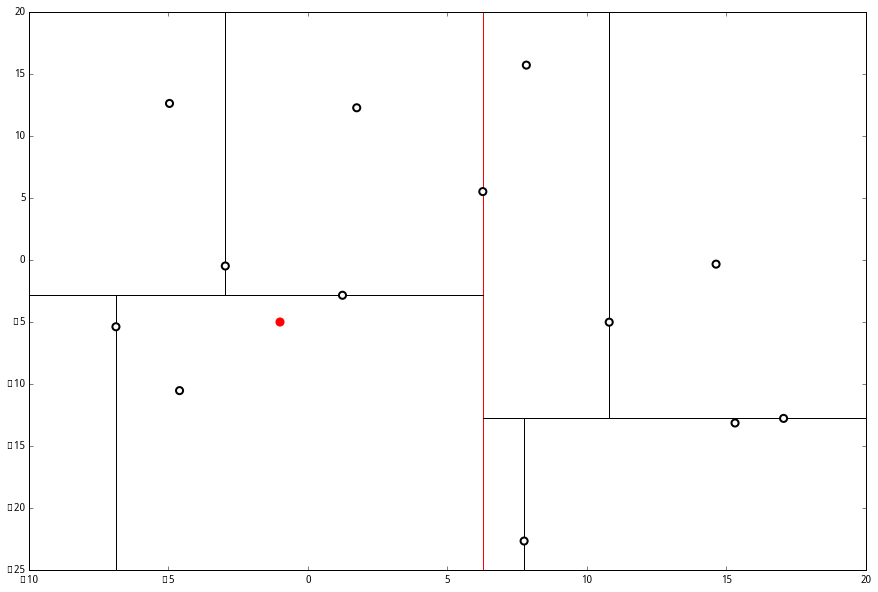p 的 x 轴更小。因此我们向左枝进行搜索：
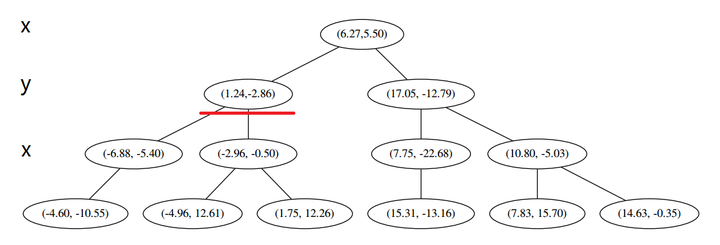这次对比 y 轴，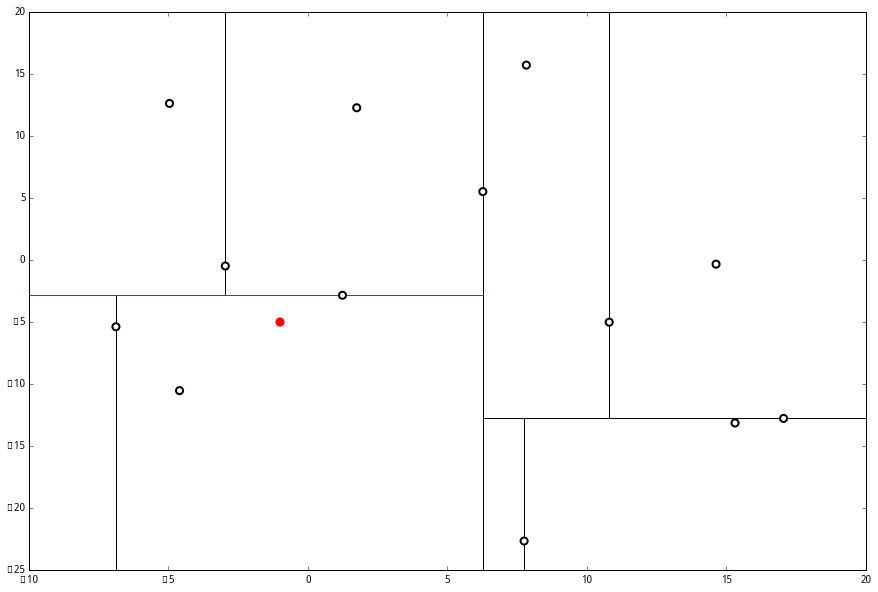

p 的 y 值更小，因此向左枝进行搜索：

这个节点只有一个子枝，就不需要对比了。由此找到了最底部的节点 (−4.6,−10.55)。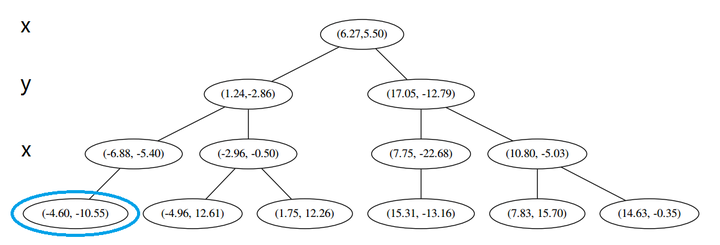
在二维图上是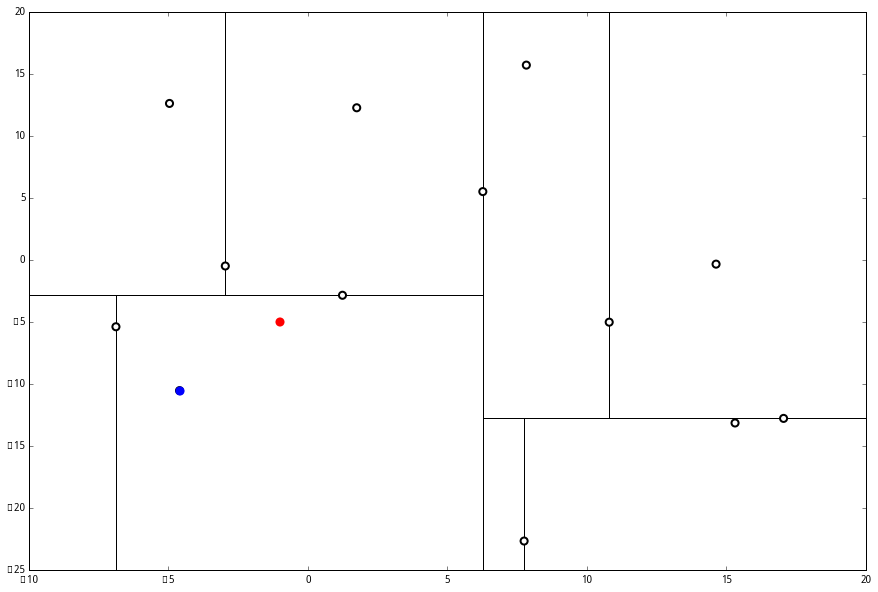

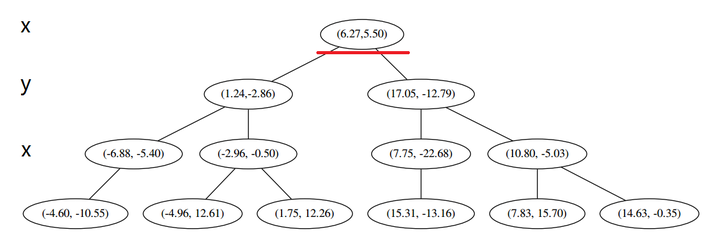
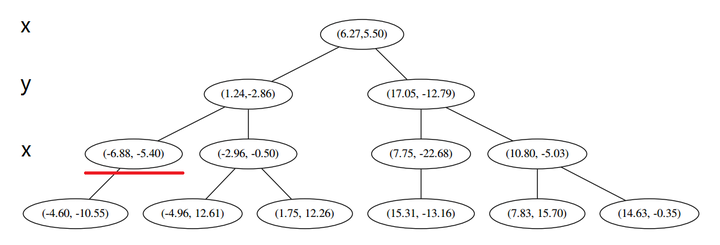
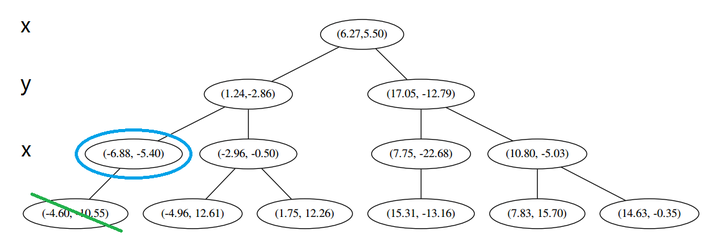
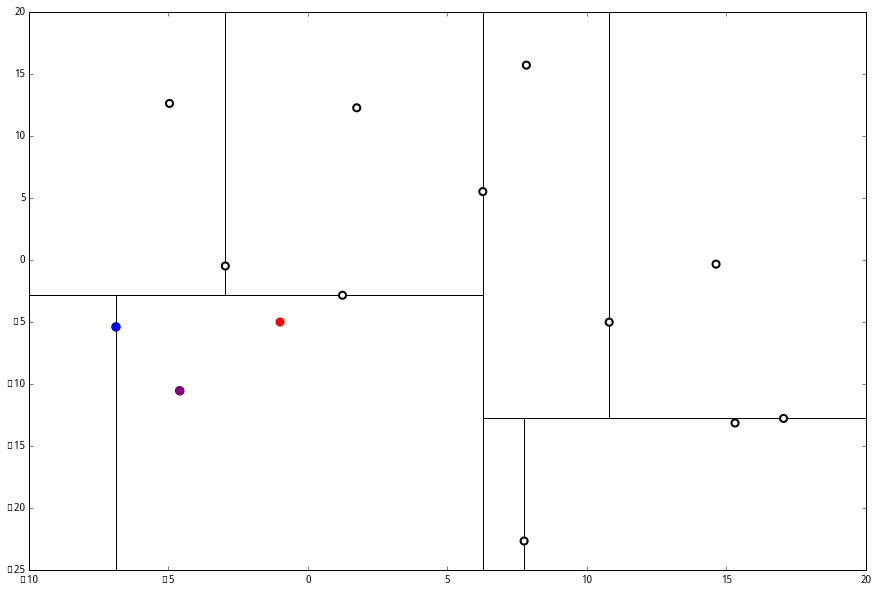
此时我们执行 (二)。将当前结点标记为访问过，并记录下 L=[(−4.6,−10.55)]。啊，访问过的节点就在二叉树上显示为被划掉的好了。

然后执行 (三)，嗯，不是最顶端节点。好，执行 (a)，我爬。上面的是 (−6.88,−5.4)。

执行
(1)，因为我们记录下的点只有一个，小于 k=3，所以也将当前节点记录下，有
L=[(−4.6,−10.55),(−6.88,−5.4)].再执行 (2)，因为当前节点的左枝是空的，所以直接跳过，回到步骤 (三)。(三)
看了一眼，好，不是顶部，交给你了，(a)。于是乎 (a) 又往上爬了一节。

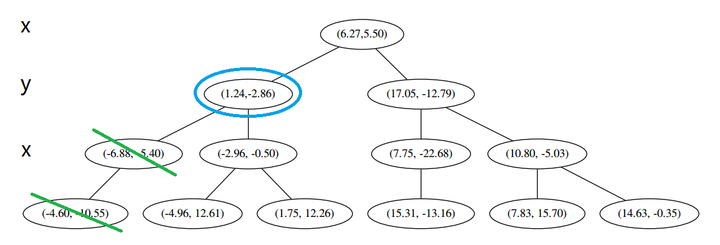
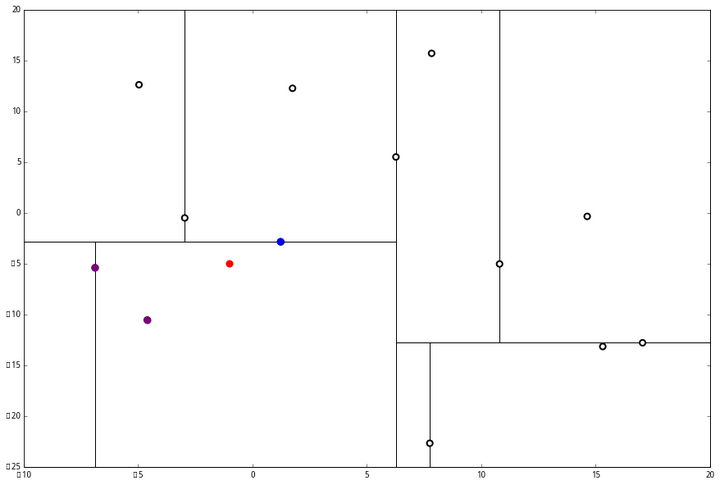
(1) 说，由于还是不够三个点，于是将当前点也记录下，有 L=[(−4.6,−10.55),(−6.88,−5.4),(1.24,−2.86)]。当然，当前结点变为被访问过的。

(2) 又发现，当前节点有其他的分枝，并且经计算得出 p 点和 L 中的三个点的距离分别是 6.62,5.89,3.10，但是 p 和当前节点的分割线的距离只有 2.14，小于与 L 的最大距离：

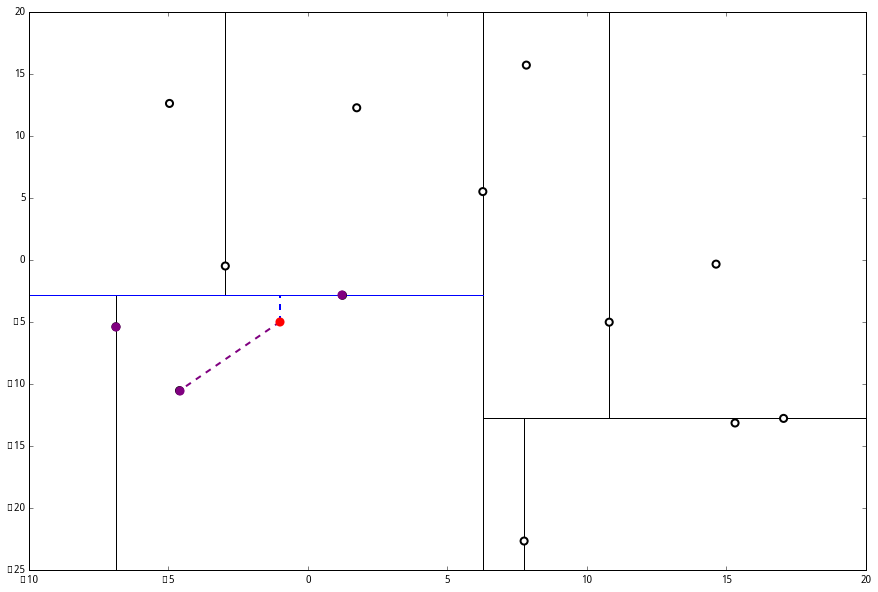
因此，在分割线的另一端可能有更近的点。于是我们在当前结点的另一个分枝从头执行 (一)。好，我们在红线这里：

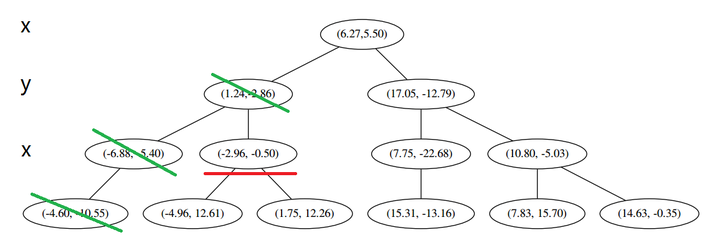
要用 p 和这个节点比较 x 坐标:

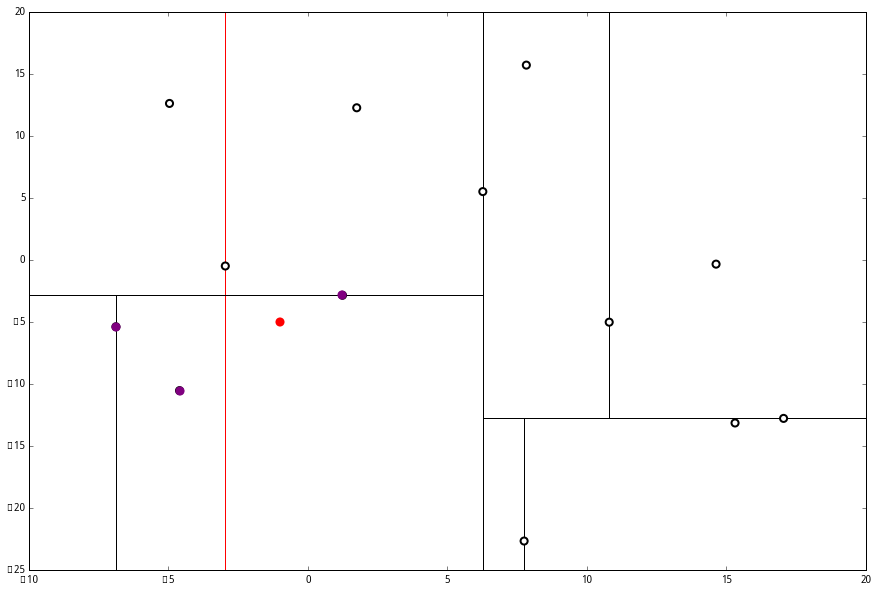p 的 x 坐标更大，因此探索右枝 (1.75,12.26)，并且发现右枝已经是最底部节点，因此启动 (二)。
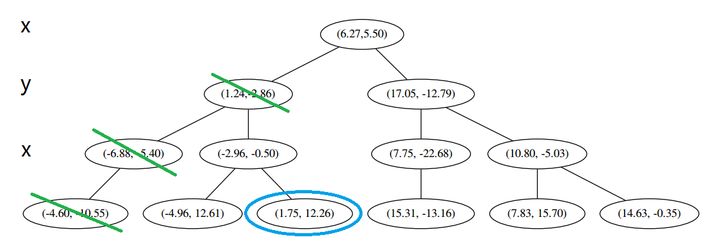经计算，(1.75,12.26) 与 p 的距离是 17.48，要大于 p 与 L 的距离，因此我们不将其放入记录中。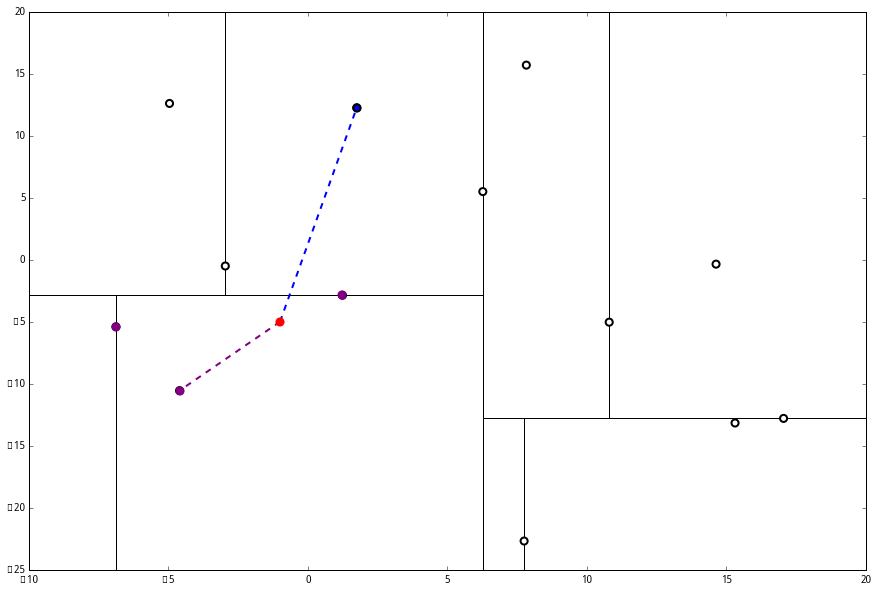

然后 (三) 判断出不是顶端节点，呼出 (a)，爬。

(1) 出来一算，这个节点与 p 的距离是 4.91，要小于 p 与 L 的最大距离 6.62。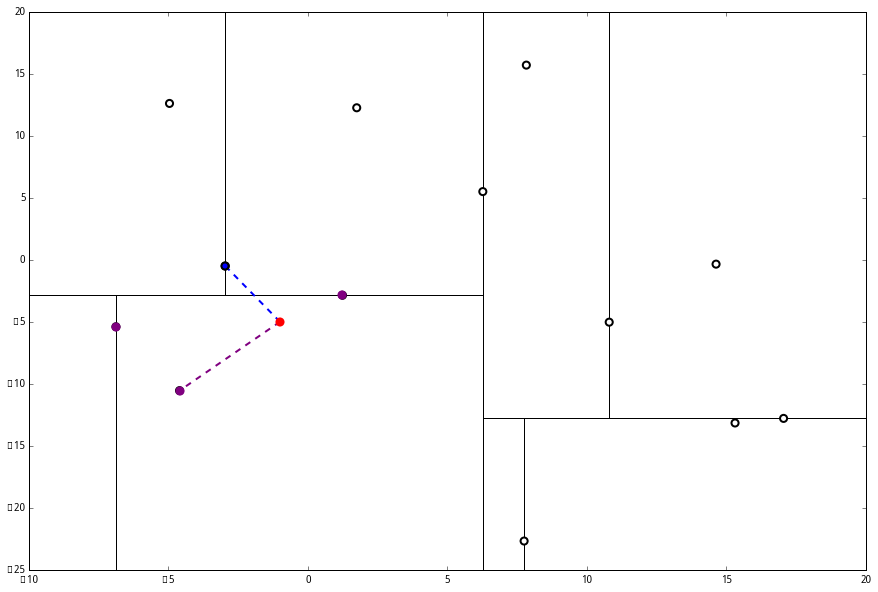

因此，我们用这个新的节点替代 L 中离 p 最远的 (−4.6,−10.55)。

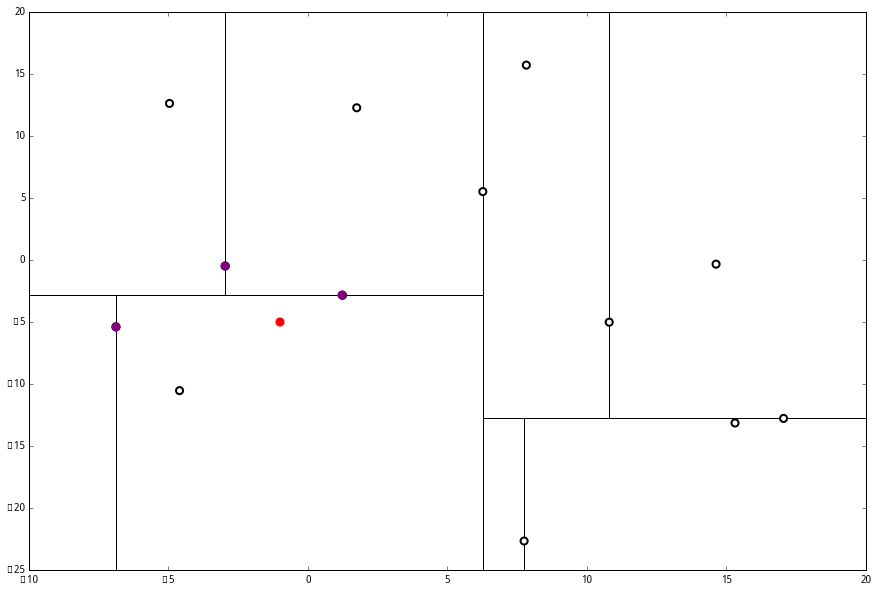
然后 (2) 又来了，我们比对 p 和当前节点的分割线的距离

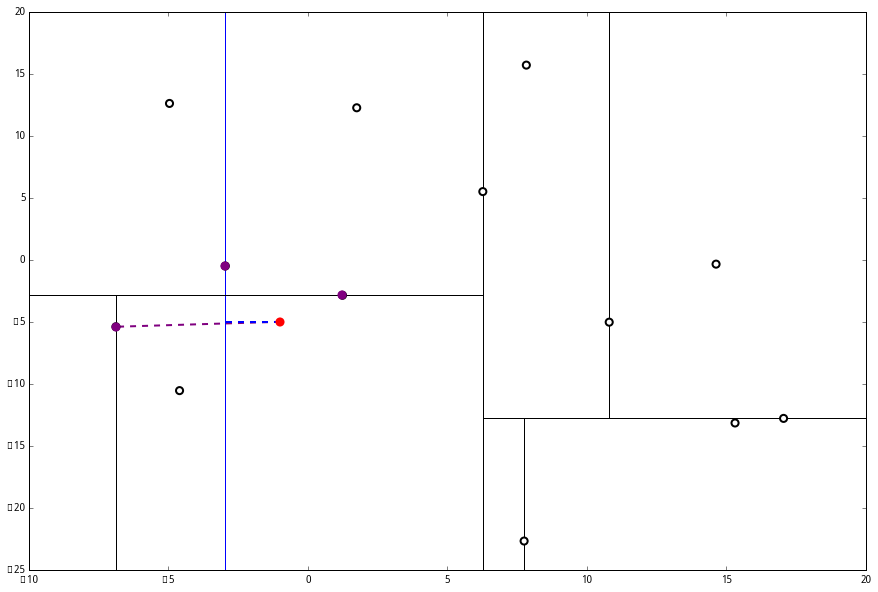
这个距离小于 L 与 p 的最小距离，因此我们要到当前节点的另一个枝执行 (一)。当然，那个枝只有一个点，直接到 (二)。

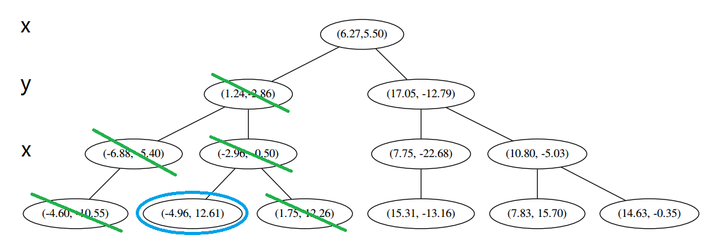
计算距离发现这个点离 p 比 L 更远，因此不进行替代。

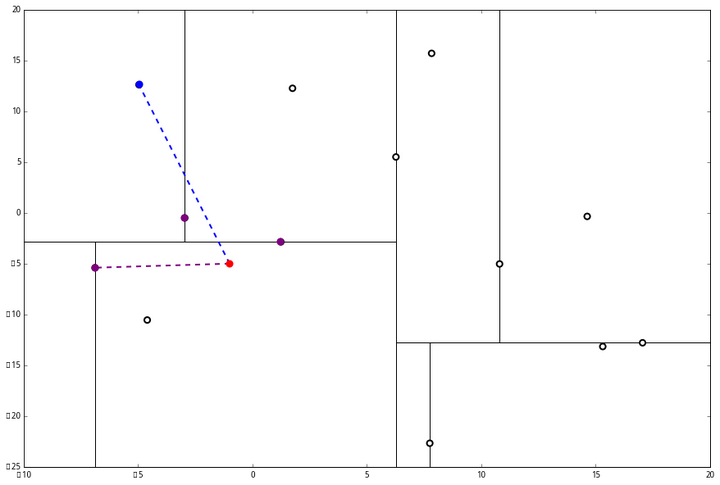
(三) 发现不是顶点，所以呼出 (a)。我们向上爬，

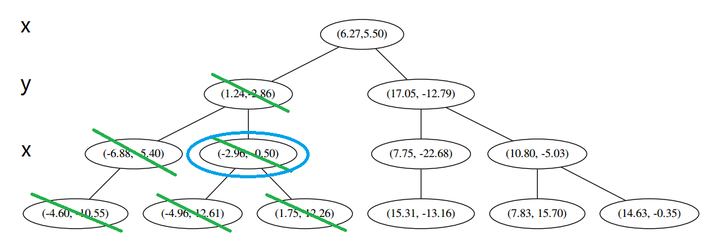
这个是已经访问过的了，所以再来（a），

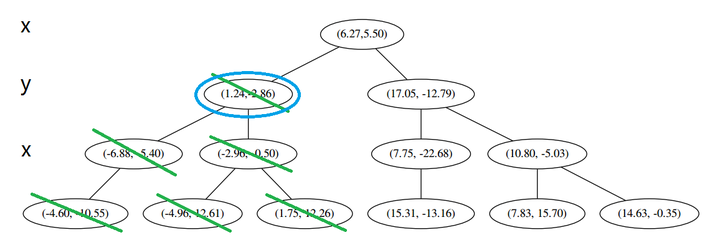
好，（a）再爬，

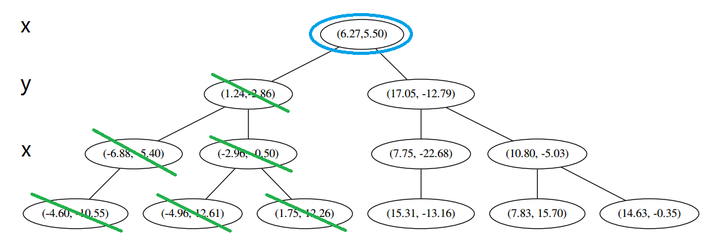
啊！到顶点了。所以完了吗？当然不，还没轮到 (三) 呢。现在是 (1) 的回合。

我们进行计算比对发现顶端节点与p的距离比L还要更远，因此不进行更新。

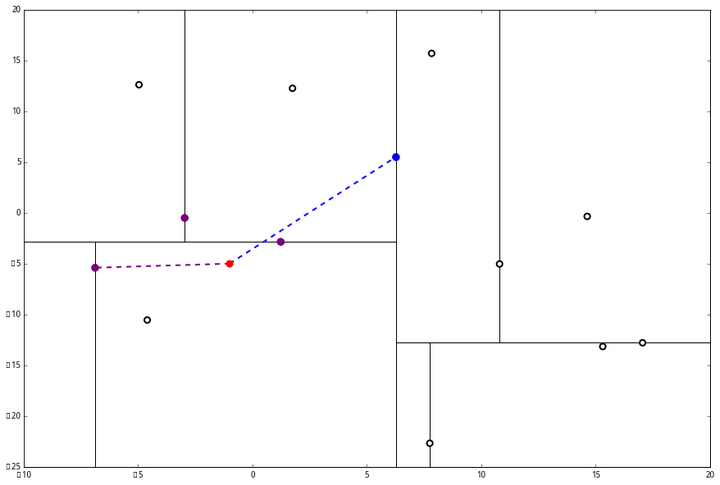
然后是 (2)，计算 p 和分割线的距离发现也是更远。

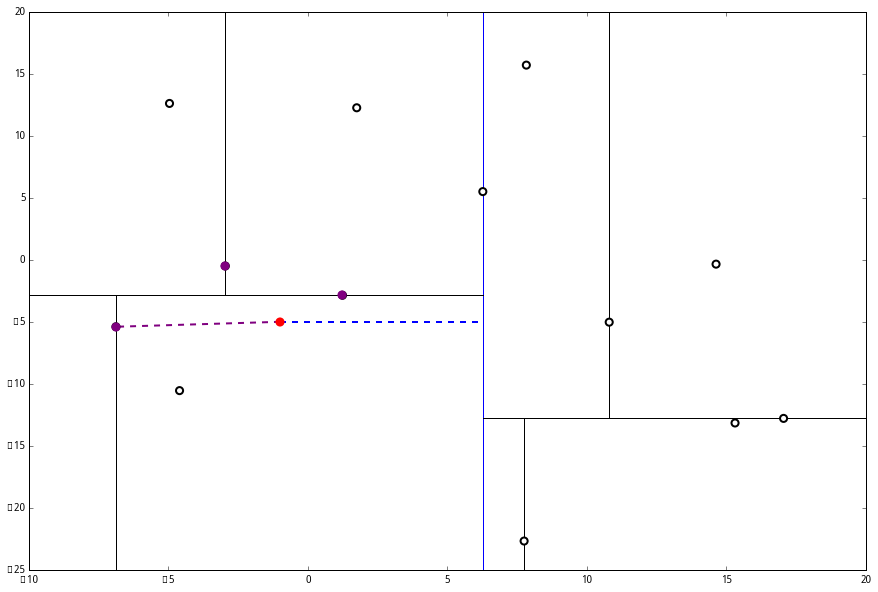
因此也不需要检查另一个分枝。

然后执行 (三)，判断当前节点是顶点，因此计算完成！输出距离 p 最近的三个样本是 L=[(−6.88,−5.4),(1.24,−2.86),(−2.96,−2.5)]。

结语

kd
树的 kNN
算法节约了很大的计算量（虽然这点在少量数据上很难体现），但在理解上偏于复杂，希望本篇中的实例可以让读者清晰地理解这个算法。喜欢动手的读者可以尝试自己用代码实现
kd 树算法，但也可以用现成的机器学习包 scikit-learn 来进行计算。量化课堂的下一篇文章就将讲解如何用 scikit-learn 进行 kNN 分类。