HDU 4311 Meeting point-1 && HDU 4312 Meeting point-2

这俩个题  题意：：给出N(<1e5)个点求找到一个点作为聚会的地方，使每个点到达这里的距离最小。4311是 曼哈顿距离 4312是 切比雪夫距离；

曼哈顿距离 ：大家都知道 对于二维坐标系a(xa,yb),b(xb,yb)的曼哈顿距离是abs（xa-xb）+abs（ya-yb）；

　　看的出来这个距离和x，y 都有关，但是X,Y并不相互影响，所以可以分开计算这样，分开计算的好处如下：

　　如果 只给一个维度的坐标系 ，我们是不可以再什么养的复杂度的时间内处理出来呢？ 大难还是很好想的先排序一下，会发现就需要O（n）的时间就可以算出来我们想要的答案

　　至于俩个维度的合并运算只要O（N）记录就可以了；

切比雪夫距离：

　　我们知道对于距离一个点的曼哈顿距离为R 的点可以形成一个正方形如下图：

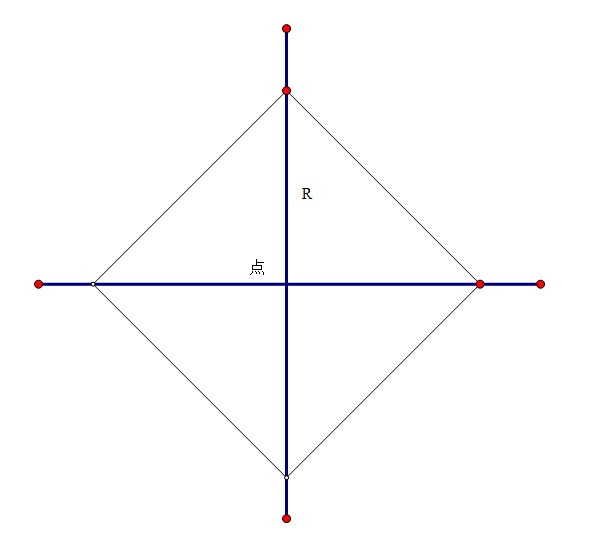
　　也知道对于距离一个点的切比雪夫距离为R 的点也可以形成一个正方形如下图：

　　　

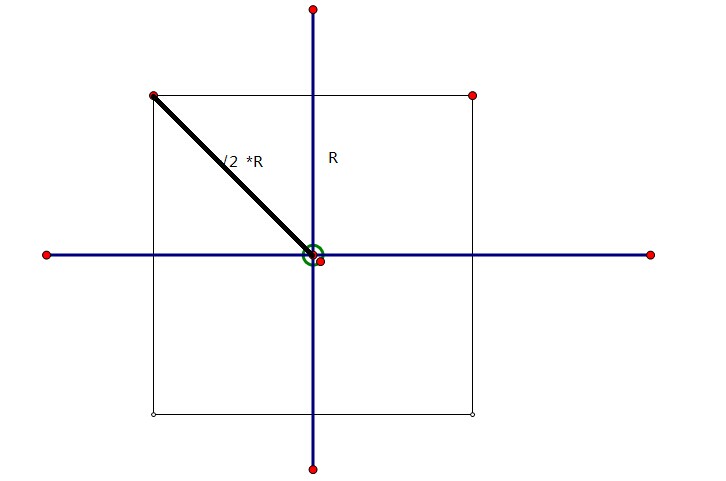
　　对比俩个图片我们知道：距离一个点的 切比雪夫距离可以通过一定的变换转换成 曼哈顿距离（因为曼哈顿距离怎么算我们上面已经讲过了）！！！；

　　比较麻烦？：但其实很简单：我们知道上面的 切比雪夫的正方形 旋转45度 在变换一定的倍数会 和 曼哈顿的正方形重合！所以我饿们可以认为 切比雪夫距离是  曼哈顿距离旋转在放大的结果：反过来只要对坐标进行同样的旋转和放大就可以了；

代码如下：：：

#include <cstdio>
#include <map>
#include <vector>
#include <set>
#include <iostream>
using namespace std;
typedef long long LL;
struct info
{
    LL x,y;
    int cnt;
    info(){}
    info(int x,int y):x(x),y(y){}
};
bool cmpx(info  a,info b)
{
    if(a.x==b.x)return a.y<b.y;
    return a.x<b.x;
}
bool cmpy(info a,info b)
{
    if(a.y==b.y) return a.x<b.x;
    return a.y<b.y;
}
info ko1[];
info ko2[];
LL dp1[];
LL dp2[];
int n;
void make(int x)
{
    int tmpx,tmpy;
    tmpx=ko1[x].x;
    tmpy=ko1[x].y;
//这么写是按远点点进行逆时针旋转的
//你也可以按别的点进行旋转  不过们的旋转点必须是一个
//列
//tmpx=ko1[x].x-2;
//tmpy=ko1[x].y+12;
    ko1[x].x=tmpx-tmpy;
    ko1[x].y=tmpy+tmpx;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(int i=;i<=n;i++)
        {
           // cin>>ko1[i].x>>ko1[i].y;
            scanf("%I64d%I64d",&ko1[i].x,&ko1[i].y);
            make(i);//有这句是12 没这句是11
        }
        sort(ko1+,ko1++n,cmpx);
        for(int i=;i<=n;i++)
        {
            ko1[i].cnt=i;
            ko2[i]=ko1[i];
        }
        sort(ko2+,ko2++n,cmpy);
        for(int i=;i<=n;i++)
        {
            dp1[i]=dp1[i-]+abs(ko1[i].x-ko1[].x);
            dp2[i]=dp2[i-]+abs(ko2[i].y-ko2[].y);
        }
        LL ans=1LL<<;
        for(int i=;i<=n;i++)
        {
            LL tmp2=dp2[n]-dp2[i]-(ko2[i].y-ko2[].y)*(n-i)+(ko2[i].y-ko2[].y)*i-dp2[i];
            int cnt=ko2[i].cnt;
            LL tmp1=dp1[n]-dp1[cnt]-(ko1[cnt].x-ko1[].x)*(n-cnt)+(ko1[cnt].x-ko1[].x)*cnt-dp1[cnt];
            ans=min(ans,(tmp1+tmp2)/);//  这个12 要除以2；11不需要
        }
        cout<<ans<<endl;
    }
    return ;
}