C语言---魔方阵

魔方阵的定义：在n*n的方阵中，每一行的和=每一列的和=对角线的和。（本文中涉及的n为大于3的奇数）。

例如3*3的魔方阵为：

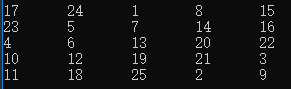
5*5的魔方阵为：

如何写魔方阵呢？

1.数字1位于第一行的正中间
2.下一个数放到上一个数的右上角（即上一行下一列），若无上一行则放到最后一行，若无下一列则放到第一列
3.若新位置已经放了数，则将其放入该数的正下方（即下一行的同一列）

b站讲解视频：https://www.bilibili.com/video/BV1HU4y1f7AD?spm_id_from=333.788.top_right_bar_window_dynamic.content.click

C语言代码：

 1 int magicMatrix() {
 2     printf("请输入你想生成的魔方阵阶数：（大于3的奇数）\n");
 3     int i,c,r;
 4     scanf("%d",&i);
 5     int arr[i][i];
 6     for(int n=0; n<i; n++) {
 7         for(int m=0; m<i; m++) {
 8             arr[n][m]=0;
 9         }
10     }
11     c=0;
12     r=i/2;
13     arr[c][r] = 1;// 魔方阵的第一行最中间的数为1
14     int k=i*i;
15     for(int j=2; j<=k; j++) {
16         int h=c,l=r;         //记录原来的位置
17         if(c==0) {
18             c=i-1;
19         } else {
20             c=c-1;
21         }
22         if(r==i-1) {
23             r=0;
24         } else {
25             r=r+1;
26         }
27         if(arr[c][r]!=0) {
28             c=h+1;
29             r=l;
30         }
31         printf("c=%d,r=%d,j=%d\n",c,r,j);
32         arr[c][r]=j;
33     }
34     printf("\n");
35     for(int n=0; n<i; n++) {
36         for(int m=0; m<i; m++) {
37             printf("%d\t",arr[n][m]);
38         }
39         printf("\n");
40     }
41 }

计算下一个数字的位置时，如果位置已经被占，就在该数的下一行同一列，所以代码中每次计算要记录该数的位置。

运行结果为：

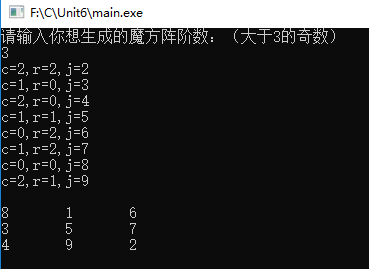
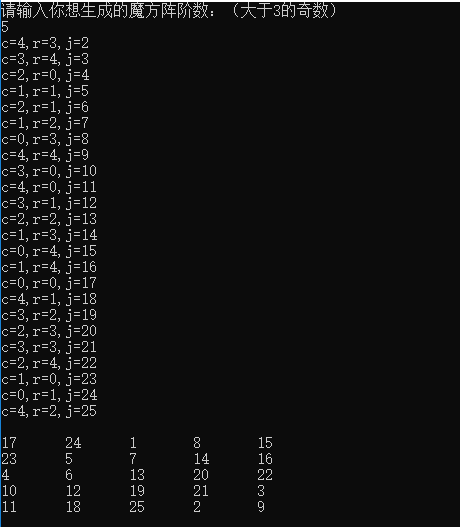
代码没有做错误输入验证，朋友们可以自行加上。