MOEAD实现、基于分解的多目标进化、 切比雪夫方法-（python完整代码）

确定某点附近的点

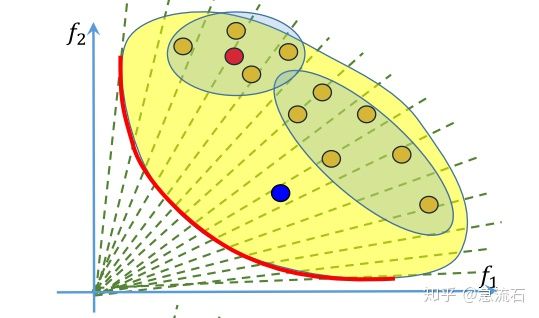
答：每个解对应的是一组权重，即子问题，红点附近的四个点，也就是它的邻居怎么确定呢？由权重来确定，算法初始化阶段就确定了每个权重对应的邻居，也就是每个子问题的邻居子问题。权重的邻居通过欧式距离来判断。取最近的几个。

取均匀分布向量

https://www.cnblogs.com/Twobox/p/16408751.html

MOEAD实现

算法理解与流程

https://www.zhihu.com/question/263555181?sort=created
其中两个回答都挺好的

1. 输入N m
# N表示取点密度 m表示问题维度
1.1 输入 T
# 表示取最近的T个作为邻居
2. 生成均匀分布权重向量
2.1 计算每个权重向量之间的欧拉距离
3. 权重向量个数即为：初始种群个数
4. 初始化种群，每个个体一一对应权重
4.1 更具权重之间距离，取前T个作为邻居person
5. EP = 空
# 维护成最优前沿
6. 计算最初的全局最优Z
# 把每个带入f1 f2中，取最小值 z1 z2
7. 开始循环N代
    7.1对于每个个体，在领域中选取2个个体进行交叉变异，获得2个新个体
    7.1.1更新全局解z
    7.2在领域中随机选择2个个体，用新个与旧个体进行对比
    # 新个体带入子目标问题，直接对比值即可
    7.3如果更优，则替换旧个体dna
    7.4更新EP
    # 如果有别接收的新解，将新解与EP每一个进行比较，删除被新解支配的，如果新解没有被旧解支配，那么加入EP

代码实现设计

# 分析
需要维护的数据结构：
    某个体最近的T位邻居： 可以考虑采用对象列表即可
    均匀分布的权重向量：一个二维ndarray数组即可
    权重向量与个体对应关系：个体对象，直接保存权重向量数组
    权重向量之间的距离矩阵：开局初始化，不变的
    EP list,里面的个体是对象的引用
    z list
    目标函数集合，F list domain list

# 接口设计
class Person
    attribute:
        dns：一维ndarray
        weight_vector: 一维ndarray
        neighbor: list<Person>
        o_func:Objective_Function 目标函数
    function:
        mutation
        cross_get_two_new_dna：返回2段新dna
        compare#与子代比较
        accept_new_dna
        choice_two_person:p1,p2
​
class Moead_Util
    attribute:
        N
        M
        T:
        o_func：Objective_Function
        pm:变异概率

        EP:[dna1,dna2,..]
        weight_vectors:二维数组
        Euler_distance:二维数组
        pip_size
        Z:[] # 这里面元素为一维ndarray数组，即dna，即解

    function:
        init_mean_vector:二维数组
        init_Euler_distance:二维数组
        init_population:[]
        init_Z:一维属猪

        update_ep
        update_Z

class Objective_Function:
    attribute:
        F:[]
        domain:[[0，1],[],[]]
    function:
        get_one_function:Objective_Function

Person.py

 1 import numpy as np
 2
 3
 4 class Person:
 5     def __init__(self, dna):
 6         self.dna = dna
 7         self.weight_vector = None
 8         self.neighbor = None
 9         self.o_func = None  # 目标函数
10
11         self.dns_len = len(dna)
12
13     def set_info(self, weight_vector, neighbor, o_func):
14         self.weight_vector = weight_vector
15         self.neighbor = neighbor
16         self.o_func = o_func# 目标函数
17
18     def mutation_dna(self, one_dna):
19         i = np.random.randint(0, self.dns_len)
20         low = self.o_func.domain[i][0]
21         high = self.o_func.domain[i][1]
22         new_v = np.random.rand() * (high - low) + low
23         one_dna[i] = new_v
24         return one_dna
25
26     def mutation(self):
27         i = np.random.randint(0, self.dns_len)
28         low = self.o_func.domain[i][0]
29         high = self.o_func.domain[i][1]
30         new_v = np.random.rand() * (high - low) + low
31         self.dna[i] = new_v
32
33     @staticmethod
34     def cross_get_two_new_dna(p1, p2):
35         # 单点交叉
36         cut_i = np.random.randint(1, p1.dns_len - 1)
37         dna1 = p1.dna.copy()
38         dna2 = p2.dna.copy()
39         temp = dna1[cut_i:].copy()
40         dna1[cut_i:] = dna2[cut_i:]
41         dna2[cut_i:] = temp
42         return dna1, dna2
43
44     def compare(self, son_dna):
45         F = self.o_func.f_funcs
46         f_x_son_dna = []
47         f_x_self = []
48         for f in F:
49             f_x_son_dna.append(f(son_dna))
50             f_x_self.append(f(self.dna))
51         fit_son_dna = np.array(f_x_son_dna) * self.weight_vector
52         fit_self = np.array(f_x_self) * self.weight_vector
53         return fit_son_dna.sum() - fit_self.sum()
54
55     def accept_new_dna(self, new_dna):
56         self.dna = new_dna
57
58     def choice_two_person(self):
59         neighbor = self.neighbor
60         neighbor_len = len(neighbor)
61         idx = np.random.randint(0, neighbor_len, size=2)
62         p1 = self.neighbor[idx[0]]
63         p2 = self.neighbor[idx[1]]
64         return p1, p2

Objective_Function

 1 from collections import defaultdict
 2
 3 import numpy as np
 4
 5
 6 def zdt4_f1(x_list):
 7     return x_list[0]
 8
 9
10 def zdt4_gx(x_list):
11     sum = 1 + 10 * (10 - 1)
12     for i in range(1, 10):
13         sum += x_list[i] ** 2 - 10 * np.cos(4 * np.pi * x_list[i])
14     return sum
15
16
17 def zdt4_f2(x_list):
18     gx_ans = zdt4_gx(x_list)
19     if x_list[0] < 0:
20         print("????: x_list[0] < 0:", x_list[0])
21     if gx_ans < 0:
22         print("gx_ans < 0", gx_ans)
23     if (x_list[0] / gx_ans) <= 0:
24         print("x_list[0] / gx_ans<0：", x_list[0] / gx_ans)
25
26     ans = 1 - np.sqrt(x_list[0] / gx_ans)
27     return ans
28
29 def zdt3_f1(x):
30     return x[0]
31
32
33 def zdt3_gx(x):
34     if x[:].sum() < 0:
35         print(x[1:].sum(), x[1:])
36     ans = 1 + 9 / 29 * x[1:].sum()
37     return ans
38
39
40 def zdt3_f2(x):
41     g = zdt3_gx(x)
42     ans = 1 - np.sqrt(x[0] / g) - (x[0] / g) * np.sin(10 * np.pi * x[0])
43     return ans
44
45
46 class Objective_Function:
47     function_dic = defaultdict(lambda: None)
48
49     def __init__(self, f_funcs, domain):
50         self.f_funcs = f_funcs
51         self.domain = domain
52
53     @staticmethod
54     def get_one_function(name):
55         if Objective_Function.function_dic[name] is not None:
56             return Objective_Function.function_dic[name]
57
58         if name == "zdt4":
59             f_funcs = [zdt4_f1, zdt4_f2]
60             domain = [[0, 1]]
61             for i in range(9):
62                 domain.append([-5, 5])
63             Objective_Function.function_dic[name] = Objective_Function(f_funcs, domain)
64             return Objective_Function.function_dic[name]
65
66         if name == "zdt3":
67             f_funcs = [zdt3_f1, zdt3_f2]
68             domain = [[0, 1] for i in range(30)]
69             Objective_Function.function_dic[name] = Objective_Function(f_funcs, domain)
70             return Objective_Function.function_dic[name]

Moead_Util.py

  1 import numpy as np
  2
  3 from GA.MOEAD.Person import Person
  4
  5
  6 def distribution_number(sum, m):
  7     # 取m个数，数的和为N
  8     if m == 1:
  9         return [[sum]]
 10     vectors = []
 11     for i in range(1, sum - (m - 1) + 1):
 12         right_vec = distribution_number(sum - i, m - 1)
 13         a = [i]
 14         for item in right_vec:
 15             vectors.append(a + item)
 16     return vectors
 17
 18
 19 class Moead_Util:
 20     def __init__(self, N, m, T, o_func, pm):
 21         self.N = N
 22         self.m = m
 23         self.T = T  # 邻居大小限制
 24         self.o_func = o_func
 25         self.pm = pm  # 变异概率
 26
 27         self.Z = np.zeros(shape=m)
 28
 29         self.EP = []  # 前沿
 30         self.EP_fx = []  # ep对应的目标值
 31         self.weight_vectors = None  # 均匀权重向量
 32         self.Euler_distance = None  # 欧拉距离矩阵
 33         self.pip_size = -1
 34
 35         self.pop = None
 36         # self.pop_dna = None
 37
 38     def init_mean_vector(self):
 39         vectors = distribution_number(self.N + self.m, self.m)
 40         vectors = (np.array(vectors) - 1) / self.N
 41         self.weight_vectors = vectors
 42         self.pip_size = len(vectors)
 43         return vectors
 44
 45     def init_Euler_distance(self):
 46         vectors = self.weight_vectors
 47         v_len = len(vectors)
 48
 49         Euler_distance = np.zeros((v_len, v_len))
 50         for i in range(v_len):
 51             for j in range(v_len):
 52                 distance = ((vectors[i] - vectors[j]) ** 2).sum()
 53                 Euler_distance[i][j] = distance
 54
 55         self.Euler_distance = Euler_distance
 56         return Euler_distance
 57
 58     def init_population(self):
 59         pop_size = self.pip_size
 60         dna_len = len(self.o_func.domain)
 61         pop = []
 62         pop_dna = np.random.random(size=(pop_size, dna_len))
 63         # 初始个体的 dna
 64         for i in range(pop_size):
 65             pop.append(Person(pop_dna[i]))
 66
 67         # 初始个体的 weight_vector, neighbor, o_func
 68         for i in range(pop_size):
 69             # weight_vector, neighbor, o_func
 70             person = pop[i]
 71             distance = self.Euler_distance[i]
 72             sort_arg = np.argsort(distance)
 73             weight_vector = self.weight_vectors[i]
 74             # neighbor = pop[sort_arg][:self.T]
 75             neighbor = []
 76             for i in range(self.T):
 77                 neighbor.append(pop[sort_arg[i]])
 78
 79             o_func = self.o_func
 80             person.set_info(weight_vector, neighbor, o_func)
 81         self.pop = pop
 82         # self.pop_dna = pop_dna
 83
 84         return pop
 85
 86     def init_Z(self):
 87         Z = np.full(shape=self.m, fill_value=float("inf"))
 88         for person in self.pop:
 89             for i in range(len(self.o_func.f_funcs)):
 90                 f = self.o_func.f_funcs[i]
 91                 # f_x_i：某个体，在第i目标上的值
 92                 f_x_i = f(person.dna)
 93                 if f_x_i < Z[i]:
 94                     Z[i] = f_x_i
 95
 96         self.Z = Z
 97
 98     def get_fx(self, dna):
 99         fx = []
100         for f in self.o_func.f_funcs:
101             fx.append(f(dna))
102         return fx
103
104     def update_ep(self, new_dna):
105         # 将新解与EP每一个进行比较，删除被新解支配的
106         # 如果新解没有被旧解支配，则保留
107         new_dna_fx = self.get_fx(new_dna)
108         accept_new = True  # 是否将新解加入EP
109         # print(f"准备开始循环: EP长度{len(self.EP)}")
110         for i in range(len(self.EP) - 1, -1, -1):  # 从后往前遍历
111             old_ep_item = self.EP[i]
112             old_fx = self.EP_fx[i]
113             # old_fx = self.get_fx(old_ep_item)
114             a_b = True  # 老支配行
115             b_a = True  # 新支配老
116             for j in range(len(self.o_func.f_funcs)):
117                 if old_fx[j] < new_dna_fx[j]:
118                     b_a = False
119                 if old_fx[j] > new_dna_fx[j]:
120                     a_b = False
121             # T T : fx相等      直接不改变EP
122             # T F ：老支配新     留老，一定不要新，结束循环.
123             # F T ：新支配老     留新，一定不要这个老，继续循环
124             # F F : 非支配关系   不操作，循环下一个
125             # TF为什么结束循环，FT为什么继续循环，你们可以琢磨下
126             if a_b:
127                 accept_new = False
128                 break
129             if not a_b and b_a:
130                 if len(self.EP) <= i:
131                     print(len(self.EP), i)
132                 del self.EP[i]
133                 del self.EP_fx[i]
134                 continue
135
136         if accept_new:
137             self.EP.append(new_dna)
138             self.EP_fx.append(new_dna_fx)
139         return self.EP, self.EP_fx
140
141     def update_Z(self, new_dna):
142         new_dna_fx = self.get_fx(new_dna)
143         Z = self.Z
144         for i in range(len(self.o_func.f_funcs)):
145             if new_dna_fx[i] < Z[i]:
146                 Z[i] = new_dna_fx[i]
147         return Z

实现.py

import random

import numpy as np

from GA.MOEAD.Moead_Util import Moead_Util
from GA.MOEAD.Objective_Function import Objective_Function
from GA.MOEAD.Person import Person

import matplotlib.pyplot as plt

def draw(x, y):
    plt.scatter(x, y, s=10, c="grey")  # s 点的大小  c 点的颜色 alpha 透明度
    plt.show()

iterations = 1000  # 迭代次数
N = 400
m = 2
T = 40
o_func = Objective_Function.get_one_function("zdt3")
pm = 0.5

moead = Moead_Util(N, m, T, o_func, pm)

moead.init_mean_vector()
moead.init_Euler_distance()
pop = moead.init_population()
moead.init_Z()

for i in range(iterations):
    print(i, len(moead.EP))
    for person in pop:
        p1, p2 = person.choice_two_person()
        d1, d2 = Person.cross_get_two_new_dna(p1, p2)

        if np.random.rand() < pm:
            p1.mutation_dna(d1)
        if np.random.rand() < pm:
            p1.mutation_dna(d2)

        moead.update_Z(d1)
        moead.update_Z(d2)
        t1, t2 = person.choice_two_person()
        if t1.compare(d1) < 0:
            t1.accept_new_dna(d1)
            moead.update_ep(d1)
        if t2.compare(d1) < 0:
            t2.accept_new_dna(d2)
            moead.update_ep(d1)

# 输出结果画图
EP_fx = np.array(moead.EP_fx)

x = EP_fx[:, 0]
y = EP_fx[:, 1]
draw(x, y)

效果-ZDT4

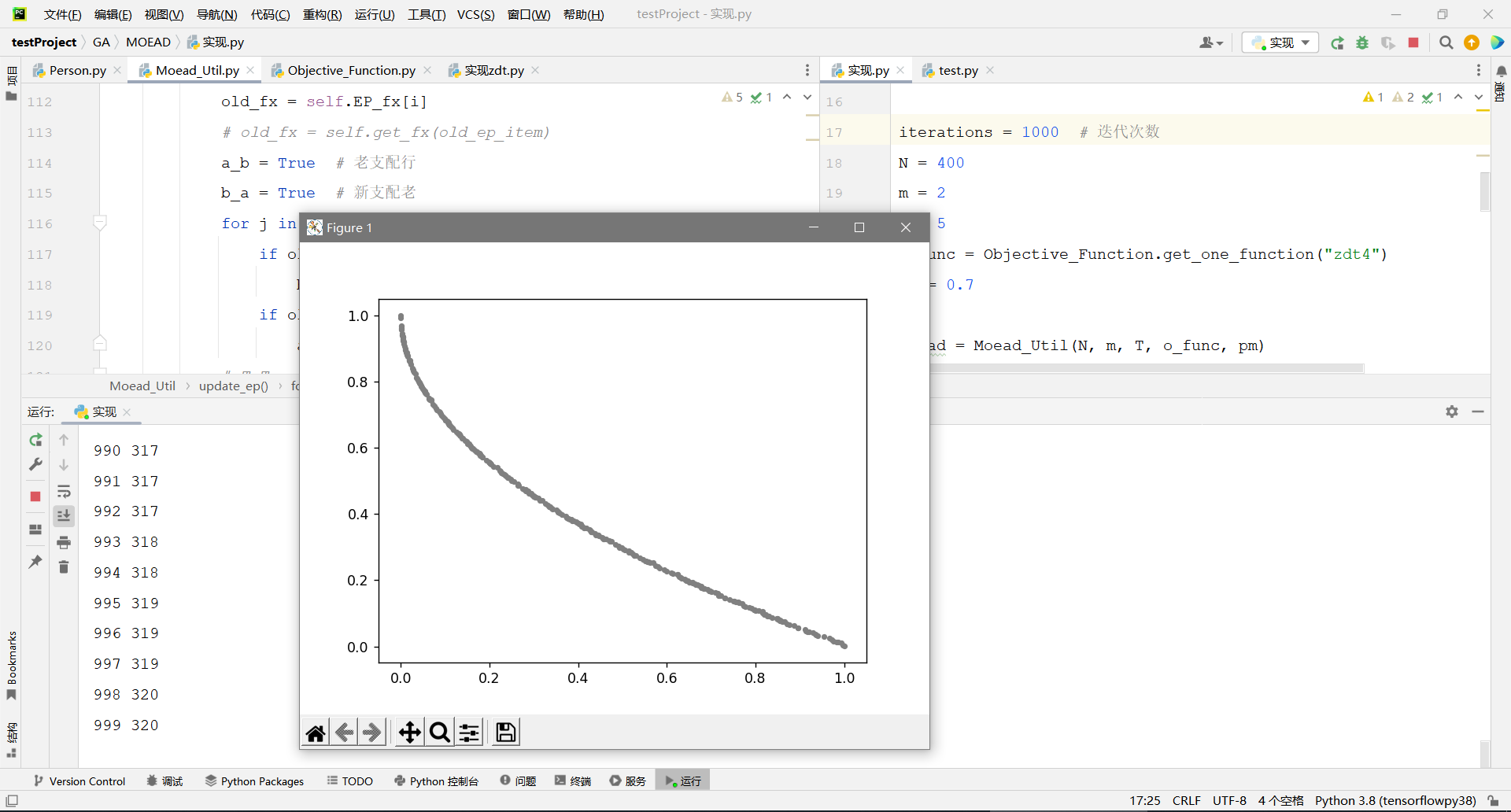
本文原创作者：湘潭大学-魏雄，未经许可禁止转载