CANN算子：利用迭代器高效实现Tensor数据切割分块处理

摘要：本文以Diagonal算子为例，介绍并详细讲解如何利用迭代器对n维Tensor进行基于位置坐标的大批量数据读取工作。

本文分享自华为云社区《CANN算子：利用迭代器高效实现Tensor数据切割分块处理》，作者： CatherineWang 。

任务场景及目标

在CANN aicpu算子开发实现中，经常需要对n维Tensor进行切片（slice）、切块（dice）、转置（transpose）、交换指定维度数据（shuffle）等操作。上述操作实质上是按照指定规律依次进行数据读取，并将读取到的数据写入新的数据地址中。

本文以Diagonal算子为例，介绍并详细讲解如何利用迭代器对n维Tensor进行基于位置坐标的大批量数据读取工作。

Diagonal算子希望对指定两个维度的数据进行对角元素的提取，最终返回张量的对角线元素。本质上该算子通过属性dim1和dim2确定一个矩阵，返回该矩阵的对角元素（存在偏移量offset），并将其放置在最后一维。非dim1和dim2的维度，将会被当成batch维度处理。

常规方案：

方案一：将shape为s，元素个数为numel的 输入Tensor：x转化为Eigen::Tensor：eigen_x；对eigen_x进行shuffle操作，将dim1和dim2换至倒数第二和倒数第一维；通过reshape操作将eigen_x变化为一个三维Eigen::Tensor：reshape_x，shape=(numel/ s[dim1]/s[dim2]，s[dim1]，s[dim2])；对后两维数据取对角元素，并将最终数据赋值给输出数据地址。注意：由于Eigen::Tensor<typename T, int NumIndices_>不能够动态设置维度，即NumIndices_项必须是一个具体的值，因此需要提前定义对应维度的Eigen::Tensor备用。

方案二：对于一个n维的Tensor，利用n层for循环进行数据的定位读取，并取对角值。

可以看出上述两个方案对动态大小的输入计算实现处理都较为繁琐，需要提前分情况设置对应维度的Eigen::Tensor或是for循环逻辑结构，即存在维数限制。

准备知识及分析

我们知道再AICPU中，对于一个Tensor，我们能够通过GetTensorShape、GetData等函数获得Tensor形状大小、具体数据地址等信息。但我们不能通过位置坐标的形式直接获得指定位置的数据值。

1.步长

首先介绍步长（stride）这一概念（对这部分知识已掌握的可以直接跳转下一部分内容）。stride是在指定维度dim中从一个元素跳到下一个元素所必需的步长。例如，对于一个shape=(2, 3, 4, 5)的Tensor，其stride=(60, 20, 5, 1)。因此如果想要获取到上述Tensor中位置坐标为[1, 2, 1, 3]的数据，只需要找到数据地址中第108(=60*1+20*2+5*1+3)位对应值。

2.迭代器

定义迭代器PositionIterator，包含私有成员pos_和shape_，其中pos_为初始位置，shape_为标准形状。通过重载++符号，对pos_进行修改，实现迭代器的自增操作。基于上述迭代器，可以实现对给定的shape依次取位操作。如给定对于给定的shape=(d_1,d_2,…,d_n)，从初始位置(0,0,…,0)开始，依次取(0,0,…,0,0), (0,0,…,0,1),…,(0,0,…,0,d_n-1), (0,0,…,1,0), (0,0,…,1,1),…, (d_1 - 1,d_2 - 1,…,d_{n-1}-1,d_{n}-1).

事实上，可以将上述迭代器理解为一种进制，对于给定的标准形状shape_=(d_1,d_2,…,d_n)，第i位运算时便是逢d_i进1。同时通过PositionIterator .End()控制迭代器的结束。具体实现如下：

template <typename T>
class PositionIterator {
 public:
  PositionIterator(){};
  ~PositionIterator(){};
  PositionIterator(std::vector<T> stt, std::vector<T> sh) {
    if (stt.size() != sh.size()) {
      PositionIterator();
    } else {
      for (unsigned int i = 0; i < sh.size(); i++) {
        if (stt[i] >= sh[i]) {
          PositionIterator();
        }
      }
      pos_ = stt;
      shape_ = sh;
    }
  }
  PositionIterator operator++() {
    pos_[shape_.size() - 1] += 1;
    for (unsigned int i = shape_.size() - 1; i > 0; i--) {
      if (pos_[i] / shape_[i] != 0) {
        pos_[i - 1] += pos_[i] / shape_[i];
        pos_[i] = pos_[i] % shape_[i];
      }
    }
    return *this;
  }

  bool End() {
    if (pos_[0] != shape_[0]) {
      return false;
    }
    return true;
  }

  std::vector<T> GetPos() { return pos_; }

  std::vector<T> GetShape() { return shape_; }

 private:
  std::vector<T> pos_;
  std::vector<T> shape_;
};

Diagonal算子的实现

利用迭代器，在一般情况下，我们只需要两层for循环，便可以实现Diagonal算子的计算过程。第一层for循环用于确定除dim1和dim2维度的位置坐标，第二层for循环用于对dim1和dim2对应维度确定对角元素位置，通过这样的两层for循环，便可将对角元素位置确定。通过这样的取值处理，相较于Eigen实现思路，计算速度有着明显的提升，且无维度限制，st测试结果对比如下：

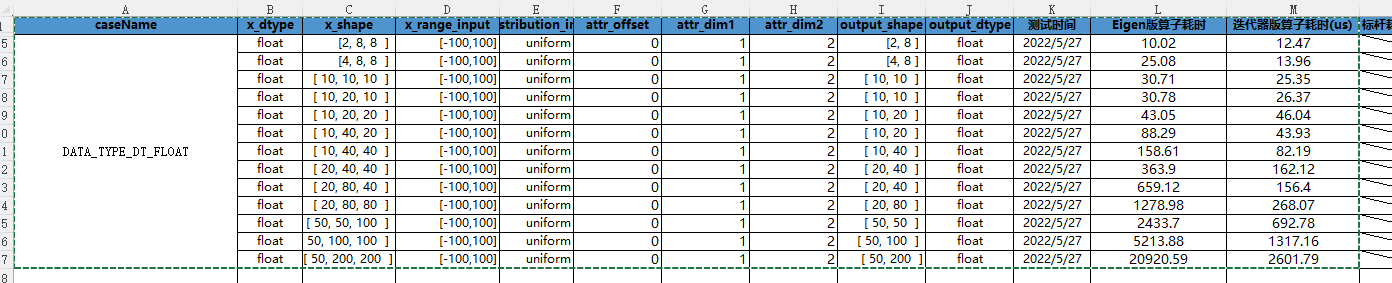
具体实现可参见如下代码：

template <typename T>
uint32_t DiagonalCpuKernel::DoComputeType(CpuKernelContext &ctx,
                                          const int64_t &offset,
                                          const int64_t &dim1,
                                          const int64_t &dim2) {
  // Get the inuput and output
  Tensor *input_x = ctx.Input(0);
  Tensor *y = ctx.Output(0);
  // Get some information of input
  auto x_shape = input_x->GetTensorShape();
  std::vector<int64_t> x_shape_ = x_shape->GetDimSizes();
  const int64_t x_dim = x_shape->GetDims();
  auto dataptr = reinterpret_cast<T *>(ctx.Input(0)->GetData());
  auto y_dataptr = reinterpret_cast<T *>(y->GetData());
  // Compute
  // 首先计算出对角线元素个数
  int64_t dsize = OffsetSize(offset, dim1, dim2, x_shape_);
  // 生成输入Tensor的步长向量x_stride
  std::vector<int64_t> x_stride = ConstructStride<int64_t>(x_shape_);
  // 分情况讨论，2维和大于2维的情况
  if (x_dim != N2) {
    //set the vx_shape and vx_stride
    // 生成x_shape和x_stride中除去dim1和dim2对应值的vx_shape与vx_stride
    std::vector<int64_t> vx_shape, vx_stride;
    for (unsigned int tmp_dim = 0; tmp_dim < x_shape_.size(); tmp_dim++) {
      if (tmp_dim != dim1 && tmp_dim != dim2) {
        vx_shape.push_back(x_shape_[tmp_dim]);
        vx_stride.push_back(x_stride[tmp_dim]);
      }
    }
    // set the y_shape, y_stride, vy_stride
    // 生成输出Tensor的形状及步长向量：y_shape和y_stride
    std::vector<int64_t> y_shape = vx_shape;
    y_shape.push_back(dsize);
    std::vector<int64_t> y_stride =
        ConstructStride<int64_t>(y_shape);
    // 生成输出Tensor的出去最后一维的步长向量：vy_stride
    std::vector<int64_t> vy_stride = y_stride;
    vy_stride.pop_back();
    // 读取对角数据
    std::vector<int64_t> v_start(vx_shape.size(), 0);
    for (PositionIterator<int64_t> myiter(v_start, vx_shape); !myiter.End();
         ++myiter) {
      // 利用迭代器确定除dim1和dim2维度的位置坐标
      auto p = myiter.GetPos();
      // 通过步长向量和位置坐标计算出输入和输出的基础位置值base_pos1和outbase_pos
      int64_t base_pos1 = MulSum<int64_t>(p, vx_stride);
      int64_t outbase_pos = MulSum<int64_t>(p, vy_stride);
      for (int i = 0; i < dsize; i++) {
      // 结合前面计算出的基础位置值，对dim1和dim2对应维度确定对角元素位置，并赋值给输出数据地址（get_data涉及对上对角还是下对角取元素，不影响对迭代器作用的理解）
        int64_t base_pos2 = i * (x_stride[dim1] + x_stride[dim2]);
        int64_t arr[N2] = {x_stride[dim1], x_stride[dim2]};
        y_dataptr[outbase_pos + i] =
            get_data(base_pos1 + base_pos2, offset, arr, dataptr);
      }
    }
  } else {
    for (int i = 0; i < dsize; i++) {
      int64_t base_pos = i * (x_stride[dim1] + x_stride[dim2]);
      int64_t arr[N2] = {x_stride[dim1], x_stride[dim2]};
      y_dataptr[i] = get_data(base_pos, offset, arr, dataptr);
    }
  }
  return KERNEL_STATUS_OK;
}

迭代器的其他用法

1、数据切条：如Sort算子中，用迭代器对Tensor数据关于tmp_axis维度进行取条，以进行后续的排序操作。

for (position_iterator<int64_t> mit(v_start, v_shape); !mit.end(); ++mit) {
      auto p = mit.get_pos();
      int axis_len = input_shape_[tmp_axis];
      std::vector<ValueIndex<T>> data_(axis_len);
      int base_pos = mul_sum<int64_t>(p, v_stride);
      for (int32_t i = 0; i < axis_len; i++) {
        data_[i].value = x_dataptr[base_pos + i * input_stride[tmp_axis]];
        data_[i].index = i;
      }

2、数据切块：切块处理可以利用两个迭代器循环叠加，也可以利用一个迭代器和两个坐标位置for循环

3、关于指定维度dim，对Tensor降维拆分为N子Tensor：如UniqueConsecutive算子中，首先需要关于属性axis维，将原本的Tensor数据拆分为input_shape[axis]个子Tensor（此处用vector存储Tensor中的数据）。

std::vector<std::vector<T1>> data_;
  for (int64_t i = 0; i < dim0; i++) {
    std::vector<T1> tmp_v1;
    for (PositionIterator<int64_t> mit(v_start, v_shape); !mit.End(); ++mit) {
      auto pos = mit.GetPos();
      tmp_v1.push_back(
          x_dataptr[MulSum<int64_t>(pos, v_stride) + i * input_stride[axis]]);
    }
    data_.push_back(tmp_v1);
  }

点击关注，第一时间了解华为云新鲜技术~