【python代码】 最大流问题+最小花费问题+python(ortool库)实现

目录

• 基本概念
  • 图
  • 邻接矩阵
  • 最大流问题
• python解决最大流问题
• python解决最大流最小费用问题

基本概念

图

定义： 图G(V,E)是指一个二元组(V(G),E(G))，其中:

1. V(G)={v1,v2,…, vn}是非空有限集，称为顶点集，
   
   2. E(G)是V(G)中的元素对(vi,vj)组成的集合称为边集。

---

举例：



V(G)={v1,v2,v3,v4}

E(G)= {e1,e2,e3,e4,e5,e6}

---

• 若图G的边是有方向的，称G是有向图，有向图的边称为有向边或弧。
• 与同一条边关联的两个端点称为相邻的顶点
• 与同一个顶点关联的两条边称为相邻的边
• 端点重合为一点的边称为环
• 若一对顶点之间有两条以上的边联结，则这些边称为重边．
• 既没有环也没有重边的图，称为简单图．
• 若图G的每一条边e 都赋以一个实数w(e)，称w(e)为边e的权， G连同边上的权称为赋权图 ,
• 图G的中顶点的个数， 称为图G的阶
• 图中与某个顶点相关联的边的数目，称为该顶点的度。
• 完全图：若无向图的任意两个顶点之间都存在着一条边，称此图为完全图。

邻接矩阵

• 以下均假设图为简单图，没有重边和环
• 图G的邻接矩阵是表示顶点之间相邻关系的矩阵
  
  

---

举个例子：

---

最大流问题

• 设G(V,E)为有向图，若在每条边e上定义一个非负权c， 则称图G为一个网络，称c为边e的容量函数，记为c(e)。

• 若在有向图G(V,E)中有两个不同的顶点vs与vt ，
  
  若顶点vs只有出度没有入度，称vs为图G的源，

• 若顶点vt只有入度没有出度， 称vt为G的汇，

• 若顶点v 既不是源也不是汇， 称为v中间顶点。

---

如图，就是从v1到v9怎么流动，在受每一个有向边的流动最大限制下，才是最大流。大学考试的内容一般都是用手算的，这里我们还是用python来解决最大流问题。

python解决最大流问题

from ortools.graph import pywrapgraph
start_nodes = [0, 0, 0, 1, 1, 2, 2, 3, 3]
end_nodes = [1, 2, 3, 2, 4, 3, 4, 2, 4]
capacities = [20, 30, 10, 40, 30, 10, 20, 5, 20]
max_flow = pywrapgraph.SimpleMaxFlow()
for i in range(0, len(start_nodes)):
    max_flow.AddArcWithCapacity(start_nodes[i], end_nodes[i], capacities[i])
# Find the maximum flow between node 0 and node 4.
if max_flow.Solve(0, 4) == max_flow.OPTIMAL:
    print('Max flow:', max_flow.OptimalFlow())
    print('')
    print('  Arc    Flow / Capacity')
    for i in range(max_flow.NumArcs()):
        print('%1s -> %1s   %3s  / %3s' % (
          max_flow.Tail(i),
          max_flow.Head(i),
          max_flow.Flow(i),
          max_flow.Capacity(i)))
    print('Source side min-cut:', max_flow.GetSourceSideMinCut())
    print('Sink side min-cut:', max_flow.GetSinkSideMinCut())
else:
    print('There was an issue with the max flow input.')

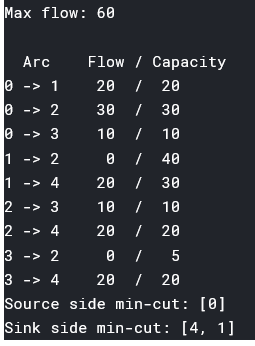
运行结果如下：

python解决最大流最小费用问题

跟最大流问题类似，但是每一条边多了一个费用的概念

• 从图中可以看到，0点生产了20个货物，然后要送5个到3，15个到4
• 一条边（15，4）意味着这个最多可以运输15个货物，每运输一个货物就要支付4点费用

from ortools.graph import pywrapgraph
#between each pair. For instance, the arc from node 0 to node 1 has acapacity of 15 and a unit cost of 4.
start_nodes = [ 0, 0,  1, 1,  1,  2, 2,  3, 4]
end_nodes   = [ 1, 2,  2, 3,  4,  3, 4,  4, 2]
capacities  = [15, 8, 20, 4, 10, 15, 4, 20, 5]
unit_costs  = [ 4, 4,  2, 2,  6,  1, 3,  2, 3]
# Define an array of supplies at each node.
supplies = [20, 0, 0, -5, -15]
# Instantiate a SimpleMinCostFlow solver.
min_cost_flow = pywrapgraph.SimpleMinCostFlow()
# Add each arc.
for i in range(0, len(start_nodes)):
    min_cost_flow.AddArcWithCapacityAndUnitCost(start_nodes[i], end_nodes[i],
                                                capacities[i], unit_costs[i])
# Add node supplies.
for i in range(0, len(supplies)):
    min_cost_flow.SetNodeSupply(i, supplies[i])
 # Find the minimum cost flow between node 0 and node 4.
if min_cost_flow.Solve() == min_cost_flow.OPTIMAL:
    print('Minimum cost:', min_cost_flow.OptimalCost())
    print('')
    print('  Arc    Flow / Capacity  Cost')
    for i in range(min_cost_flow.NumArcs()):
      cost = min_cost_flow.Flow(i) * min_cost_flow.UnitCost(i)
      print('%1s -> %1s   %3s  / %3s       %3s' % (
          min_cost_flow.Tail(i),
          min_cost_flow.Head(i),
          min_cost_flow.Flow(i),
          min_cost_flow.Capacity(i),
          cost))
else:
    print('There was an issue with the min cost flow input.')

运行结果：



参考：

ortool 官网