Adaboost原理及相关推导
提升思想
一个概念如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么,这个概率是强可学习的。一个概念如果存在一个多项式的学习算法能够学习它,并且学习的正确率仅比随机猜测略好,那么,这个概念是弱可学习的。强可学习与弱可学习是等价的。在学习中,如果已经发现了弱学习算法,那么是否能够将其提升为强学习算法呢?、
Adaboost
设训练数据集T={(x1,y1),(x2,y2),(xN,yN)},对数据集进行初始化训练数据的权重分布:
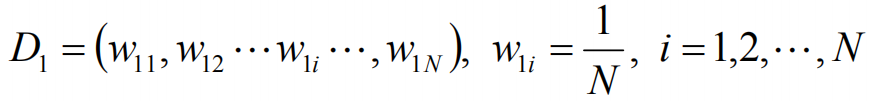
对于m=1,2,3······M,步骤如下:
使用具有权值分布Dm的训练数据集学习,得到基本分类器:

计算Gm(x)在训练数据集上的分类误差率:
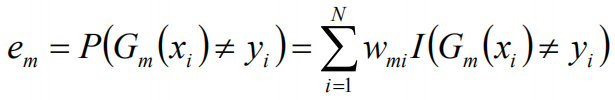
计算Gm(x)的系数:
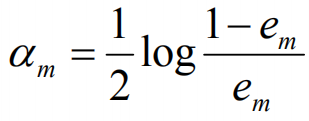
更新训练数据集的权值分布:
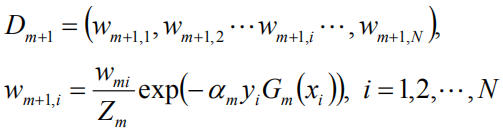
这里,Zm是规范化因子:
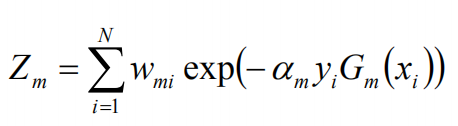
这里的规范化因子仅仅是要归一化。
基本分类器的线性组合
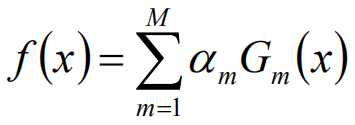
最终得到的分类器为:
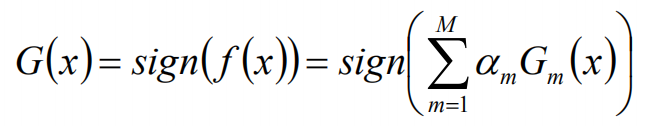
Adaboost中的误差上限
根据误差计算公式,有如下等式:
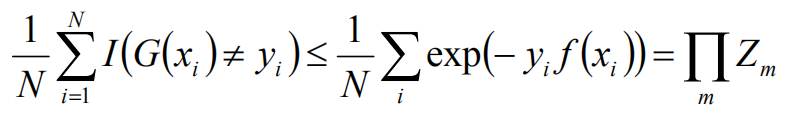
当G(xi)不等于yi时,yi*f(xi)<0,故exp(-yi*f(xi))>=1,前半部分得证,对于后面的等号,如下:
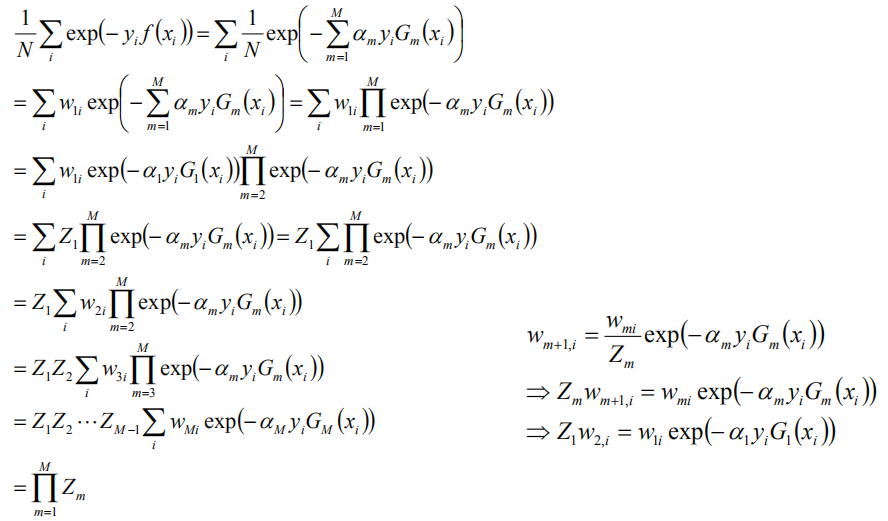
由此,可以计算得到训练的误差界,如下:
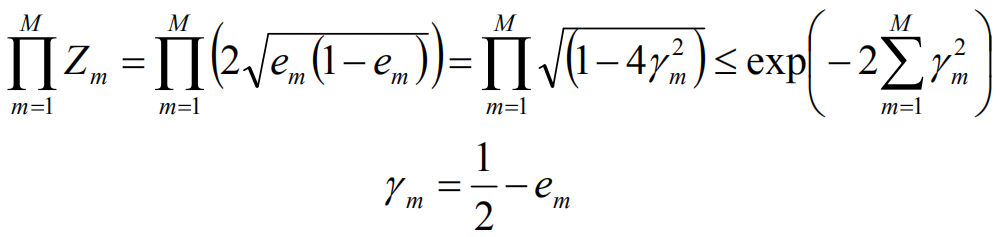
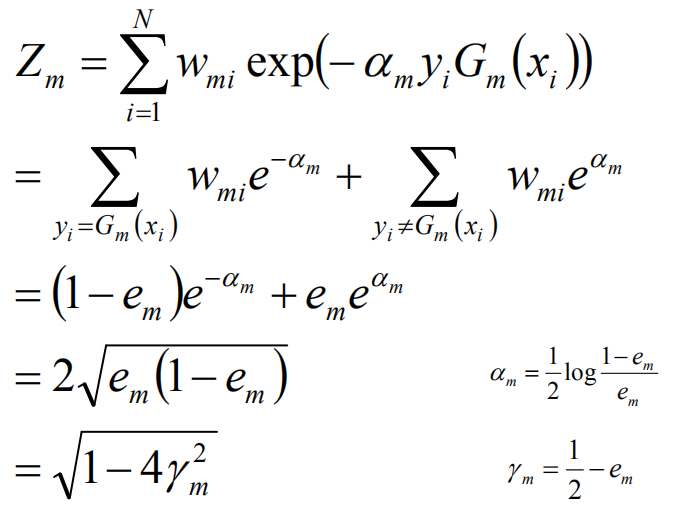
取r1,r2的最小值,记做r
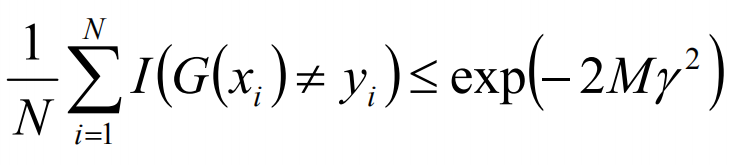
Adaboost算法解释
Adaboost算法是模型为加法模型,损失函数为指示函数,学习算法为前向分布算法时的二分类学习算法
前向分步算法
对于下面加法模型:
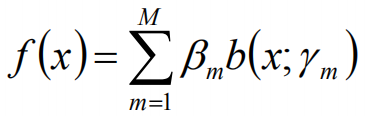
其中,b()函数为基函数,bm为基函数系数,rm为基函数的参数
前向分步算法在给定训练数据及损失函数L(y,f(x))的条件下,学习加法模型f(x)成为经验风险极小化,即损失函数极小化问题:
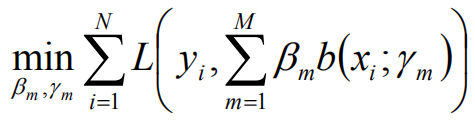
算法简化:如果能够从前向后,每一步只学习一个基函数及其系数,逐步逼近上式,即每一步只优化:
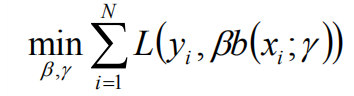
前向分布算法框架
输入:
训练数据集T,损失函数L(y,f(x)),基函数集{b(x;r)}\
输出:
加法模型f(x)
算法步骤:
初始化f0(x)=0
对于m=1,2,·······M
极小化损失损失函数:
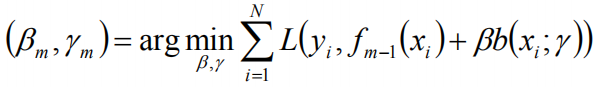
得到参数,b和r,在更新当前模型:
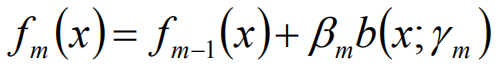
Adaboost算法是前向分布算法的特例,模型是由基本分类器组成的加法模型,损失函数是指数函数:
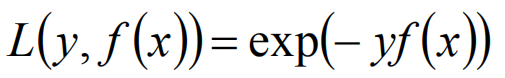
推导与证明
假设经过m-1轮迭代,前向分布算法已经得到fm-1(x):

在第m轮迭代得到am,Gm(x),fm(x),目标是使前向分布算法得到的am和Gm(x)使fm(x)在训练数据集T上的指数损失最小:
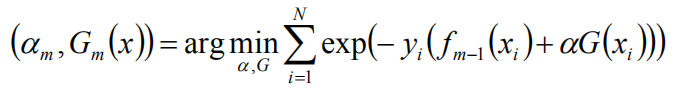
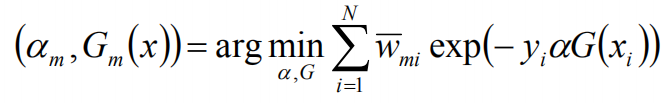
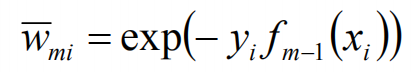
wmi既不依赖α也不依赖G,所以与最小化无关。但依赖于fm-1(x),所以,每轮迭代会发生变化。
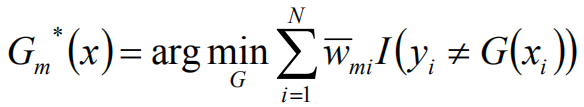
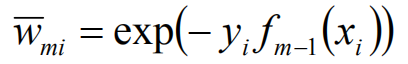
计算权值:
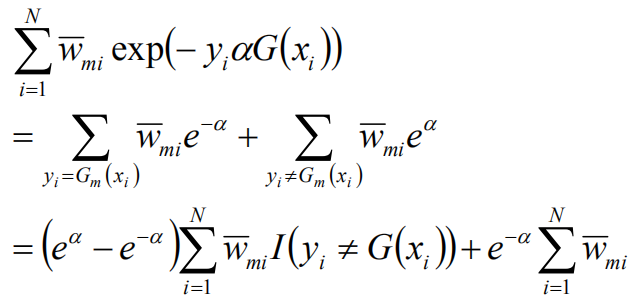
将G(x)带入
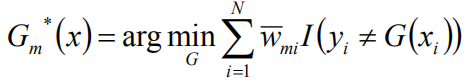
求导计算,得到:

分类错误率:
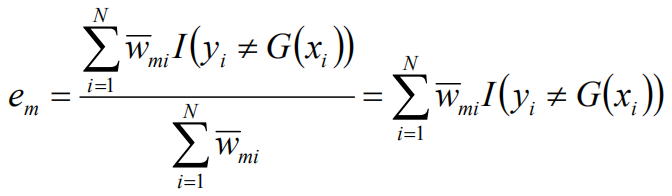
权值更新:
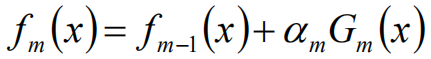
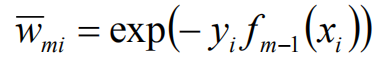
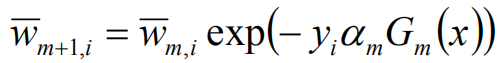
权值和错误率的关键解释:
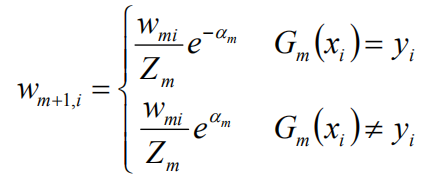
二者做除,得到:
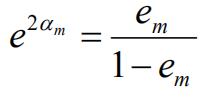
从而:
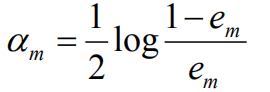
Adaboost原理及相关推导的更多相关文章
- AdaBoost原理详解
写一点自己理解的AdaBoost,然后再贴上面试过程中被问到的相关问题.按照以下目录展开. 当然,也可以去我的博客上看 Boosting提升算法 AdaBoost 原理理解 实例 算法流程 公式推导 ...
- 集成学习之Boosting —— AdaBoost原理
集成学习大致可分为两大类:Bagging和Boosting.Bagging一般使用强学习器,其个体学习器之间不存在强依赖关系,容易并行.Boosting则使用弱分类器,其个体学习器之间存在强依赖关系, ...
- 【Oracle 集群】ORACLE DATABASE 11G RAC 知识图文详细教程之RAC 工作原理和相关组件(三)
RAC 工作原理和相关组件(三) 概述:写下本文档的初衷和动力,来源于上篇的<oracle基本操作手册>.oracle基本操作手册是作者研一假期对oracle基础知识学习的汇总.然后形成体 ...
- Adaboost原理及目标检测中的应用
Adaboost原理及目标检测中的应用 whowhoha@outlook.com Adaboost原理 Adaboost(AdaptiveBoosting)是一种迭代算法,通过对训练集不断训练弱分类器 ...
- SSH深度历险(十一) AOP原理及相关概念学习+xml配置实例(对比注解方式的优缺点)
接上一篇 SSH深度历险(十) AOP原理及相关概念学习+AspectJ注解方式配置spring AOP,本篇我们主要是来学习使用配置XML实现AOP 本文采用强制的CGLB代理方式 Security ...
- SSH深度历险(十) AOP原理及相关概念学习+AspectJ注解方式配置spring AOP
AOP(Aspect Oriented Programming),是面向切面编程的技术.AOP基于IoC基础,是对OOP的有益补充. AOP之所以能得到广泛应用,主要是因为它将应用系统拆分分了2个部分 ...
- SpringBoot启动原理及相关流程
一.springboot启动原理及相关流程概览 springboot是基于spring的新型的轻量级框架,最厉害的地方当属自动配置.那我们就可以根据启动流程和相关原理来看看,如何实现传奇的自动配置 二 ...
- 机器学习之AdaBoost原理与代码实现
AdaBoost原理与代码实现 本文系作者原创,转载请注明出处: https://www.cnblogs.com/further-further-further/p/9642899.html 基本思路 ...
- 深度学习课程笔记(九)VAE 相关推导和应用
深度学习课程笔记(九)VAE 相关推导和应用 2018-07-10 22:18:03 Reference: 1. TensorFlow code: https://jmetzen.github.io/ ...
随机推荐
- docker中安装宝塔面板教程
本人电脑是win10,安装的virtualbox,装的centos7.2,在centos7.2装了docker,这个比较简单,网上一大堆教程,今天说一下装好了docker之后怎么在docker中安装面 ...
- redis实现排行榜思路
用redis的排序集合类型 sortset()实现排行榜 zadd();添加 ZREVRANGE();查看
- 文件包含漏洞(pikachu)
文件包含漏洞 在web后台开发中,程序员往往为了提高效率以及让代码看起来更加简洁,会使用'包含'函数功能,比如把一系列功能函数都写进function.php中,之后当某个文件需要调用的时候,就直接在文 ...
- diskpart 分区,挂载,和移除
list disk select disk 1 clean Create partition primary size=102400 active format quick list volume a ...
- 汇编 之 win10 下安装dosbox 和 MASM
所需工具链接: 链接:https://pan.baidu.com/s/1nenMsSdgEkeRKc6wh9DQRA 提取码:1r89 只需要以下两个工具 安装dosbox 和MASM步骤 (1)解压 ...
- c语言-----劫持自己02
在上一节 c语言-----劫持原理01 已经叙述了劫持原理,下边正式进入劫持实战 1. 需要实现的功能 在c语言中 system("notepad") 可以打开一个记事本 syst ...
- 热门云服务超87GB电子邮箱和密码泄露,黑客已验证大部分数据
热门云存储服务Mega被曝发现超87GB电子邮件地址和密码泄露(源数据目前已被删除,但已流传到个别黑客网站),其中包含近7.73亿电子邮件地址和2200万密码. 近日,国外一名安全研究人员Troy H ...
- Java Web:jstl处理字符串
用法:${fn:methodName(args....)} 在使用这些函数之前必须在JSP中引入标准函数的声明<%@ taglib prefix="fn" uri=" ...
- ajax学习摘抄笔记
2019独角兽企业重金招聘Python工程师标准>>> AJAX = Asynchronous JavaScript and XML(异步的 JavaScript 和 XML). A ...
- 图论--最长路--基于SPFA的调整模板
#include<iostream> #include<queue> #include<algorithm> #include<set> #includ ...
