java学习-循环结构-递归练习1-汉诺塔问题

相传在印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。
该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如下图)。
游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。
操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。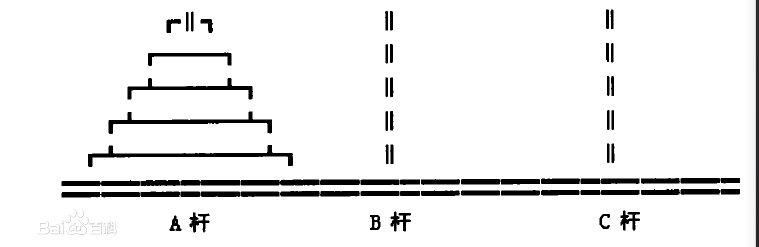

分析：对于这样一个问题，任何人都不可能直接写出移动盘子的每一步，但我们可以利用下面的方法来解决。

设移动盘子数为n，为了将这n个盘子从A杆移动到C杆，可以做以下三步：

 

(1)以C盘为中介，从A杆将1至n-1号盘移至B杆；

(2)将A杆中剩下的第n号盘移至C杆；

(3)以A杆为中介；从B杆将1至n-1号盘移至C杆。

import java.util.Scanner;
public class Hanoi {
    public static void main(String[] args) {
        System.out.println("请输入盘子数量：");
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();

        hanoi(n,"A","B","C");
    }

    /**
     *   将n个盘子从a柱借助b柱，移到c柱。
     * @param n  盘子的数量
     * @param a  A 柱子
     * @param b  B 柱子
     * @param c  C 柱子
     */
    private static void hanoi(int n, String a, String b, String c) {
　　　　　　　//递归最终会有一个终点，就是底值。这里n=1就是底值。
        if (n==1){
            System.out.printf("%s-->%s \n",a,c);
        }else {
            //1.将a柱上面的n-1从a柱借助于c柱移到b柱;
            hanoi(n-1,a,c,b);
            //2.将a柱最底下的盘子直接移到c柱;
            System.out.printf("%s-->%s \n",a,c);
            //3.将b柱上面的n-1个盘子借助于a柱移到c柱;
            hanoi(n-1,b,a,c);
        }
    }
}