访问官网https://openwrite.cn/注册登录

访问https://openwrite.cn/plugin-chrome/ 下载插件和安装插件"OpenWrite助手1.1.4"

访问https://my.openwrite.cn/chrome 选择插件检测



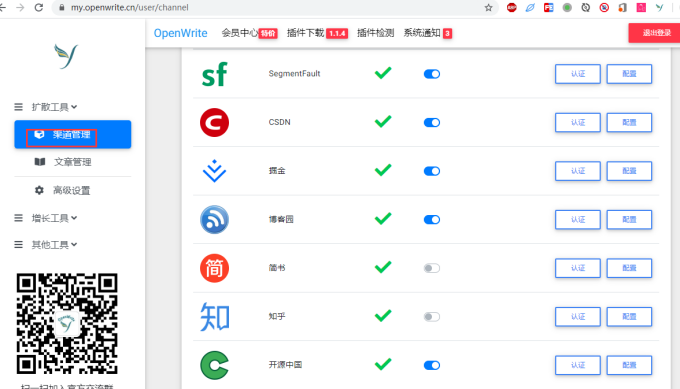
然后配置渠道管理,配置成功后就可以发送文章了



如果文章发送失败可以查看系统通知，查看失败的原因

本文由博客一文多发平台 OpenWrite 发布！

openwrite使用说明的更多相关文章

  1. Atitit.项目修改补丁打包工具 使用说明

    Atitit.项目修改补丁打包工具 使用说明 1.1. 打包工具已经在群里面.打包工具.bat1 1.2. 使用方法:放在项目主目录下,执行即可1 1.3. 打包工具的原理以及要打包的项目列表1 1. ...

  2. awk使用说明

    原文地址:http://www.cnblogs.com/verrion/p/awk_usage.html Awk使用说明 运维必须掌握的三剑客工具:grep(文件内容过滤器),sed(数据流处理器), ...

  3. “我爱背单词”beta版发布与使用说明

    我爱背单词BETA版本发布 第二轮迭代终于画上圆满句号,我们的“我爱背单词”beta版本已经发布. Beta版本说明 项目名称 我爱背单词 版本 Beta版 团队名称 北京航空航天大学计算机学院  拒 ...

  4. Oracle 中 union 和union all 的简单使用说明

    1.刚刚工作不久,经常接触oracle,但是对oracle很多东西都不是很熟.今天我们来了解一下union和union all的简单使用说明.Union(union all): 指令的目的是将两个 S ...

  5. Map工具系列-02-数据迁移工具使用说明

    所有cs端工具集成了一个工具面板 -打开(IE) Map工具系列-01-Map代码生成工具说明 Map工具系列-02-数据迁移工具使用说明 Map工具系列-03-代码生成BySQl工具使用说明 Map ...

  6. Map工具系列-03-代码生成BySQl工具使用说明

    所有cs端工具集成了一个工具面板 -打开(IE) Map工具系列-01-Map代码生成工具说明 Map工具系列-02-数据迁移工具使用说明 Map工具系列-03-代码生成BySQl工具使用说明 Map ...

  7. jQuery验证控件jquery.validate.js使用说明

    官网地址:http://bassistance.de/jquery-plugins/jquery-plugin-validation jQuery plugin: Validation 使用说明 转载 ...

  8. gdbsever 使用说明

    gdbsever 使用说明 在新塘N3292x平台下 编译 gdbsever ./configure --target=arm-linux --host=arm-linux arm-linux-gdb ...

  9. mongoVUE的增删改查操作使用说明

    mongoVUE的增删改查操作使用说明 一. 查询 1. 精确查询 1)右键点击集合名,再左键点击Find 或者直接点击工具栏上的Find 2)查询界面,包括四个区域 {Find}区,查询条件格式{& ...

随机推荐

  1. 1. postman使用

    postman使用教程: https://blog.csdn.net/fxbin123/article/details/80428216 http://bayescafe.com/tools/use- ...

  2. oracle数据库表用序列实现主键自增长

    原理注意:序列和触发器必须建立在同一个用户名下否则运行出错1.建立数据表create table 表名(           userid number(10) primary key,        ...

  3. 使用docker构建双主mysql

    我们有的时候需要双主mysql, 这样无论哪个数据库出现了问题的话都可以继续使用数据库.把两个数据库挂到一个代理上面,这样哪个服务出问题了,另外一个就可以继续服务了.当然本文不是主要谈代理的,所以这个 ...

  4. 从ISTIO熔断说起-轻舟网关熔断

    最近大家经常被熔断洗脑,股市的动荡,让熔断再次出现在大家眼前.微服务中的熔断即服务提供方在一定时间内,因为访问压力太大或依赖异常等原因,而出现异常返回或慢响应,熔断即停止该服务的访问,防止发生雪崩效应 ...

  5. 服务器模型---socket!!!

    /*********************服务器模型******************/ 一.循环服务器:循环服务器在同一时刻只可以相应一个客户端请求: 二.并发服务器:并发服务器在同一时刻可以相 ...

  6. imread()用法|| root权限

    1.ushort用法? USHORT is a macro which is not part of the official C++ language (it's probably defined ...

  7. Mysql性能优化：为什么你的count(*)这么慢？

    导读 在开发中一定会用到统计一张表的行数,比如一个交易系统,老板会让你每天生成一个报表,这些统计信息少不了 sql 中的count函数. 但是随着记录越来越多,查询的速度会越来越慢,为什么会这样呢?M ...

  8. WeChat-SmallProgram：自定义select下拉选项框组件

    1):创建组件所需的文件 2):自定义组件 CSS 及 JS 组件的wxml: <view class='com-selectBox'> <view class='com-sCont ...

  9. iOS 图片加载速度优化

    FastImageCache 是 Path 团队开发的一个开源库,用于提升图片的加载和渲染速度,让基于图片的列表滑动起来更顺畅,来看看它是怎么做的. 一.优化点 iOS 从磁盘加载一张图片,使用 UI ...

  10. PHP序列化及反序列化分析学习小结

    PHP反序列化 最近又遇到php反序列化,就顺便来做个总结. 0x01 PHP序列化和反序列化 php序列化:php对象 序列化的最主要的用处就是在传递和保存对象的时候,保证对象的完整性和可传递性.序 ...