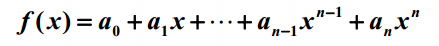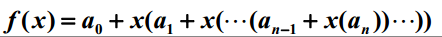数据结构-浙大 MOOC 笔记一 基本概念
做一些笔记记录自己的学习过程
第一节课介绍了数据结构的基本概念,首先没有直接给出相关的定义而是通过思考如何在书架上摆放书籍这样一个简单的类比了解到数据的组织方式的重要性,并通过printN函数的循环实现和递归实现的差异来说明解决问题方法的效率跟空间的利用效率有关,计算多项式在某一个给定点处的值来说明解决问题方法的效率与算法的设计有关。
void PrintN(int N)
{int i;
for (i=1;i<=N;i++){
printf("%d\n",i);
}
return;
} //循环实现
void PrintN (int N)
{
if (N){
PrintN(N-1);
printf("%d\n",N);
}
return;
} //递归实现
double f( int n, double a[], double x)
{ int i;
double p=a[];
for (i=; i<=n; i++)
p+= (a[i]* pow(x,i));
return p;
} //循环实现
double f( int n, double a[], double x)
{ int i;
double p= a[n];
for (i=n; i>; i--)
p = a[i-] + x*p;
return p;
} //递归实现
在进行算法分析和比较的过程中,我们会有实际进行程序运行时间的计算内容,这就需要用到clock()函数;
运行的模板如下
int main ()
start = clock();
MyFunction();
stop= clock();
duration = ((double) (stop= start)) / CLK_TCK
其中CLK_TCK 表示机器时钟每秒所走的时钟打点数
自然推导出相关的结论说明数据结构是关于 对象结构+操作+算法三个部分的内容
第一讲的最后又简单介绍了抽象数据类型的定义 (Abstract Data Type)
数据对象集 + 数据集合相关联的操作集
抽象表示实现方法不依赖于具体实现,under the hood部分的内容不做考虑,只关心开车不关心怎么造汽车的一个过程。
比如矩阵作为一种抽象数据类型
可以从以下几点来考虑

1.2 什么是算法?
- 有限的指令
- 接受一些输入
- 产生输出
- 在有限步骤之后终止
- 每一条指令必须 a.明确 b.计算机可处理 c.不依赖单独某一种特定的计算机语言
时间复杂度 与 空间复杂度的计算技巧
for 循环则相乘
if- else 取决于if条件判断复杂度和两个分枝部分的复杂度三者中的最大值
T1(n) + T2(n) = max
T1(n) * T2(n) = O (f1(n)*f2(n))
1.3 最大子列和问题-实例分析
算法1: 累加
for (i=; i<=n; i++){
ThisSum=;
for (j=i; j<=n; j++){
ThisSum+=A[j];
if (ThisSum> MaxSum)
MaxSum= ThisSum;
}
}
算法2: 分而治之
左 中 右

可以达到O(nlogn) 的时间复杂度
算法3: 在线处理
for (i=; i<N; i++) {
ThisSum+=A[i];
if (ThisSum> MaxSum)
MaxSum=ThisSum;
else if (ThisSum < )
ThisSum=;
}
根据“连续”条件作出的高效处理,如果是负数则直接舍弃,不做加和操作。
可以达到 O(n)的时间复杂度,遍历一次即可得到结果。
今天上完这门课程的第一讲,感觉课程内容还是比较简单清楚的,相比于学堂在线的MOOC数据结构,该课程难度会低一些,不过涉猎的范围会广一些,方便个人打基础。
数据结构-浙大 MOOC 笔记一 基本概念的更多相关文章
- 数据结构 浙大MOOC 笔记二 线性结构
线性表及其表现 第二章的内容是关于三种最基本的数据结构 结合<DDSA>第三章 表.栈和队列做一个总结 首先简单说明一下各个数据结构的特点: 数组:连续存储,遍历快且方便,长度固定,缺点是 ...
- JavaScript:学习笔记(2)——基本概念与数据类型
JavaScript:学习笔记(2)——基本概念与数据类型 语法 1.区分大小写.Test 和 test 是完全不同的两个变量. 2.语句最好以分号结束,也就是说不以分号结束也可以. 变量 1.JS的 ...
- Linux内核设计与实现笔记_1_基本概念
Linux内核设计与实现笔记_1_基本概念 操作系统 系统这个词包含了操作系统和所有运行在它上面的应用程序.操作系统是指在整个系统中负责完成分最基本功能和系统管理的那些部分,这些部分应该包括: 内核, ...
- 【阅读笔记】rocketmq 概念与架构 (一)
介绍 rocketmq 框架与基本概念 1. 概念 1.1 namesrv(name server) 记录了 broker 集群信息,消息队列的信息以及 key-value 配置,见 RouteInf ...
- 浙大MOOC《数据结构》随笔
第一讲 基本概念 1.1 什么是数据结构 图书摆放问题: 新书如何插入? 先定类别,再二分查找 怎么找到指定某本书? 二分查找 写程序实现一个函数PrintN 循环实现 void PrintN(int ...
- 数据结构入门第二课(浙大mooc)
数据结构入门第二课 目录 数据结构入门第二课 引子 多项式的表示 方法1 顺序结构表示多项式各项 方法2 顺序结构表示非零项 方法3 链表结构存储非零项 多项式问题的启示 线性表 线性表的抽象数据类型 ...
- ROS学习笔记2-基本概念
本笔记来源于:http://wiki.ros.org/ROS/Concepts ROS文件系统级别文件系统级别主要包含了你能在ROS的磁盘上遇到的资源,包括: 包(Packages):包是ROS中资源 ...
- linux设备树笔记__dts基本概念及语法【转】
转自:http://www.360doc.com/content/15/1113/11/15700426_512794532.shtml 设备树手册(Device Tree Usage)原文地址:ht ...
- es6学习笔记-class之一概念
前段时间复习了面向对象这一部分,其中提到在es6之前,Javasript是没有类的概念的,只从es6之后出现了类的概念和继承.于是乎,花时间学习一下class. 简介 JavaScript 语言中,生 ...
随机推荐
- ArrayIndexOutOfBoundsException
java.lang.ArrayIndexOutOfBoundsException: Array index out of range: 0 cusAndComs=this.getEm().create ...
- [LeetCode] Minimum Height Trees 最小高度树
For a undirected graph with tree characteristics, we can choose any node as the root. The result gra ...
- [LeetCode] Palindrome Permutation II 回文全排列之二
Given a string s, return all the palindromic permutations (without duplicates) of it. Return an empt ...
- css的字体
移动端使用的字体:http://www.cnblogs.com/PeunZhang/p/3592096.html
- JavaScript检测对象的类属性
function classof(o) { if(o === null) { return "Null"; } if(o === undefined) { return " ...
- 高介分类:核方法与支持向量机(SVM)
数据模型:并不是简单地二维数据,多个维度或者对象的数据聚合起来 { persion1's attr1:value1,...,persion1's attrN:va ...
- int[] convert byte[]
private void button_Click(object sender, RoutedEventArgs e) { byte[] bytes = this.ConvertIntArrayToB ...
- JS使用getComputedStyle()方法获取CSS属性值
在对网页进行调试的过程中,经常会用到js来获取元素的CSS样式,方法有很多很多,现在仅把我经常用的方法总结如下: 1. obj.style:这个方法只能JS只能获取写在html标签中的写在style属 ...
- c# treeview 基本知识
private void Form1_Load(object sender, EventArgs e) { BindTreeView(); treeView1.Focus(); treeView1.G ...
- decimal与double,float的选择与区别
decimal 类型可以精确地表示非常大或非常精确的小数.大至 1028(正或负)以及有效位数多达 28 位的数字可以作为 decimal类型存储而不失其精确性.该类型对于必须避免舍入错误的应用程序( ...