数据库实例: STOREBOOK > 用户 > 编辑 用户: SYSMAN

ylbtech-Oracle：数据库实例: STOREBOOK  >  用户  >  编辑 用户: SYSMAN

编辑 用户: SYSMAN

1. 一般信息返回顶部

1.1,

 

1.2,

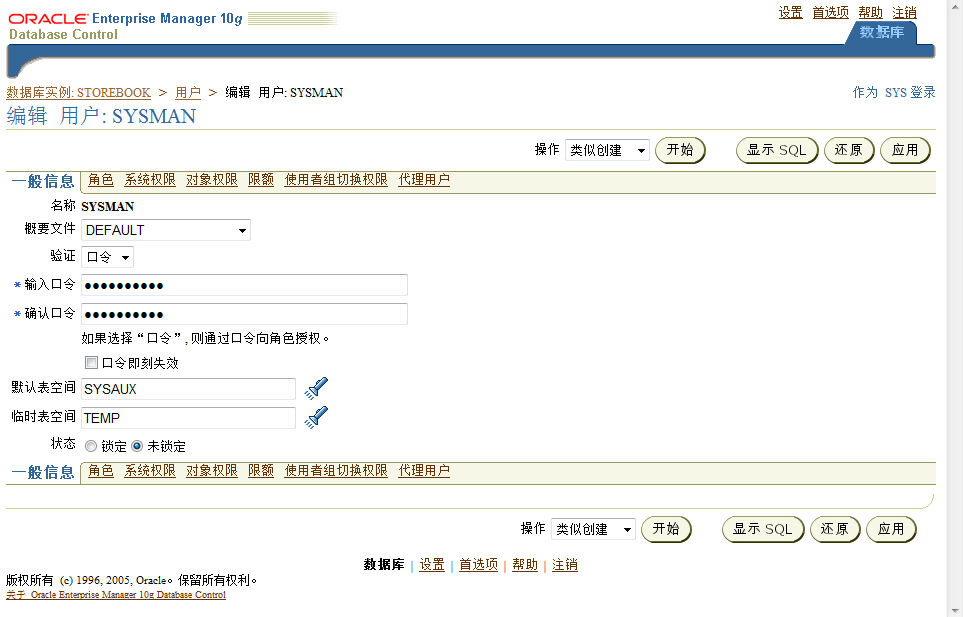
2. 角色返回顶部

2.1,

 

2.2,

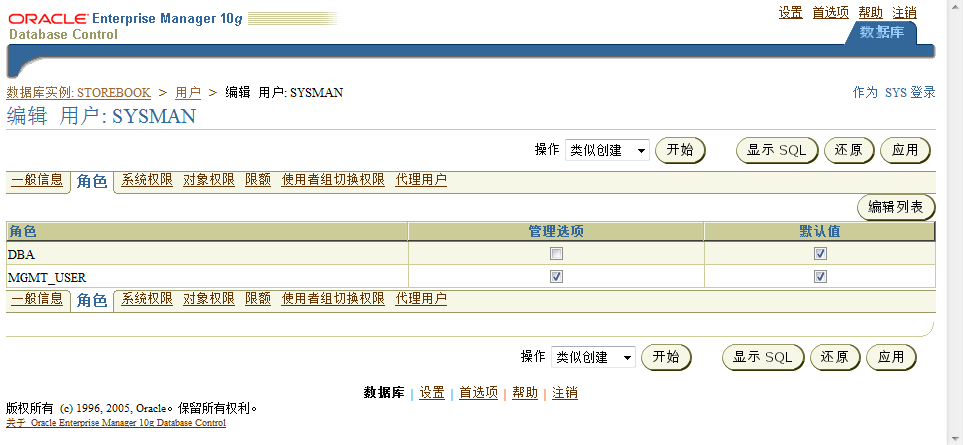
3. 系统权限返回顶部

3.1,

3.2,

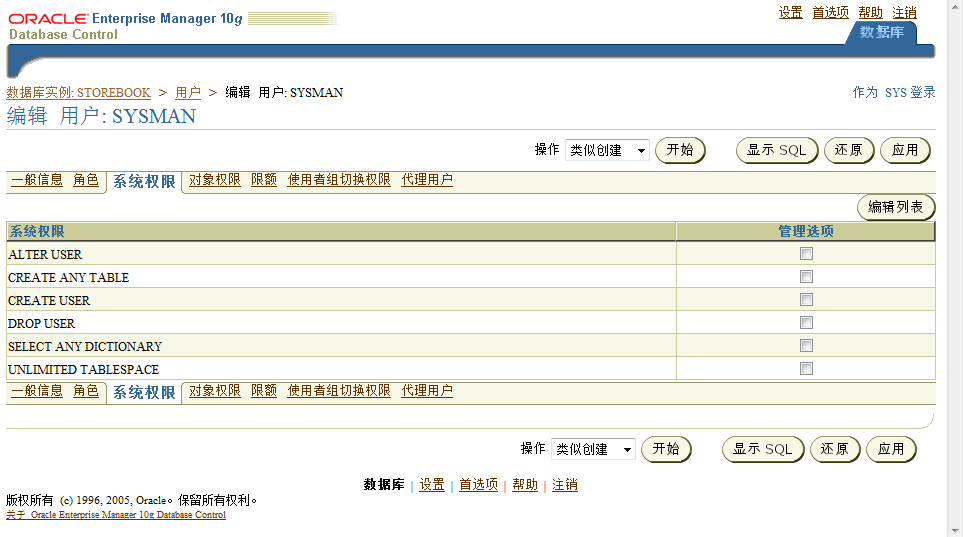
4. 对象权限返回顶部

4.1,

4.2,

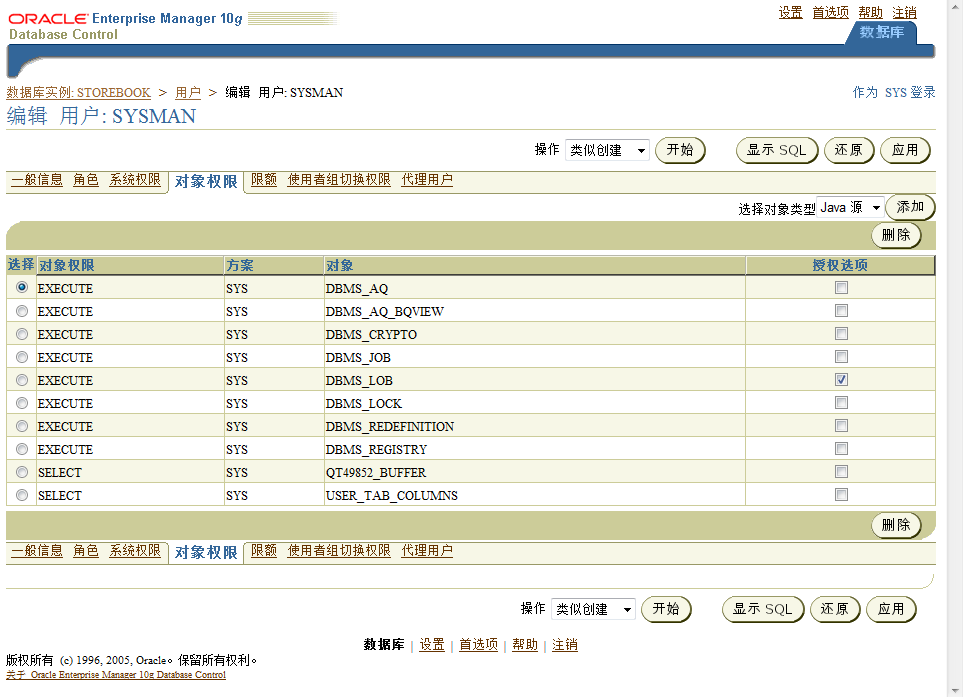
5. 限额返回顶部

5.1,

5.2,

 

6. 使用者组切换权限返回顶部

6.1,

6.2,

7. 代理用户返回顶部

7.1,

7.2,

8.返回顶部

8.1,

 

作者：ylbtech 出处：http://ylbtech.cnblogs.com/ 本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。