logistic回归算法及其matlib实现

一般来说，回归不用在分类问题上，因为回归是连续型模型，而且受噪声影响比较大。如果非要使用回归算法，可以使用logistic回归。

logistic回归本质上是线性回归，只是在特征到结果的映射中多加入了一层函数映射，即先把特征线性求和，然后使用函数g(z)作为假设函数来预测，g(z)可以将连续值映射到0和1上。

logistic回归的假设函数如下，线性回归假设函数只是\(\theta^Tx\)。

\[h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}\]

\[g(z)=\frac{1}{1+e^{-z}}\]

\[g’(z)=\frac{d}{dz}\frac{1}{1+e^{-z}}=\frac{1}{(1+e^{-z})^2}e^{-z}=\frac{1}{(1+e^{-z})}\bigg(1-\frac{1}{(1+e^{-z})}\bigg)=g(z)(1-g(z))\]

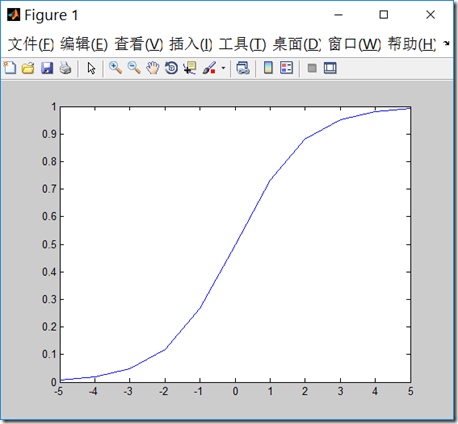
g函数一般称作logistic函数，图像如下，z很小时，g(z)趋于0，z很大时，g(z)趋于1，z=0时，g(z)=0.5

x = linspace(-5, 5, 11)

plot(x,1./(1+exp(-x)))

logistic回归用来分类0/1问题，也就是预测结果属于0或者1的二值分类问题。这里假设了二值满足伯努利分布，也就是

\[P(y=1|x;\theta)=h_\theta(x)\]

\[P(y=0|x;\theta)=1-h_\theta(x)\]

可以简写成：

\[p(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y}\]

参数的似然性：

\[L(\theta)=p(\vec{y}|X;\theta) = \prod_{i=1}^{m}p(y^{(i)}|x^{(i)};\theta)= \prod_{i=1}^{m}(h_\theta(x^{(i)}))^{y^{(i)}} (1-h_\theta(x^{(i)}))^{1-y^{(i)}} \]

求对数似然性：

\[l(\theta)=logL(\theta)=\sum\limits_{i=1}^{m}(y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))\]

为了使似然性最大化，类似于线性回归使用梯度下降的方法，求对数似然性对\(\theta\)的偏导，即：

\[\theta:=\theta+\alpha\bigtriangledown_{\theta}l(\theta)\]

因为求最大值，此时为梯度上升。

偏导数展开：

\begin{align*} \frac{\partial}{\partial\theta_j}l(\theta) &=\bigg(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)}\bigg)\frac{\partial}{\partial\theta_j}g(\theta^Tx) \\

&=\bigg(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)}\bigg)g(\theta^Tx)(1-g(\theta^Tx))\frac{\partial}{\partial\theta_j}\theta^Tx \\ &=\big(y(1-g(\theta^Tx)-(1-y)g(\theta^Tx)\big)x_j \\ &=(y-h_\theta(x))x_j
\end{align*}

则：

一个采样中计算\(\theta_j\)，随机梯度上升法

\[\theta_j:=\theta_j+\alpha(y^{(i)}-h_{\theta}(x^{(i)}))x_j^{(i)}\]

从所有采样中计算\(\theta_j\)，批量梯度上升法，这和我们前面推导的线性回归的梯度下降法公式是一致的。

\[\theta_j:=\theta_j+\alpha\frac{1}{m}\sum\limits_{i=1}^{m}(y^{(i)}-h_{\theta}(x^{(i)}))x_j^{(i)}\]

梯度上升法和梯度下降法是等价的，比如在上面公式推导中，可以令\(J(\theta)=-l(\theta)\),求导数后，得到梯度下降法的迭代公式

\[\theta_j:=\theta_j-\alpha(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}\]

数据下载：

http://openclassroom.stanford.edu/MainFolder/courses/MachineLearning/exercises/ex4materials/ex4Data.zip

ex4x.dat   第一列	ex4x.dat 第二列	ex4y.dat
成绩1分数	成绩2分数	是否被录取，1是，0否

和前面实现线性回归一样(http://www.cnblogs.com/mikewolf2002/p/7634571.html)，我们也可以用矩阵来实现批量梯度上升法(或下降法)的迭代求解。

\[\theta_j:=\theta_j+\alpha\frac{1}{m}\sum\limits_{i=1}^{m}(y^{(i)}-h_{\theta}(x^{(i)}))x_j^{(i)}\]

对上面的公式，可以转化为矩阵，在matlib中，大致如下：\(A=\theta^Tx\),其中，\(x\)是\(m\times (n+1)\)维矩阵，\(m\)是样本数，\(n\)是特征数目，\(x\)中我们额外增加了1列，以便和\(\theta_0\)对应。

\(\theta\)是\((n+1)\times 1\)矩阵，则\(A\)为是\(m\times 1\)矩阵，然后\(x\)的转置再点乘以\((g(A)-y)\)得到梯度，最后乘以学习率\(\alpha\times\frac{1}{m}\),其中g表示logistic函数。

A = x*theta;
grad = (1/m).* x' * (g(A) - y);%求出梯度
theta = theta - alpha .* grad;%更新theta

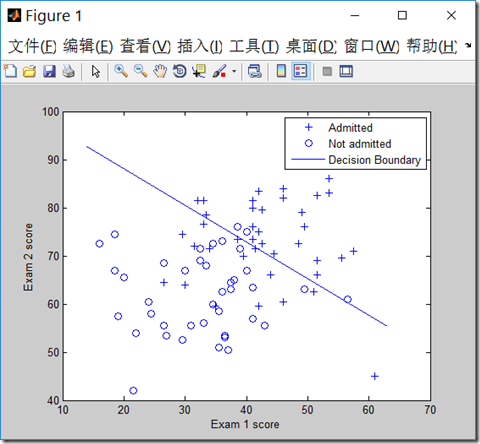
代码：

clear all; close all; clc

x = load('ex4x.dat');
y = load('ex4y.dat');

[m, n] = size(x);
x = [ones(m, 1), x]; % 输入特征增加一列，x0=1

figure
pos = find(y); neg = find(y == 0);%find是找到的一个向量，其结果是find函数括号值为真时的值的行号
plot(x(pos, 2), x(pos,3), '+')
hold on
plot(x(neg, 2), x(neg, 3), 'o')
hold on
xlabel('Exam 1 score')
ylabel('Exam 2 score')

theta = zeros(n+1, 1);%初始化theta值
g = inline('1.0 ./ (1.0 + exp(-z))'); %定义logistic函数
MAX_ITR = 605000;%最大迭代数目
alpha = 0.1; %学习率
i = 0;
while(i<MAX_ITR)
   A = x*theta;
   grad = (1/m).* x' * (g(A) - y);%求出梯度
   theta = theta - alpha .* grad;%更新theta
   if(i>2)
       delta = old_theta-theta;
       delta_v = delta.*delta;
       if(delta_v<0.0000001)%如果两次theta的内积变化很小，退出迭代
           break;
       end
       %delta_v
   end
   old_theta = theta;
   %theta
   i=i+1;
end
i
old_theta
theta
%theta=[-16.378;0.1483;0.1589];
prob =  g([1, 80, 80]*theta)
plot_x = [min(x(:,2))-2,  max(x(:,2))+2];
% 画出概率g(theta^Tx)=0.5的分界线,解出对应的theta值
plot_y = (-1./theta(3)).*(theta(2).*plot_x +theta(1));
plot(plot_x, plot_y)
legend('Admitted', 'Not admitted', 'Decision Boundary')

我们也可以用牛顿迭代法实现logistica回归。牛顿迭代法原理见：http://www.cnblogs.com/mikewolf2002/p/7642989.html

我们要求\(l’(\theta)=0\)时候的偏导数，换成牛顿迭代公式则为：

\[\theta := \theta - \frac{l'(\theta)}{l''(\theta)}\]

\[\theta := \theta - H^{-1}\bigtriangledown_{\theta}l(\theta)\]

其中\(\bigtriangledown_{\theta}l(\theta)\)为目标函数的梯度。\(H\)为Hessian矩阵，规模是\(n\times n\),\(n\)是特征的数量，它的每个元素表示一个二阶导数。

上述公式的意义就是，用一个一阶导数的向量乘以一个二阶导数矩阵的逆。优点：若特征数和样本数合理，牛顿方法的迭代次数比梯度上升要少得多。缺点：每次迭代都要重新计算Hessian矩阵，如果特征很多，则H矩阵计算代价很大。

\[H_{ij}=\frac{\partial^2l(\theta)}{\partial\theta_i\partial\theta_j}\]

\[H=X^T\begin{bmatrix}
g(\mathbf{x}_1)\cdot [1-g(\mathbf{x}_1)]&0&\cdots&0 \\

0&g(\mathbf{x}_2)\cdot [1-g(\mathbf{x}_2)]&\cdots&0 \\

\vdots & \vdots & \ddots & \vdots\\

0&0&\cdots&g(\mathbf{x}_m)\cdot [1-g(\mathbf{x}_m)] \\

\end{bmatrix}X\]

推导看这儿：牛顿法解机器学习中的Logistic回归

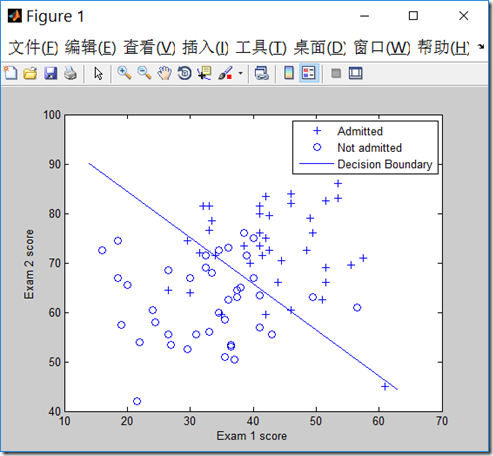
代码：

clear all; close all; clc

x = load('ex4x.dat');
y = load('ex4y.dat');

[m, n] = size(x);
x = [ones(m, 1), x]; % 输入特征增加一列，x0=1

figure
pos = find(y); neg = find(y == 0);%find是找到的一个向量，其结果是find函数括号值为真时的值的行号
plot(x(pos, 2), x(pos,3), '+')
hold on
plot(x(neg, 2), x(neg, 3), 'o')
hold on
xlabel('Exam 1 score')
ylabel('Exam 2 score')

theta = zeros(n+1, 1);%初始化theta值
g = inline('1.0 ./ (1.0 + exp(-z))'); %定义logistic函数

% Newton's method
MAX_ITR = 7;
J = zeros(MAX_ITR, 1);

for i = 1:MAX_ITR
    % Calculate the hypothesis function
    z = x * theta;
    h = g(z);%转换成logistic函数

    % Calculate gradient and hessian.
    % The formulas below are equivalent to the summation formulas
    % given in the lecture videos.
    grad = (1/m).*x' * (h-y);%梯度的矢量表示法
    %diag(h),返回向量h为对角线元素的方阵
    H = (1/m).*x' * diag(h) * diag(1-h) * x;%hessian矩阵的矢量表示法

    % Calculate J (for testing convergence)
    J(i) =(1/m)*sum(-y.*log(h) - (1-y).*log(1-h));%损失函数的矢量表示法

    theta = theta - H\grad;%H\逆矩阵
end
% Display theta
theta

% Calculate the probability that a student with
% Score 20 on exam 1 and score 80 on exam 2
% will not be admitted
prob = 1 - g([1, 20, 80]*theta)

%画出分界面
% Plot Newton's method result
% Only need 2 points to define a line, so choose two endpoints
plot_x = [min(x(:,2))-2,  max(x(:,2))+2];
% 画出概率g(theta^Tx)=0.5的分界线,解出对应的theta值
plot_y = (-1./theta(3)).*(theta(2).*plot_x +theta(1));
plot(plot_x, plot_y)
legend('Admitted', 'Not admitted', 'Decision Boundary')
hold off

% Plot J
figure
plot(0:MAX_ITR-1, J, 'o--', 'MarkerFaceColor', 'r', 'MarkerSize', 8)
xlabel('Iteration'); ylabel('J')
% Display J
J